Optellen of Vermenigvuldigen?

© h.hofstede (h.hofstede@hogeland.nl)
Uit de vaas hiernaast trekken we een bal, en stellen ons vooraf de vraag:

"Hoe groot is de kans dat de bal oranje is óf een cijfer minder dan 5 heeft?""

Makkelijk te beantwoorden natuurlijk:

Er zijn 5 gunstige mogelijkheden en 7 mogelijkheden in totaal, dus de kans is  5/7.
Die 5 gunstigen zijn afkomstig van 3 oranje ballen en van 2 ballen lager dan 5.
De kans op een oranje bal is 3/7  en op een bal lager dan 5 is de kans  2/7
Dat geeft totale kans  3/7 + 2/7 = 5/7.  Het lijkt erop dat we een nieuwe regel hebben gevonden:
P(A óf B) = P(A)  + P(B)
Maar pas op! Die regel klopt niet altijd. Lang niet altijd.....
Stel dat we een andere vraag hadden gesteld:

"Hoe groot is de kans dat de bal groen is óf meer dan 7?"

Dan hadden we met onze regel gevonden  P(groen) = 4/7  en  P(meer dan 7) = 3/7  dus  P(groen óf meer dan 7) = 4/7 + 3/7 = 1.  Dat is duidelijk onzin! Je kunt immers ook de oranje bal met 6 pakken!!  De werkelijke kans moet gelijk zijn aan 6/7, dat zie je wel als je gewoon de gunstige mogelijkheden bekijkt zonder onze "slimme" regel te gebruiken.

Waar is het fout gegaan?
Dat zie je als je de gunstige mogelijkheden opschrijft.
De groenen zijn de ballen  1,3,5,9  en meer dan 7 zijn de ballen 8, 9, 11. Dat zijn inderdaad 7 gunstige mogelijkheden. Hoe kan dat?  We hebben bal met nummer 9 dubbel meegeteld!  Die is namelijk  groen én meer dan 7.
Kortom:  onze regel is goed als de gebeurtenissen niet "overlappen", maar als dat wel zo is, dan moeten we de dubbel getelden er nog aftrekken.
De goede regel is de volgende:

P(A óf B)  =  P(A) + P(B) - P(A én B)
In dit laatste geval zou dat geven  4/3 + 3/7 - 1/7 = 6/7  en dat klopt inderdaad wél.
Die laatste P(A én B) is dus alleen nodig als de gebeurtenissen A en B overlappen. Als ze dat niet doen is deze kans gewoon nul.
   
  OPGAVEN
1. Kies een willekeurig geheel getal groter dan 0 en kleiner of gelijk aan 1000.
Hoe groot is de kans dat dit getal deelbaar is door 4 óf door 25?

0,28
   
2. Ik pak uit een doos met schaakstukken willekeurig een stuk.
Hoe groot is de kans dat dit zwart is óf een pion?

24/32
   
3. Als je 5 muntstukken op tafel gooit is de kans op precies 3 keer KOP gelijk aan 0,3125.
Hoe groot is de kans op 3 keer KOP óf 2 keer KOP?

0,625
   
4. In een portemonnee zitten 12 briefjes;  11 van 10 euro en 1 van 50 euro. Ik haal er willekeurig 3 briefjes uit. Elk van die drie briefjes heeft natuurlijk een even grote kans om het briefje van 50 euro te zijn.
Hoe groot is de kans dat de eerste 50 euro is óf de tweede óf de derde?

3/12
   
5. Op onze school  heerst een griepepidemie. 30% van de leerlingen is ziek! Van de meisjes is 25% ziek. Van alle leerlingen is 45% een jongen. Hoe groot is de kans dat een willekeurig gekozen leerling ziek is óf een meisje?

0,7125
       
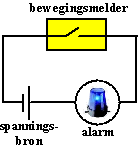
6. Hiernaast zie je een schets van een alarmsysteem.
Als de bewegingsmelder beweging detecteert, dan sluit de schakelaar en gaat er stroom door de kring lopen zodat het alarm afgaat.

Nou is zo'n bewegingsmelder niet helemaal  betrouwbaar.
Er zijn twee  mogelijke fouten die kunnen optreden.

Als eerste  kan de melder soms afgaan terwijl er veel te weinig beweging plaatsvindt. Dat is vervelend, want je wilt natuurlijk niet dat bij elke passerende bromvlieg het alarm afgaat.
De kans dat zoiets gebeurt is 6%.

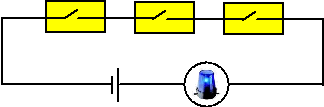
  Een oplossing is om meerdere melders in serie achter elkaar te schakelen. Hieronder zie je dat voor drie melders gedaan.
       
 

       
  a. Hoe groot is nu de kans dat het alarmsysteem een ongewenst alarm geeft?
       

0,000216
  b. Hoeveel zulke bewegingsmelder zou je in een alarmsysteem achter elkaar moeten schakelen zodat de kans op een ongewenst alarm minder dan één miljoenste wordt?
       

5
         
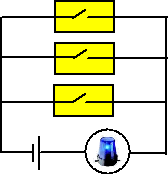
  De tweede fout die op kan treden is, dat de bewegingsmelder NIET reageert terwijl dat wel zou moeten. De kans daarop is 0,08.

Een oplossing daartegen is om meerdere meters parallel te schakelen, zoals hiernaast met drie meters is gedaan.

     
  c. Hoe groot is nu de kans dat het alarmsysteem niet reageert als dat wel zou moeten?
       

0,000512
  d. Hoe groot is nu de kans dat het alarmsysteem een ongewenst alarm geeft? 
       

0,18
 

         
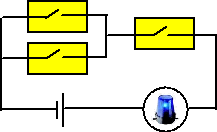
  e. Bepaal van het alarmsysteem hierboven de kans op een ongewenst alarm en ook de kans dat het alarm niet afgaat terwijl dat wel zou moeten.
       

0,0072
0,0864
       
7. examenvraagstuk HAVO Wiskunde A, 1994.
In de biologie komen we het begrip 'diversiteit' tegen. De diversiteit is een getal dat iets zegt over spreiding van soorten. Het begrip wordt niet alleen in de vrije natuur gehanteerd.
Een viskweker heeft een aantal vijvers met daarin verschillende soorten siervissen. Hoe zijn de vijvers samengesteld? De eenvoudigste manier is het tellen van het aantal verschillende soorten. In vijver 1 en 2 zitten slechts de gewone goudvis en de sluierstaart, en wel in onderstaande verhoudingen.
         
 
  vijver 1 vijver 2
gewone goudvis 90% 50%
sluierstaart 10% 50%
         
  Omdat vijver 1 grotendeels gevuld is met de gewone goudvis. terwijl de twee vissoorten in vijver 2 gelijk verdeeld zijn zou je vijver 2 'gemengder' kunnen noemen dan vijver 1. De vakterm voor 'gemengdheid' is diversiteit.
Simpson gebruikte de kansrekening om diversiteit van een populatie vast te leggen. Hij stelde zich voor dat je met teruglegging willekeurig twee keer een exemplaar kiest. De diversiteit (Div) van de populatie definieerde hij als de kans dat die twee exemplaren van verschillende soort zijn.
         
  a. Laat met een berekening zien dat Div voor vijver 1 kleiner is dan voor vijver 2.
         
  Hieronder is af te lezen hoe de vijvers 3 en 4 zijn samengesteld:
   
 
  vijver 3 vijver 4
gewone goudvis
sluierstaart
hemelkijker
leeuwekopgoudvis		 30%
30%
20%
20%		 30%
0%
50%
20%
         
  b. Bereken Div van vijver 4.    
       

0,62
  Een kweker berekent dat de Div van vijver 3 precies gelijk is aan 0,74. Bij deze vijver is de diversiteit al bijna maximaal. De maximale waarde wordt bereikt als er van elke soort evenveel exemplaren aanwezig zijn.
         
  c. Controleer met een berekening dat de maximale diversiteit bij vier soorten gelijk is aan 0,75.
         
  d. De maximale waarde van Div hangt af van het aantal soorten. Stel dat in een vijver n verschillende soorten zitten. Geef dan een formule voor de maximale Div uitgedrukt in n.
       

1 - 1/n
8. examenvraagstuk HAVO wiskunde A, 1991.
       
  Bij een ingewikkeld apparaat is vaak een keten van onderdelen nodig om het geheel te laten functioneren. Daarbij is de betrouwbaarheid van een keten (zoals in de figuur hieronder) kleiner dan de betrouwbaarheid van de afzonderlijk delen. Dat komt doordat het uitvallen van één onderdeel het uitvallen van de hele keten tot gevolg heeft.
Bekijk een keten van 5 onderdelen (A, B, C, D en E), die elk een kans van 10% hebben om uit te vallen, of, wat hetzelfde is, die elk een betrouwbaarheid hebben van 90%.
       
 

       
  a. Laat zien dat de betrouwbaarheid van deze keten ongeveer 60% is.
       
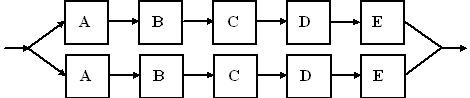
  Men kan de betrouwbaarheid vergroten door naast de keten van de figuur hierboven een zelfde keten te schakelen (zie onderstaande figuur). Dit heeft het voordeel dat als één keten uitvalt het systeem nog blijft functioneren.
       
 

         
  b. Bereken de betrouwbaarheid van dit tweede systeem.
         
  Een nog beter systeem krijgt men door de 10 onderdelen zo te schakelen als hieronder weergegeven is.
         
 

         
  Elk van de tien onderdelen heeft weer een betrouwbaarheid van 90%
         
  c. Bereken de betrouwbaarheid van dit laatste systeem.
         
 

© h.hofstede (h.hofstede@hogeland.nl)