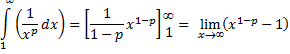© h.hofstede (h.hofstede@hogeland.nl)

       
1. a.  
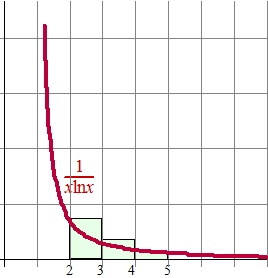
    bij het primitiveren is gebruik gemaakt van het feit dat 1/x de afgeleide is van lnx

Je ziet dat die blokjes hiernaast boven de grafiek blijven, dus een grotere totale oppervlakte hebben.

De som zal dus divergeren.
 
       
  b.  
       
    bij het primitiveren is gebruik gemaakt van het feit dat x  ongeveer de afgeleide is van -x2
De integraal convergeert dus de som ook
       
  c.
       
    De integraal divergeert dus de som ook  
       
2. Neem uiteraard  f(x) = 1/xp  , die dalend en continu is op interval   [1, →〉
Het geval p = 1 hebben we in de les al besproken:  de integraal wordt oneindig.
Neem p > 1:
 

  Als p > 1  dan is  1 - p < 0  en dan gaat  x1 - p   naar  0  als x naar oneindig gaat.
Dus er is convergentie voor p > 1.
       
       

© h.hofstede (h.hofstede@hogeland.nl)