 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| De
hoek tussen een lijn en een vlak. |
|
|
Het probleem van de hoek tussen
een lijn en een vlak is: welke hoek moet je nemen? Er zijn er zo
veel!!!
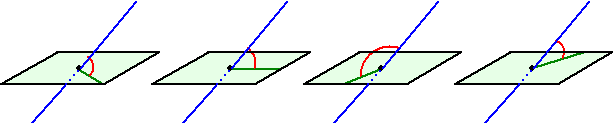
Kijk hieronder maar: allemaal hoeken tussen de lijn en het vlak en
allemaal verschillend!! Is er soms niet zoiets als DE hoek tussen een
lijn en een vlak? |
|
|
|
|
|
|
| Hier staat vier keer de hoek
tussen de gegeven blauwe lijn en een andere lijn uit het groene vlak.
Maar zo kun je wel oneindig veel groene lijnen in dat vlak tekenen. Kijk
maar hiernaast. Welke geeft de goede hoek? Is één van die groene
lijnen hiernaast specialer dan de anderen?
Het antwoord komt vanzelf als we de zaak wat beter belichten.
Letterlijk in dit geval.....
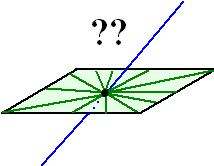
Laten we een lamp boven het vlak zetten, en de rest van het licht in de kamer
uitdoen: |
|
|
|
|
|
Neem aan dat de lichtstralen van
de lamp allemaal loodrecht op het vlak staan.
Zie je al welke van de groene lijnen een aparte is?
Als je goed kijkt dan zie je op het vlak ook de schaduw van
de blauwe lijn.
Er is precies één groene lijn die precies die schaduwlijn volgt, en
die gaan we nemen. Zo'n schaduwlijn noemen we de projectie
van de lijn op het vlak.
|
|
Hoek tussen lijn en
vlak
=
Hoek tussen de lijn en zijn projectie |
|
|
|
|
|
| Hoe werkt
dat in praktijk? |
|
|
|
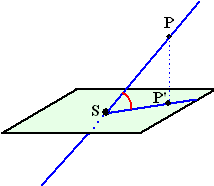
Als je de hoek tussen een lijn en
een vlak moet bepalen, dan bepaal je eerst het snijpunt S van de lijn
met het vlak.
Daarna kies je een willekeurig punt P van de lijn en je bepaalt de
loodrechte projectie (P') van P op het vlak
De gevraagde hoek is nu hoek PSP' .
Je moet eigenlijk het plaatje hiernaast in je hoofd hebben....
Lijkt simpel, maar het lastigst zal worden om punt P' te vinden.
Vooral als het vlak "scheef" ligt is het soms moeilijk te zien
hoe je loodrecht van punt P naar het vlak toe moet gaan. |
|
|
|
| Uitgebreid Voorbeeld. |
|
|
|
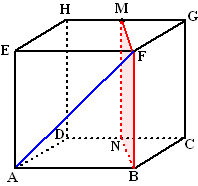
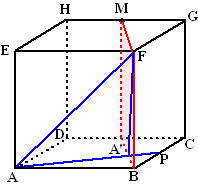
Hiernaast staat een kubus ABCD.EFGH
met ribben 4.
Bereken de hoek tussen lijn AF en vlak MNBF waarbij M en N de middens
van HG en DC zijn.
Het snijpunt S van de lijn met het vlak is in dit geval punt F, dus
dáár zit die hoek.
Als willekeurig punt P van de lijn kun je waarschijnlijk het best punt A
nemen, en dan komt de vraag: "Hoe ga je van punt A loodrecht
naar vlak MNBF?"
Dat is zo als de lijn die je tekent maar loodrecht staat op TWEE lijnen
uit dat vlak. |
|
| Als je in de figuur hiernaast van A in het
grondvlak naar het vlak toe gaat, dan staat die lijn in iedere geval
loodrecht op MN en FB. |
|
Als je nou zorgt dat hij óók
nog loodrecht op NB staat dan staat hij dus loodrecht op het hele vlak.
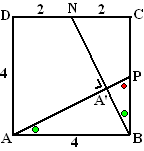
Teken daarom het grondvlak ABCD plat.
Zorg in de figuur hiernaast dat de groene hoeken gelijk zijn. Dan is de
rode hoek plus de groene hoek 90º (kun je zien in driehoek ABP).
Maar dan is in BA'P de groene plus de rode óók 90º, dus is de derde
hoek ook 90º, dus staan AP en BN loodrecht op elkaar.
Uit symmetrie van de figuur zie je dat P het midden van BC moet zijn. |
|
Met Pythagoras bereken je dat AP
= √20.
Uit de gelijkvormigheid van AA'B en ABP volgt dan eenvoudig dat:
AA'/AB = AB/AP
dus AA' = AB • AB/AP = 4 • 4/√20
= 16/√20.
Hiernaast zie je dat dan voor de gevraagde hoek AFA' geldt, dat
sin(AFA') = AA'/AF = 16/√20/√32
en daaruit volgt weer dat de hoek ongeveer gelijk is aan 39,2º. |
|
| |
|
|
OPGAVEN |
|
|
| 1. |
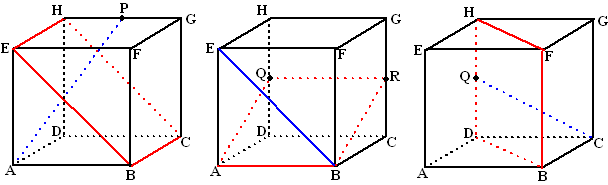
Hieronder staat drie keer een kubus
ABCD.EFGH getekend. De lengte van de ribben doet er niet toe.
Neem maar wat. P, Q en R zijn de middens van
respectievelijk HG, HD en GC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a. |
Bereken de hoek tussen AP en vlak EBCH. |
|
|
b. |
Bereken de hoek tussen EB en vlak ABRQ. |
|
|
c. |
Bereken de hoek tussen CQ en
vlak BDHF. |
|
|
|
|
|
|
|
| 2. |
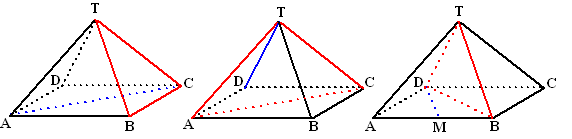
Hieronder staat drie keer een
regelmatige vierzijdige piramide waarvan alle ribben lengte 4
hebben. |
|
|
|
|
|
|
|
|
|
|
|
 a. a. |
Bereken de hoek tussen vlak TBC en
lijn AC. |
|
|
b. |
Bereken de hoek tussen vlak TAC en
lijn TD. |
|
|
c. |
Bereken de hoek tussen vlak TDB en
lijn DM (M is het midden van AB). |
|
|
|
|
|
|
|
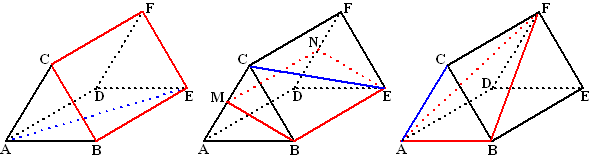
| 3. |
Hieronder staat drie keer een prisma
ABC.DEF waarvan ABC en DEF gelijkzijdige driehoeken met zijde 6
zijn.
AD = 10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a. |
Bereken de hoek tussen vlak CBEF en
lijn AE. |
|
|
b. |
Bereken de hoek tussen vlak BMNE en
lijn CE als M en N middens van de ribben zijn. |
|
| |
c. |
Bereken de hoek tussen vlak ABF en
lijn AC. |
|
| |
|
|
|
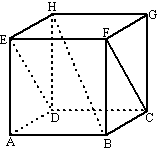
| 4. |
Bereken in kubus
ABCD.EFGH de hoek tussen HB en EFCD |
 |
| |
|
|
|
|
| 5. |
examenvraagstuk VWO Wiskunde B,
2000. |
| |
|
|
|
|
| |
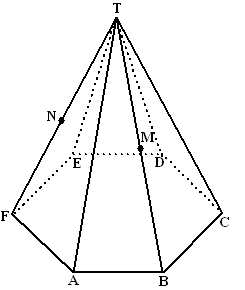
In de figuur
hiernaast is de regelmatige zeszijdige piramide T.ABCDEF getekend.
De middens van de ribben BT en FT zijn achtereenvolgens M en N.
Gegeven is verder dat AB = 6 en dat de afstand van T tot het
grondvlak ABCDEF gelijk is aan 6√3.Bereken de hoek tussen de lijn AM en het
vlak ABCDEF |
 |
| |
|
|
|
|
| |
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|