Nieuwe pagina 1

© h.hofstede (h.hofstede@hogeland.nl)

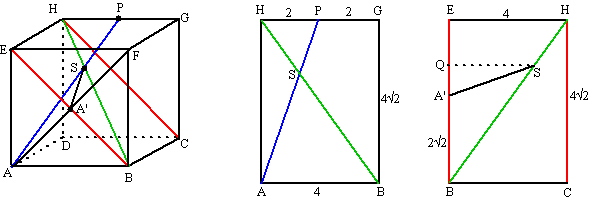
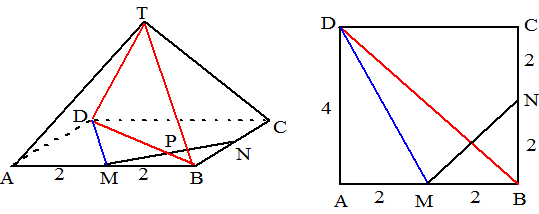
Voor de lengte van de ribben van de kubus heb ik 4 genomen.

Het snijpunt van AP met vlak EBCH is het snijpunt S van AP en HB (AP ligt in hulpvlak AHGB)
De projectie van A op vlak ABCH is het snijpunt A' van EB en AF (immers AF staat loodrecht op EB en op BC dus op heel vlak EBCH).

Het gaat om de hoek ASA' in de figuur hierboven links..

In de middelste figuur zie je dat driehoek HSP de helft van driehoek ASB is, dus SB = 2 • HS
HS = ¹/₃HB dus in de rechterfiguur ligt S op ¹/₃ van HB.
Dan is EQ = ¹/₃EB
EA' = ¹/₂EB dus QA' = ¹/₆EB = ¹/₆ • 4√2 = ²/₃√2
QS = ²/₃BC = ²/₃ • 4 = ⁸/₃
A'S² = (⁸/₃)² + (²/₃√2)² = 8 dus A'S = √8

Omdat A'A = ¹/₂AF = 2√2 geldt in driehoek ASA' dat tanASA' = ^AA'/_A'S = ^2√2/_√8 = 1
Dan is ∠ASA' = 45º

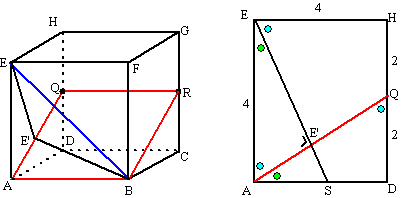
Het snijpunt van EB met vlak EBRQ is uiteraard punt B
Teken lijn EE' loodrecht op AQ
Het gaat om hoek EBE' in de linker figuur hierboven

In de rechter figuur zie je dat de driehoeken EE'A en ADQ en EAS gelijkvormig zijn
ADQ en EAS zijn precies even groot, dus AS = 2
^EE'/_EA = ^AD/_AQ dus ^EE'/₄ = ⁴/_√20 geeft dat EE' = ¹⁶/_√20
^AE'/_AE = ^QD/_AQ dus ^AE'/₄ = ²/_√20 geeft dat AE' = ⁸/_√20

In driehoek ABE' geldt dan E'B² = 4² + (⁸/_√20)² = 19,2 dus E'B = √19,2
in driehoek EBE' geldt dan tanEBE' = ^EE'/_E'B = ⁽¹⁶/√20)/_√19,2 = 0,8165
Dus ∠EBE' = 39,2º

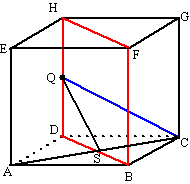
Het snijpunt van CQ met vlak HDBF is uiteraard punt Q.
CS staat loodrecht op vlak HDBF (want bijv. loodrecht op DB en op HD)
Het gaat dus om hoek SQC.

QC² = 4² + 2² = 20 dus QC = √20
CS² = 2² + 2² = 8 dus CS = √8

In driehoek QSC is dan sinQSC = ^CS/_QC = ^√8/_√20 = 0,6325
Dan is ∠QSC = 39,2º

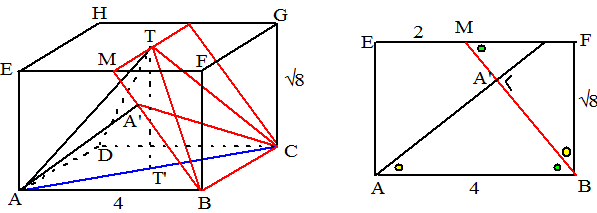
Teken balk ABCD.EFGH om de piramide.
T' is de projectie van T op het grondvlak.
BT' ² = 2² + 2²= 8 en TT'² = BT² - BT´² = 16 - 8 = 8 dus TT' en de hoogte van de balk zijn √8

Teken in het voorvlak van de balk lijn AA' loodrecht op BM, dan staat die lijn ook loodrecht op BC, dus op het hele vlak BTC. A' is de gezochte projectie van A op BTC.
Het gaat om hoek A'CA

In het voorvlak van de balk zijn de driehoeken MFB en BA'A gelijkvormig, en MB² = 2² + 8 = 12 dus MB = √12
^MF/_MB = ^BA'/_BA dus ²/_√12 = ^BA'/₄ en dat geeft BA' = ⁸/_√12
^FB/_MB = ^A'A/_BA dus ^√8/_√12 = ^A'A/₄ en dat geeft A'A = ^4√8/_√12
Dan is A'C = √(BA'² + BC²) = √21¹/₃ (Pythagoras in driehoek BA'C)

In driehoek AA'C geldt tanA'CA = ^AA' /_A'C =^{(4√8/√12)}/√21¹/₃) = 0,7071.
Dan is de gevraagde hoek 35,3˚

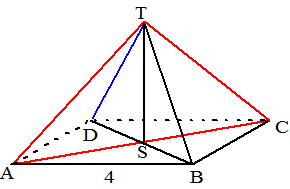
T is het snijpunt van DT met vlak TAC.
S is de projectie van D op vlak TAC.
Het gaat om hoek STD.

SD² = 2²+ 2² = 8 dus SD = √8

sin(STD) = ^SD/_TD = ^√8/₄
dan is ∠STD = 45˚

D is het snijpunt van DM en TDB.
De projectie van M op TDB is punt P, waarbij N het midden van BC is (zie de figuur)
Het gaat om hoek MDP.
In het ondervlak (rechts) geldt: tan(ADM) = ²/₄ dus ∠ADM = 26,56˚
∠ADB = 45˚ dus ∠MDB = 45˚ - 25,56˚ = 18,4˚

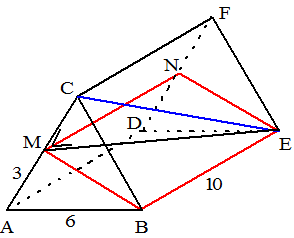
AE snijdt CBEF in punt E.
De projectie van A op CBEF is punt M (midden van BC)
Het gaat om hoek AEM

AM² = AB² - BM² = 36 - 9 = 27 dus AM = √27.

ME² = 3² + 10² = 109 dus ME = √109

tanAEM = ^AM/_ME = ^√27/_√109 = 0,4977

∠AEM = 26,5˚

CE snijdt vlak ABEN in punt E
De projectie van C op vlak ABEN is CM
Het gaat om hoek CEM

CM = 3
ME² = MB² + BE² = (√27)² + 10² = 127

tan(CEM) = ^CM/_ME = ³/_√127 = 0,2662
dan is ∠CEM = 14,9˚

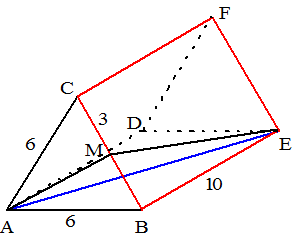
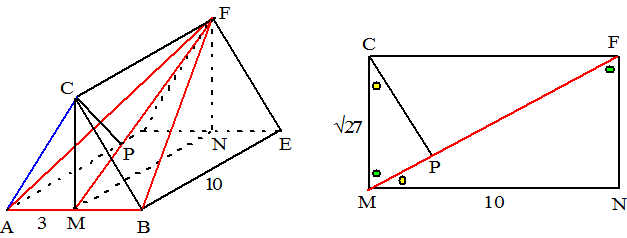
AC snijdt vlak ABF in punt A
De projectie van C op ABF is punt P zodat CP loodrecht op FM staat. (omdat CP in vlak MNFC ligt staat hij ook al loodrecht op AB)
Het gaat om hoek PAC
Zie de rechter tekening.
De driehoeken MPC en FNM zijn gelijkvormig
^CP/_MC = ^MN/_FM dus ^CP/_√27 = ¹⁰/_√127 en dat geeft CP = ^10√27/_√127

sin(PAC) = ^PC/_AC = ^{10√27/√127} / ₆ = 0,7685
Dan is ∠PAC = 50,2˚

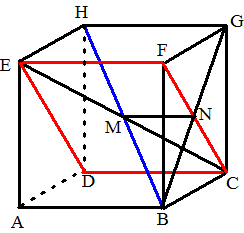
HB snijdt EFCD in het midden M van de kubus.
De projectie van B op vlak EFCD is punt N (midden van BG)
Het gaat om hoek BMN

Stel de ribben van de kubus gelijk aan 4
BN² = 2² + 2² = 8 dus BN = √8
MN = 2

tanBMN = ^BN/_MN= ^√8/₂ = 1,414
∠BMN = 54,7˚

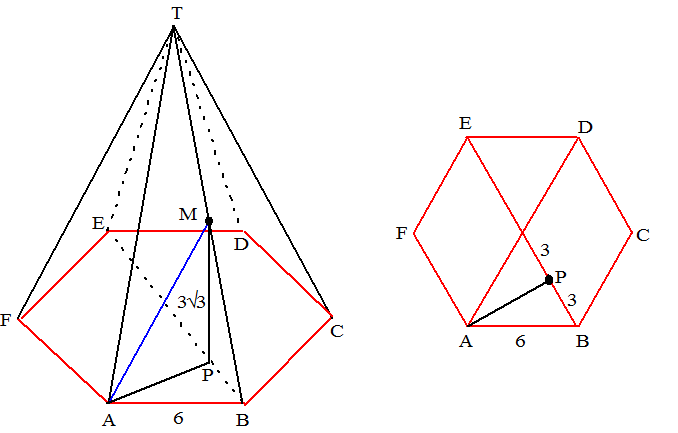
AM snijdt het grondvlak in A
De projectie P van A op het grondvlak ligt op BE.
Zie het bovenaanzicht rechts, met allemaal gelijkzijdige driehoeken met zijden 6.
AP² = 6² - 3² = 36 - 9 = 27 dus AP = √27
Verder is MP de helft van de totale hoogte (M ligt halverwege TB) dus MP = 3√3

tanMAP = ^MP/_AP = ^3√3/_√27 = 1
Dan is ∠MAP = 45˚