|
|||||||
| We kennen nu twee "dingen" in de
ruimte die hoeken met elkaar kunnen maken, en dat zijn lijnen en
vlakken. Er zijn dus drie mogelijkheden voor die hoeken: lijn-lijn,
vlak-vlak en lijn-vlak. Weet je wat? We doen ze gewoon alle drie! 1. De hoek tussen een lijn en een lijn. Dat is de eenvoudigste: de richtingsvector geeft de richting van de lijn aan, dus je neemt gewoon de hoek tussen de beide richtingsvectoren. Voorbeeld. |
|||||||
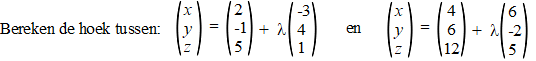 |
|||||||
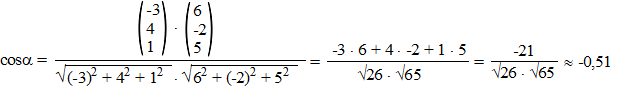 |
|||||||
| Dat geeft
α ≈ 120,72º. Meestal is het gebruikelijk om de niet-stompe hoek te noemen, en die is in dit geval dan 180º - 120,72º = 59,28º (dat kun je ook direct bereiken door van het inproduct de absolute waarde te nemen) |
|||||||
| 2. De hoek tussen een lijn en een vlak. | |||||||
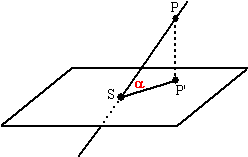
| Het gaat in dit geval om de hoek
tussen die lijn en zijn projectie op dat vlak. (In
deze les staat daar wat
meer over, alleen is het rekenwerk daar wat onhandig). Je zou om die hoek PSP' hiernaast als volgt te werk kunnen gaan: • Bereken het snijpunt van de lijn en het vlak. • Leg een lijn door P met als richtingsvector de normaalvector van het vlak • Snij die lijn met het vlak (dat geeft punt P') • Bereken de hoek tussen de vectoren PS en P'S. |
|
||||||
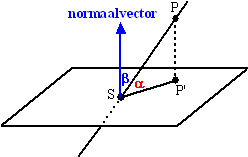
| Daar kom je best uit,
denk ik. Maar toch is dit een nogal onhandige methode. Het kan veel sneller als je de normaalvector van het vlak tekent. Hiernaast zie je dat de hoeken α en β samen 90º zijn. Die hoek β kun je direct uitrekenen: het is de hoek tussen de richtingsvector van de lijn en de normaalvector van het vlak. Dan is α = 90º- β. |
|
||||||
|
|||||||
| Voorbeeld. | |||||||
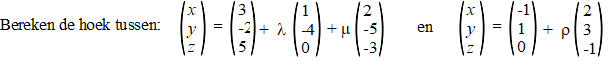 |
|||||||
| Da's mazzel; daar staat al een nul in die richtingsvector van het vlak. Dan is de normaalvector snel te vinden. | |||||||
 |
|||||||
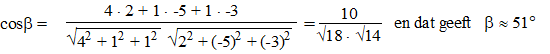 |
|||||||
| De gevraagde hoek is dan ongeveer 90º- 51º = 39º | |||||||
| 3. De hoek tussen een vlak en een vlak. | |||||||
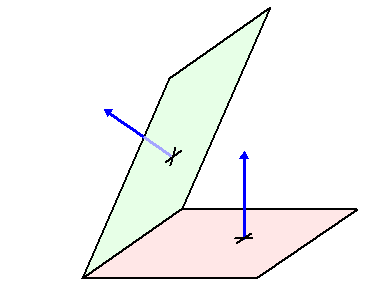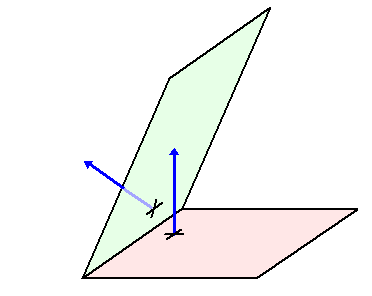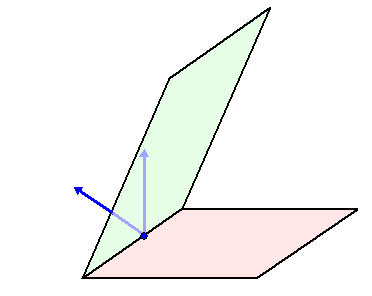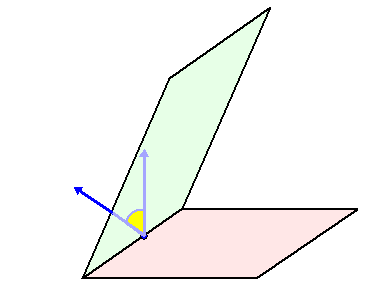
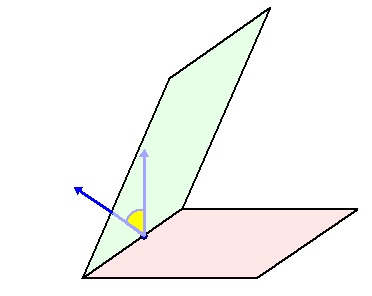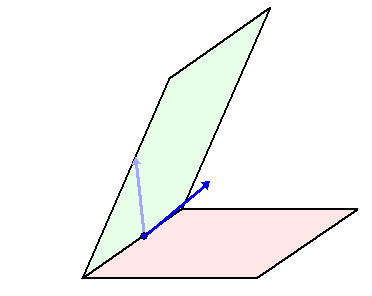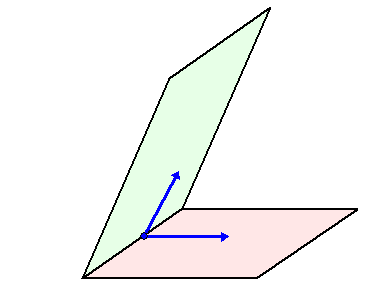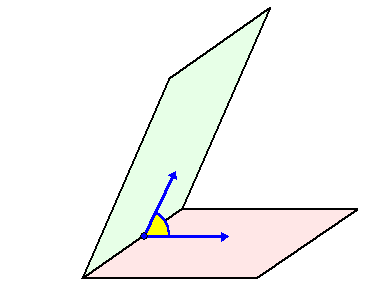
| De hoek tussen twee vlakken is gelijk aan de hoek tussen hun normaalvectoren. In de onderstaande twee plaatjes zie je daar een illustratie van. | |||||||
|
|||||||
| Links worden de
normaalvectoren eerst naar elkaar toegeschoven, en kun je zien dat de
gele hoek de hoek daartussen is. Rechts worden de normaalvectoren samen gedraaid, en kun je zien dat de gele hoek ook de hoek tussen de vlakken is. Die beide blauwe richtingen liggen in het "standvlak". Dat is het vlak dat loodrecht op de snijlijn van beide vlakken staat. |
|||||||
|
|||||||
| Voorbeeld. Ach, deze keer maar eens niet. 't Is eigenlijk te simpel voor woorden.... Meteen maar naar de oefeningen: |
|||||||