| |
|
 |
| |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
| 1. |
Van een dakgoot goot is de breedte van de bodem
40 cm en de lengte van de
opstaande zijwanden 20 cm.
Een dwarsdoorsnede staat in de
figuur hiernaast.
De oppervlakte (O) van zo'n dwarsdoorsnede hangt af van de
hellingshoek
α van de opstaande wanden.
Voor deze oppervlakte O
blijkt te gelden: |
 |
| |
|
|
|
| |
O = 400 ·
sinα · cosα
+ 800 · sinα |
|
| |
|
|
|
| |
a. |
Toon aan dat deze
formule juist is. |
| |
|
|
|
| |
b. |
Bereken algebraïsch
de maximale oppervlakte van zo'n doorsnede. |
| |
|
|
|
| |
|
|
|
| 2. |
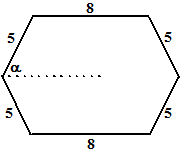
Een zeshoek heeft
vier zijden van 5 cm en twee zijden van 8 cm. Zie de figuur hiernaast.
De oppervlakte van deze zeshoek hangt af van de hoek
α volgens de formule: O(α)
= 50cosαsinα +
80sinα |
 |
| |
|
|
| |
a. |
Toon dat aan |
| |
|
|
| |
b. |
Bereken de maximale oppervlakte van de zeshoek. |
| |
|
|
|
| |
c. |
Bereken
algebraïsch de maximale oppervlakte van de zeshoek. |
| |
|
|
|
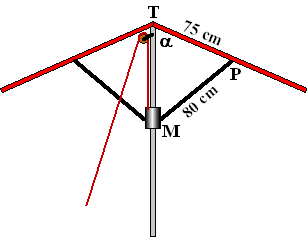
| 3. |
Een parasol open je door aan een touw te
trekken. Het touw loopt via een katrol naar de manchet M. Met het touw
kun je M over de staander omhoog trekken. De uitzetter MP zit
scharnierend vast aan de balein TP.
Hoek MTP noemen we
α.
Bij een geheel gesloten parasol is dus
α =
0° en is de afstand TM = 75 + 80 = 155 cm.
Tijdens het openen neemt a toe en wordt TM kleiner.
De volgende formule blijkt te gelden: |
 |
| |
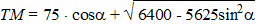 |
| |
|
|
|
| |
a. |
Toon dat aan |
|
| |
|
|
|
| |
b. |
Bepaal voor welke
α
TM het snelst afneemt als functie van
α. |
| |
|
|
|
| |
|
|
|
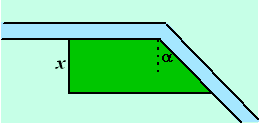
| 4. |
Een boer heeft een stuk weiland waardoor een sloot
loopt die een knik maakt, en waarbij hij een stuk land gaat omheinen met
een omheining van totale lengte L (langs het water hoeft geen
omheining).
Zie de figuur hiernaast.
Voor de oppervlakte van het omheinde land geldt:
O =
xL - x2
- 0,5x2 tanα |
 |
| |
|
|
|
| |
a. |
Toon dat aan. |
|
| |
|
|
|
| |
b. |
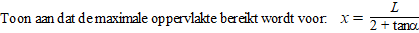 |
| |
|
|
|
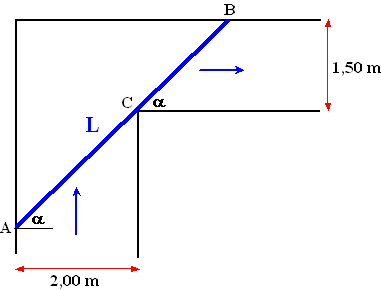
| 5. |
Hiernaast staat het
bovenaanzicht van een gang met een bocht van 90º erin. Het
brede deel is 2 meter breed, het smalle deel 1,50 meter. Iemand
wil een plaat hardboard door de gang de bocht om krijgen. De
plaat is net zo hoog als de gang, dus kan niet omhoog gezet
worden. De dikte van de plaat is te verwaarlozen.
Wat is de langste plaat die de bocht in deze gang kan maken?
(Geef een algebraïsch berekening en je antwoord in cm nauwkeurig) |
|
|
| |
|
|
|
| 6. |
Twee vierkanten
hebben samen oppervlakte 1.
We gaan op zoek naar de rechthoek die we er altijd overheen kunnen leggen
zodat beiden bedekt zijn. De vierkanten mogen elkaar
niet overlappen.
De handigste bedekking is als ze tegen elkaar aan liggen
zoals hiernaast getekend.
Omdat er geldt x2 + y2
= 1 kom je natuurlijk vanzelf op het idee om de lengtes
van de zijden van de vierkanten gelijk te stellen
aan sinα en cosα |
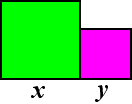
|
|
|
|
| a. |
Laat zien dat de
oppervlakte van de rechthoek dan wordt gegeven door
A = cos2α +
0,5sin2α |
| |
|
| b. |
Bereken
algebraïsch de
maximale oppervlakte van de rechthoek die beiden bedekt. |
| |
|
|
| |
|
|
|
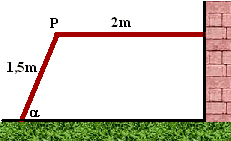
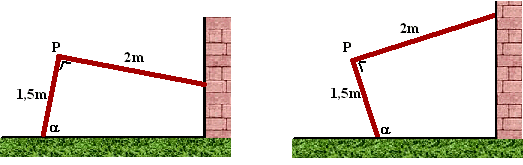
| 7. |
Twee meisjes gaan een hut
maken met twee platen hout die scharnierend in punt P aan elkaar
zijn vastgemaakt. Ze doen dat zoals in de tekening hiernaast. De
platen zijn 2 meter en 1,5 meter lang.
Aan de muur en op de grond maken ze de platen vast en krijgen zo
de overkapping hiernaast. De bovenkant is horizontaal.
De hoek van de plaat met de bodem is
α.
Voor de oppervlakte van het zijaanzicht hiernaast geldt dan: |
|
| |
|
|
|
| |
|
| O = 3sinα + 1,125sinαcosα |
|
|
| |
|
|
| |
a. |
Toon aan dat deze formule juist is |
| |
|
|
| |
b. |
Bereken algebraïsch de maximale oppervlakte. |
| |
|
|
| |
c. |
Bereken hoeveel procent méér
oppervlakte de meisjes kunnen krijgen door de plaat van 1,5m als
bovenkant te gebruiken. |
| |
|
|
|
| |
Als de platen niet scharnierend maar
vast onder een hoek van 90º aan elkaar zitten dan kunnen ze
beide platen nog steeds onder een hoek
α neerzetten. Het dak is
dan niet meer horizontaal.: |
| |
|
|
|
| |
|
| |
|
|
|
| |
d. |
Bereken welke manier de grootste
oppervlakte geeft. |
| |
|
|
|
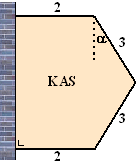
| 8. |
Een tuinder gaat tegen een
muur een kas bouwen. Hij heeft 4 glazen wanden van
2, 3, 3 en 2 meter breed. Die gaat hij tegen de muur
zetten zoals in het bovenaanzicht hiernaast.
De hele figuur gaat symmetrisch worden.
Als de tuinder kiest voor een hoek
α
als in de figuur hiernaast dan geldt voor de
vloeroppervlakte V van de kas:
V =
12cosα + 9sinαcosα |
 |
| |
|
|
|
| |
a. |
Toon aan dat deze formule klopt. |
|
| |
|
|
|
| |
Voor de afgeleide functie geldt V ’ = 9 - 18sin2α
– 12sinα. |
| |
|
|
|
| |
b. |
Toon aan dat deze formule klopt. |
| |
|
|
|
| |
c. |
Als je stelt sinα
= p dan kun je de maximale vloeroppervlakte
algebraïsch berekenen. Voer die berekening uit. |
| |
|
|
|
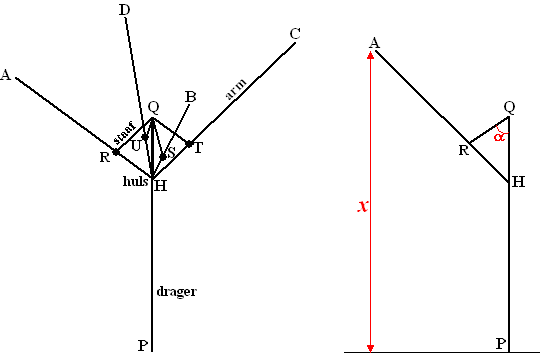
| 9. |
Examenvraagstuk.
Hieronder is een metalen geraamte van een droogmolen getekend.
De waslijnen ontbreken.
Getekend zijn:
• de verticale drager PQ.
• de even lange armen HA, HB, HC en HD
• De even lange staven QR, QS, QT en QU.
De punten R, S , T en U hebben dezelfde afstand tot H. |
| |
|
|
|
| |
|
| |
|
|
|
| |
In H zit een ringvormige huls om de
drager. Deze huls kan schuiven langs de drager en met een
schroefje op elke hoogte worden vastgeklemd. De hoogte van H ten
opzichte van de grond is dus variabel. Alle overige verbindingen
tussen twee onderdelen zijn zo gemaakt dat die onderdelen alleen
maar ten opzichte van elkaar kunnen draaien.
Als de huls langs de draaier wordt geschoven verandert de stand
van de armen. Daardoor verandert de hoogte van de vrije
uiteinden A, B, C en D.
Vat in deze opgave drager, armen en staven op als lijnstukken en
de huls en overige verbindingen als punten.
Afmetingen in cm: PQ = 200, QR = 40, AR = 120 en HR = 60.
α is de hoek in radialen die de
staaf RQ maakt met de drager PQ. De hoogte (in cm) van het vrije
uiteinde A van de arm HA ten opzichte van de grond noemen we x.
Zie de figuren hierboven.
Er zijn twee standen waarbij de molen geheel is dichtgeklapt
(zodat de armen verticaal omhoog staan). |
| |
|
|
|
| |
a. |
Bereken de
bijbehorende waarden van x |
|
| |
|
|
| |
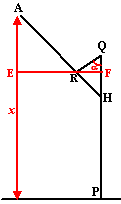
b. |
Bereken x
als
α = 1/6π
Gebruik het feit dat in de figuur hiernaast geldt
dat
x = PQ - QF + AE |
| |
|
|
| |
De afstand van R
tot PQ kan in
α worden
uitgedrukt en met behulp van die afstand kan het verband
tussen x en a gevonden
worden.
Voor 0 ≤
α ≤
π
geldt de formule: |
| |
|
|
| |
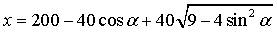
|
|
| |
|
|
|
| |
c. |
Toon de juistheid
van deze formule aan voor 0 ≤
α ≤
1/2π. |
| |
|
|
|
| |
d. |
Toon aan dat de formule hiernaast
klopt. |
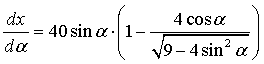 |
| |
|
|
|
| |
Neem aan dat de
huls H zo is vastgeklemd dat
α
= 1/6π.
Iemand schroeft de huls los en schuift hem iets omhoog. |
| |
|
|
|
| |
e. |
Onderzoek met
behulp van dx/dα
of het vrije uiteinde A dan ook omhoog gaat. |
| |
|
|
|
| 10. |
 |
| |
|
| |
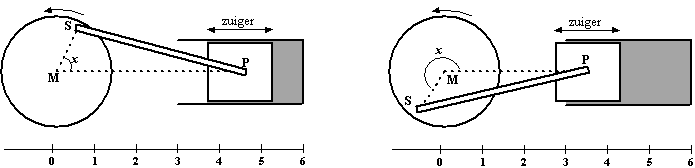
Examenvraagstuk.
Een
zuiger is door middel van een drijfstang verbonden met een draaiende
schijf. Als de schijf draait beweegt de zuiger horizontaal heen en weer.
M is het middelpunt van de schijf. S is het (scharnierende)
verbindingspunt van de drijfstang en de schijf. Bij punt P is de
drijfstang scharnierend met de zuiger verbonden.
MS = 1 en PS = 4. Stel de grootte van hoek PMS is x radialen.
De afstand PM is afhankelijk van x. Stel PM = a(x)
Voor iedere hoekgrootte x geldt a(x) = cosx +
√(16
- sin2 x) |
| |
|
|
|
| |
a. |
Bewijs deze
formule voor 0 ≤ x ≤
1/2π. |
| |
|
|
|
| |
b. |
Het minimum van
de grafiek van a is 3 en het maximum is 5. Hoe kun je dat
beredeneren uit bovenstaande figuur? |
| |
|
|
|
| |
c. |
Bij één
rondgang van de schijf zal PM op twee momenten gelijk zijn aan de lengte
van de drijfstang PS. Hoe groot zijn de hoeken x waarbij dat zich
voordoet? |
| |
|
|
|
| |
De
afstand a kan benaderd worden door b(x) = 4 +
cosx |
| |
|
|
|
| |
d. |
Onderzoek voor
welke x het verschil tussen a en b maximaal is, en
bereken dat maximale verschil in twee decimalen. |
| |
|
|
|
x = 1/2π,
11/2π
verschil 0,13 |
|
| |
|
|
|
| 11. |
examenvraagstuk
HAVO Wiskunde B, 1990
Voor het kweken van plantjes gebruikt
een tuinder een cellenstructuur zoals in de figuur hier onder links
is afgebeeld. Iedere afzonderlijke cel heeft zes zijden van 3 cm.
Door de hele structuur uit te rekken zoals aangegeven in de figuur
rechts, verandert de vorm van iedere cel. Daarbij blijven EF en CB
evenwijdig.
Die verandering kan worden beschreven met behulp van de variabele
hoek DAB. Stel de grootte van hoek DAB is x radialen. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Bereken x in radialen
(in 2 decimalen nauwkeurig) in het geval dat BF = 4 |
| |
|
|
|
| |
Het verband tussen de
oppervlakte van de cel (S) en de hoekgrootte (x) wordt
gegeven door:
S = 18sinx + 18sinxcosx |
| |
|
|
|
| |
b. |
Bewijs de juistheid van deze
formule. |
| |
|
|
|
| |
c. |
Druk dS/dx
uit in cosx |
| |
|
|
|
| |
d. |
Bereken voor welke waarde
van x de oppervlakte van de cel maximaal is. |
| |
|
|
|
| 12. |
examenvraagstuk
HAVO Wiskunde B, 1993. |
| |
|
|
|
| |
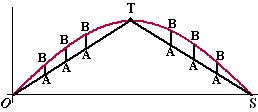
In de figuur hiernaast is de
grafiek getekend van f(x) = sin1/4πx
voor 0 ≤ x
≤ 4.
T is de top van deze grafiek en O en S zijn de randpunten.
We willen deze grafiek gaan benaderen door de lijnstukken OT
en TS. |
 |
| |
|
|
| |
a. |
Stel een vergelijking op
van lijn OT en stel een vergelijking op van lijn TS. |
| |
|
|
|
| |
Het punt A beweegt over de
lijnstukken OT en TS.
Het punt B beweegt over de sinusoïde zo dat lijn stuk AB evenwijdig
aan de y-as blijft. Zie de figuur hiernaast. |
 |
| |
|
|
| |
b. |
Bereken de maximale lengte
van AB in twee decimalen nauwkeurig. |
| |
|
|
|
| 13. |
examenvraagstuk
VWO Wiskunde B, 2005. Een gelijkbenige driehoek met een tophoek van
30º (1/6π
radialen) en twee zijden van lengte 1 wordt op een rechthoekig blaadje
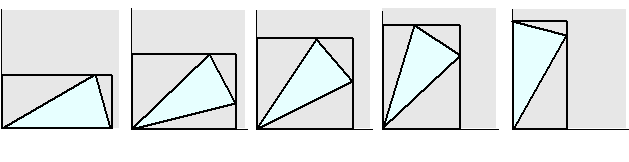
papier gelegd met de top in een hoekpunt van het papier. Vervolgens wordt door elk ander hoekpunt van de driehoek een
lijn getrokken evenwijdig aan een rand van het blaadje. Door de getekende
lijnen en de randen van het blaadje papier wordt zo een rechthoek gevormd. |
| |
|
|
|
| |
 |
| |
In de figuur hierboven is voor
vijf verschillende posities van de driehoek de bijbehorende rechthoek
getekend. |
| |
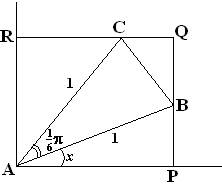
In de figuur hiernaast zijn voor een
willekeurige situatie letters bij de hoekpunten gezet.
Om driehoek ABC met tophoek A is rechthoek APQR gevormd.
Bij elke stand van driehoek ABC hoort een hoek PAB. Noem de
grootte van deze hoek x radialen.
Dus ∠PAB = x met 0 ≤
x ≤ 1/3π.
Verder is AB = AC = 1 en ∠BAC =
1/6π |
 |
| |
|
|
| |
a. |
Bereken voor welke waarde van x rechthoek APQR een
vierkant is. |
| |
|
|
| |
De oppervlakte van rechthoek APQR is een
functie van x en wordt aangegeven met O(x)
Er geldt: O(x) = cosx • cos(1/3π
- x) |
| |
|
|
|
| |
b. |
Toon dit aan |
|
| |
|
|
|
| |
c. |
Bereken de exacte waarden die O(x) kan aannemen. |
| |
|
|
|
| |
|
|
|
| 14. |
Examenvraagstuk
VWO Wiskunde B, 2008. |
|
| |
|
|
|
| |
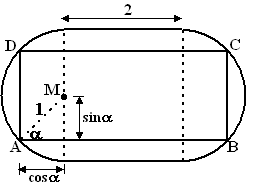
Het ovaal
in de figuur hiernaast bestaat uit een vierkant van 2 bij 2 met aan
weerszijden een halve cirkel met straal 1. M
is het middelpunt van een van de halve cirkels.
n het ovaal wordt een rechthoek ABCD getekend met de
hoekpunten op de halve cirkels en met de zijden
evenwijdig aan de zijden van het vierkant. ∠MAB
= α rad (0 < α < 1/2π).
Hierin is de rechthoekige driehoek AMS te
zien met rechthoekszijden sinα en cosα
.De
oppervlakte O van rechthoek ABCD kan
uitgedrukt worden in α. Er geldt: O = 2sin 2α + 4sinα. |
 |
| |
|
|
|
| |
a. |
Toon aan dat
deze formule juist is. |
| |
|
|
|
| |
Er geldt: dO/dα
= 8 • cos 11/2α
• cos 1/2α. |
| |
|
|
|
| |
b. |
Toon aan dat de formule voor dO/dα
juist is. |
| |
|
|
|
| |
c. |
Bereken
langs algebraïsche weg de maximale oppervlakte van rechthoek ABCD. |
| |
|
|
|
| |
|
|
|
| 15. |
Examenvraagstuk
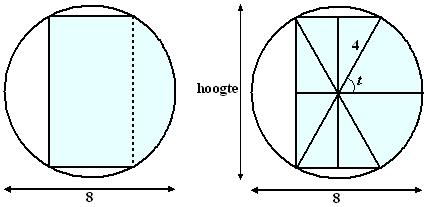
VWO Wiskunde B, 2009. Binnen een cirkel met straal 4 bekijken we gebieden
die bestaan uit een rechthoek (met de hoekpunten op de cirkel), aan de
rechterkant aangevuld met een cirkelsegment. Zo’n gebied heeft dan de
vorm van een rechthoek met een buik. Zie de volgende figuur. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In de rechterfiguur is het gebied verdeeld in twee
cirkelsectoren, beide met middelpuntshoek t radialen, en
zes gelijke rechthoekige driehoeken. Deze driehoeken hebben ook een hoek
met grootte t radialen.
De oppervlakte O van het gebied is een functie van t, met 0
< t < 1/2π
.
Er geldt: O(t) = 16t + 24 • sin2t . |
| |
|
|
|
| |
a. |
Toon de juistheid van deze formule aan. |
|
| |
|
|
|
| |
b. |
Bereken de exacte waarde van O als de hoogte van het
gebied 4 is. |
| |
|
|
|
| |
c. |
Bereken bij welke
hoogte de oppervlakte maximaal is. |
| |
|
|
|
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|