 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
Constructies, hoeken en afstanden. |
| |
|
|
|
| 1. |
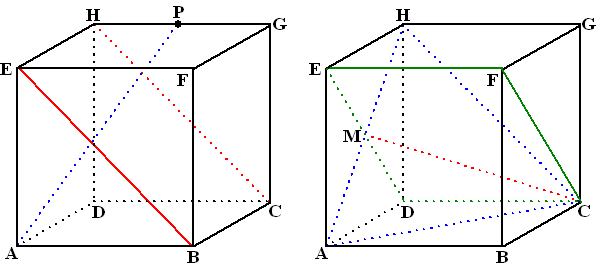
Hieronder
staan twee kubussen ABCD.EFGH.
Links is lijn AP getekend, met P het midden van HG
Rechts zijn de vlakken ACH en EDCF met hun snijlijn CM getekend |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Bereken de hoek tussen lijn AP en
vlak EHBC |
| |
|
|
|
| |
b. |
Bereken de
hoek tussen de vlakken ACH en EDCF |
| |
|
|
|
| |
c. |
Bereken de
afstand van M tot FD als de ribben van de kubus gelijk zijn aan 4. |
| |
|
|
|
| |
|
|
|
| 2. |
Examenvraagstuk
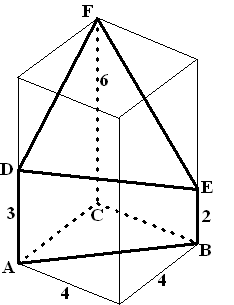
HAVO 1990 Het
lichaam ABC.DEF past in een balk van 4 bij 4 bij 6 dm. D ligt op hoogte
3 dm en E op hoogte 2 dm. Zie de figuur hiernaast. |
 |
| |
|
|
| |
a. |
Bereken de inhoud
van ABC.DEF |
| |
|
|
| |
b. |
Teken een uitslag
van ABC.DEF |
| |
|
|
| |
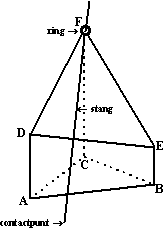
In
punt F bevindt zich een draaibare ring. Door deze ring wordt een metalen
stang geschoven. Deze stang rust op ribbe DE en wordt doorgeschoven
totdat hij de grond raakt (zie onderste figuur) Bij
verschillende standen van de stang horen verschillende contactpunten van
de stang met de grond. |
| |
|
|
|
| |
c. |
Teken de figuur
die gevormd wordt door alle mogelijke contactpunten. |
 |
| |
|
|
| |
d. |
P is het
contactpunt dat het dichtst bij F ligt. Onderzoek of een stang met
lengte 75 cm lang genoeg is om F met P te verbinden. |
| |
|
|
|
| |
|
|
|
| 3. |
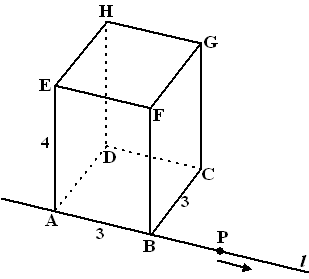
Examenvraagstuk. ABCD.EFGH is een
balk met een vierkant grondvlak (3 bij 3 cm) en een hoogte van 4 cm.
Door de hoekpunten A en B is een lijn l getrokken. Het punt P
beweegt met een constante snelheid van 1 cm per seconde over de lijn in
een richting zoals aangegeven in de figuur hiernaast.
Op t = 0 bevindt P zich in hoekpunt B (de tijd t
wordt gemeten in seconden). |
 |
| |
|
|
| |
a. |
Bereken
de hoek die HP maakt met het grondvlak op t = 0. Rond je antwoord
af op een geheel aantal graden. |
| |
|
|
| |
HP
snijdt het zijvlak BCGF in een punt S. Als P over lijn l beweegt,
verandert de positie van S in het zijvlak BCGF. |
| |
|
|
|
| |
b. |
Beredeneer
dat S over lijn BG beweegt. |
|
| |
|
|
|
| |
c. |
Teken
vlak BCGF op ware grootte en teken daarin de baan die S heeft afgelegd
in het tijdsinterval 0 ≤ t ≤
6. Geef een toelichting bij je tekening. |
| |
|
|
|
| |
d. |
De
snelheid waarmee S over BG beweegt is afhankelijk van t. Druk de
snelheid van S uit in t. |
| |
|
|
|
| |
|
|
|
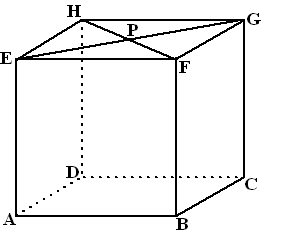
| 4. |
Gegeven
is kubus ABCD.EFGH met ribben van 6 cm.
P is het snijpunt van EG en HF |
 |
| |
|
|
| |
a. |
Bereken de hoek
tussen de lijnen AP en BE |
| |
|
|
| |
b. |
Bereken de hoek
die lijn AP met vlak DBF maakt. |
| |
|
|
| |
c. |
Bereken de hoek
tussen de vlakken ACH en ADH. |
| |
|
|
|
| |
|
|
|
| 5. |
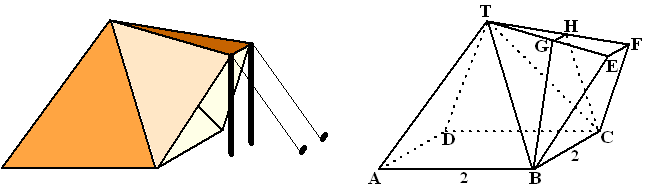 |
| |
|
|
|
| |
Hierboven
links zie je een tekening van een tent. Rechts staat de figuur in zijn
wiskundige vorm, zonder tentdoek, scheerlijnen en stokken nader
uitgewerkt.
Voor de tent is als basisvorm een regelmatige piramide T.ABCD gekozen
met grondvlak 2 m. bij 2 m. en hoogte 1,5 m.
Echter vlak TBC is vervangen door een uitbouw. In deze uitbouw is een
loodrechte wand BGHC gemaakt. Het overblijvende deel (BCGHEF) vormt een
soort overkapping. |
| |
|
|
|
| |
a. |
Bereken in graden
nauwkeurig de grootte van de hoek tussen de vlakken TAD en ABCD. |
| |
|
|
|
| |
EF
ligt 0,8 meter boven de grond en is 0,5 meter lang.
De afstand van EF tot BCGH is 0,5 meter. |
| |
|
|
|
| |
b. |
Bereken de hoek
die EB met het grondvlak maakt. |
| |
|
|
|
| |
c. |
Teken de drie
aanzichten van deze tent met schaal 1 : 50. Geef daarin vlak BCGH met
kleur aan. |
| |
|
|
|
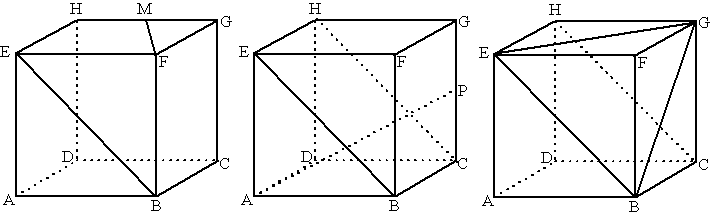
| 6. |
Hieronder staan drie kubussen, elk met ribben 4.
De punten M en P zijn middens van de ribben waarop ze liggen. |
| |
|
|
|
 |
| |
|
|
|
| |
a. |
Bereken
de hoek tussen de lijnen EB en MF |
| |
|
|
|
| |
b. |
Bereken de hoek tussen lijn AP en vlak EBCH |
| |
|
|
|
| |
c. |
Bereken
de hoek tussen de vlakken EBG en EBCH |
| |
|
|
|
| |
|
|
|
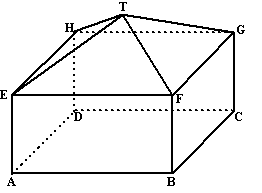
| 7. |
In
een blokkendoos zit het huis hiernaast. Het bestaat uit een balk met een
regelmatige piramide erop.
De afmetingen zijn:
AB = BC = 8, TF = 6,
BF = 4. |
 |
| |
|
|
| |
a. |
Bereken de
afstand van punt T tot het grondvlak. |
| |
|
|
| |
b. |
Het
valt me op dat de vlakken TFG
en EBCH evenwijdig lijken te
lopen.
Bewijs dat dat inderdaad zo is, en bereken de afstand tussen deze beide
vlakken in drie decimalen nauwkeurig. |
| |
|
|
|
| |
c. |
Bereken
de afstand van punt B tot
lijn TG in twee decimalen. |
| |
|
|
|
| |
d. |
Ik
zet een zaag op de middens van TF
en TG en zaag het blok loodrecht naar beneden door. Bereken
de inhoud van het deel rechts van de zaagsnede. |
| |
|
|
|
| |
|
|
|
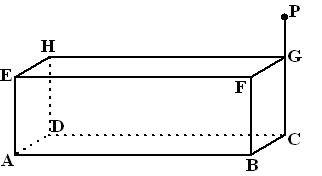
| 8. |
Gegeven is de balk ABCD.EFGH
met AB = 12 en
AE = AD = 4.
P ligt op het verlengde van GC zodat PG = 2.
Lijn AP snijdt het bovenvlak van de balk in punt Q. |
 |
| |
|
|
| |
a. |
Teken punt Q. |
| |
|
|
| |
b. |
Bereken de lengte van AQ |
| |
|
|
|
| |
Vanaf punt P wordt een touw
strak gespannen in één rechte lijn via punt R op ribbe EF naar een
punt S op het verlengde van ribbe DA. |
| |
|
|
|
| |
c. |
Teken de aanzichten van de
balk met het touw. |
| |
|
|
|
| |
d. |
Construeer punt R in de
ruimtelijke figuur |
| |
|
|
|
| |
e. |
Bereken de lengte van DR. |
| |
|
|
|
| |
|
|
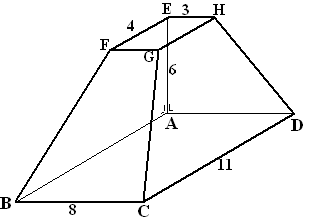
| 9. |
Hiernaast
staat een ruimtelijke figuur ABCD.EFGH. Het grondvlak is een rechthoek
van 8 bij 11, het bovenvlak een rechthoek van 3 bij 4.
Grondvlak en bovenvlak zijn evenwijdig.
Punt E ligt recht boven A.
AE heeft lengte 6. |
 |
| |
|
|
| |
a. |
Teken een uitslag van deze figuur
met schaal 1 : 2. |
| |
|
|
| |
b. |
Teken de drie
aanzichten van deze figuur. |
| |
|
|
|
| |
c. |
Teken
in het bovenaanzicht de hoogtelijnen op hoogte 2 en 4. |
| |
|
|
|
| |
d. |
Bereken
de lengte van FD. |
| |
|
|
|
| |
e. |
Teken
vlak ACGE, en bereken daarmee de hoek die AG en EC met elkaar
maken. |
| |
|
|
|
| |
f. |
Is
deze figuur een afgeknotte piramide?
Leg uit! |
| |
|
|
|
| |
|
|
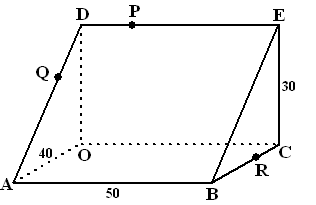
| 10. |
Gegeven
is een prisma AOD.BCE met
AD = AB = 50 en OA = 40 en OD = 30.
P is een punt van DE zodat DP = 15. Q is een punt van AD en R is een
punt van BC zodat RC = 10. |
 |
| |
|
|
| |
a. |
Teken de doorsnede van vlak PQR met het prisma. |
| |
|
|
| |
Het
prisma wordt doorsneden door een vlak dat door P en R gaat en dat
loodrecht op het grondvlak OABC staat. |
| |
|
|
|
| |
b. |
Teken de drie
aanzichten van het prisma met dit vlak erin. |
| |
|
|
|
| |
M is
het midden van BD. We bekijken de route van C naar M over de
grensvlakken van het prisma. Dat kan via een punt S op DE. |
| |
|
|
|
| |
c. |
Hoe
groot moet ES zijn opdat de route van C naar M via S minimale lengte
heeft? |
| |
|
|
|
| |
|
|
|
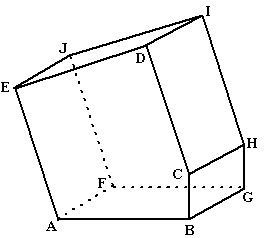
| 11. |
Een
architect heeft het huis ontworpen dat hiernaast in parallelprojectie
staat getekend. Zij maakt er een schaalmodel van. Daarin is ABGF een
vierkant met zijde 6, BC =
3, en ACDE is ook een vierkant. Hoek ABC is 90˚.
De volgende vragen gaan over dit schaalmodel. |
 |
| |
|
|
| |
a. |
Is dit huis een
prisma? Leg uit! |
| |
|
|
| |
b. |
Bereken de
inhoud. |
| |
|
|
| |
c. |
Teken een voor-
zij- en bovenaanzicht. |
| |
|
|
|
| |
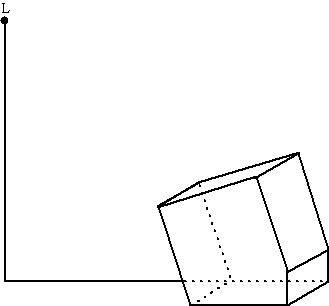
d. |
Op
lijn FG staat een lantaarnpaal. Teken in de figuur hieronder de schaduw
van dit schaalmodel ten gevolge van lichtbron L. Geef een duidelijke
toelichting. |
| |
|
|
|
| |
|
 |
| |
|
|
|
| |
e. |
Er
moet in het huis een vloer komen voor een eerste verdieping. Die vloer
komt op hoogte h boven het grondvlak, en hij ligt horizontaal. De
architect meet voor verschillende waarden van h de oppervlakte (O) van
deze vloer. Schets de grafiek van O(h). |
| |
|
|
|
| 12. |
Examenvraagstuk
HAVO 1990.
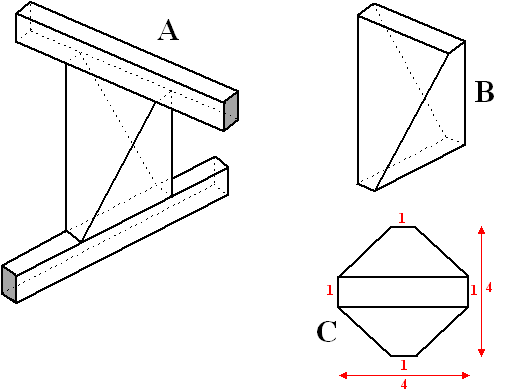
In
een betonconstructie kruisen twee horizontale balken elkaar loodrecht
(zie figuur A). De afstand tussen de balken is 6 meter. De balken zijn
verbonden door een zuil met rechthoekig boven- en ondervlak (zie figuur
B). De middelpunten van de rechthoeken liggen recht boven elkaar. Beide
rechthoeken zijn 1 bij 4 meter. In figuur C zie je een bovenaanzicht van
de zuil. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
De
vier opstaande vlakken maken een even grote hoek met het horizontale
vlak. |
| |
|
|
|
| |
a. |
Bereken de
grootte van die hoek in graden nauwkeurig. |
| |
|
|
|
| |
b. |
Er wordt een
kartonnen model van de zuil gemaakt op schaal 1 : 100. Teken een
bouwplaat van dit model. De bouwplaat mag niet uit losse stukken bestaan
en de plakrandjes hoeven niet te worden getekend. |
| |
|
| |
Rondom
de zuil wordt, op halve hoogte en horizontaal, een lint strak gespannen. |
| |
|
|
|
| |
c. |
Bereken hoe lang
dat lint is. |
| |
|
|
|
| |
d. |
Is het mogelijk
om het lint langs de zuil omhoog (of omlaag) te schuiven zó, dat het
lint horizontaal en strak gespannen blijft? Licht je antwoord toe. |
| |
|
|
|
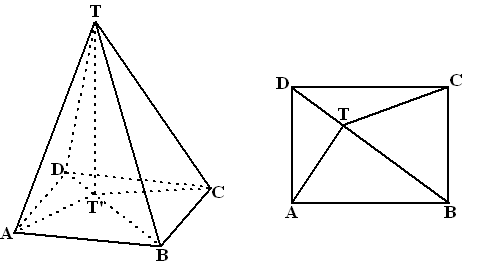
| 13. |
Van
piramide T.ABCD ligt de top T op hoogte 12 boven het grondvlak ABCD. Het
grondvlak is een rechthoek waarin AB = 12 en BC = 9. T' is de loodrechte
projectie van T op het grondvlak. T' ligt zo op lijnstuk BD dat BT' =
2DT'.
Zie de piramide hieronder. Rechts is het bovenaanzicht getekend. |
| |
|
|
|
| |
|
 |
| |
|
|
|
| |
a. |
Bereken
de hoek, tussen de vlakken TAD en ABCD in graden nauwkeurig. |
| |
|
|
|
| |
b. |
Bereken
de lengte van de ribbe AT. |
| |
|
|
|
| |
c. |
Het
vlak door AT loodrecht op het grondvlak verdeelt de piramide in twee
delen. Hoe verhouden zich de inhouden van die twee delen? Licht je
antwoord toe. |
| |
|
|
|
| |
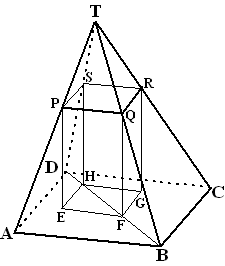
Een
vlak V dat evenwijdig is aan het grondvlak ABCD ligt op afstand x
onder de top (0 < x < 12)
V snijdt de piramide volgens een rechthoek PQRS. PQRS is het bovenvlak
van een balk EFGH.PQRS waarbij EFGH in het grondvlak van de piramide
ligt. Zie de figuur hiernaast. |
 |
| |
|
|
| |
d. |
In de figuur
hiernaast is de situatie getekend voor x = 4. Bereken in deze
situatie de inhoud van de balk. |
| |
|
|
| |
e. |
Onderzoek
wat de maximale inhoud van de balk is als V in hoogte varieert. |
| |
|
|
|
| |
|
|
|
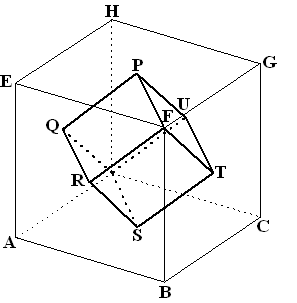
| 14. |
Examenvraagstuk.
In de
kubus ABCD.EFGH met ribbenlengte 6 bevindt zich een ruimtelijk lichaam
L. Van de acht hoekpunten van L zijn er twee tevens hoekpunten van de
kubus, de punten D en F. De overige zes punten van L zijn de middens van
de zijvlakken van de kubus; P, Q, R, S, T en U zijn achtereenvolgens de
middens van de vierkanten EFGH, ADHE, ABFE, ABCD, BCGF en CDHG.
|
 |
| |
|
|
| |
a. |
Toon aan dat alle
ribben van L even lang zijn. |
| |
|
|
| |
b. |
Teken het
aanzicht in de richting van lijn AC van de kubus met daarin het lichaam
L. |
| |
|
|
| |
c. |
Teken vierhoek
RSTF op ware grootte. |
| |
|
|
| |
d. |
Onderzoek of
lichaam L een kubus is. |
| |
|
|
|
| |
Lichaamsdiagonaal
BH staat loodrecht op de vlakken ACF en DEG (dit hoeft niet aangetoond
te worden) |
| |
|
|
|
| |
e. |
Toon
aan dat de afstand van vlak FRST tot vlak PQDU gelijk is aan 2√3 |
| |
|
|
|
| |
f. |
Bereken
zonder af te ronden de inhoud van lichaam L. |
| |
|
|
|
| |
|
|
|
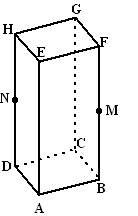
| 15. |
Examenvraagstuk
Van
de balk ABCD.EFGH hiernaast is gegeven:
AB = BC = 4 en AE = 8. M
en N zijn achtereenvolgens de middens van de ribben BF en DH. |
 |
| |
|
|
| |
a. |
Bereken de inhoud
van het viervlak ACFH. |
| |
|
|
| |
b. |
Teken de
doorsnede van vlak AMN met het viervlak ACFH. |
| |
|
|
| |
c. |
Bereken de
afstand tussen de lijnen AM en GN. |
| |
|
|
|
| |
|
|
|
| |
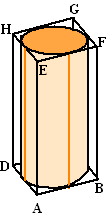
Neem
nu aan dat ABCD.EFGH de binnenkant is van een doos waar een massieve
cilinder precies in past. Een dunne draad komt bij A de doos binnen,
loopt in de doos achter de cilinder om en komt er bij E weer uit. Die
draad wordt zo strak mogelijk aangetrokken. De dikte van de draad mag
worden verwaarloosd. We nemen verder aan dat de draad vrij langs de
cilinder kan glijden, ook op plaatsen waar de cilinder de binnenkant van
de doos raakt. |
 |
| |
|
|
| |
d. |
Teken het
bovenaanzicht van het gedeelte van de draad dat binnen de doos zit en
bereken in één decimaal nauwkeurig de lengte van dit deel van de
draad. Licht je werkwijze toe. |
| |
|
|
|
| |
|
|
|
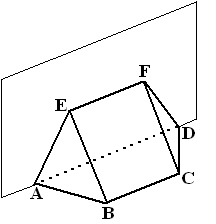
| 16. |
Aan
een muur is een uitbouw ABCD.EF gemaakt (zie tekening). Er geldt
EF = BC = 4 en AD = 10. Vlak ADEF staat loodrecht op het grondvlak ABCD,
en lijnstuk EF bevindt zich op hoogte 4 boven het grondvlak. Ook de
afstand tussen BC en AD is 4.
De uitbouw is symmetrisch. |
 |
| |
|
|
| |
a. |
Bereken de hoek
die de lijnen EB en DF met elkaar maken. |
| |
|
|
| |
b. |
Bereken de hoek
die de vlakken ABE en BCFE met elkaar maken. |
| |
|
|
|
| |
c. |
Bereken de inhoud
van deze uitbouw. |
| |
|
|
|
| |
d. |
Bereken de
afstand van punt A tot vlak EBCF in twee decimalen nauwkeurig. |
| |
|
|
|
| |
|
|
|
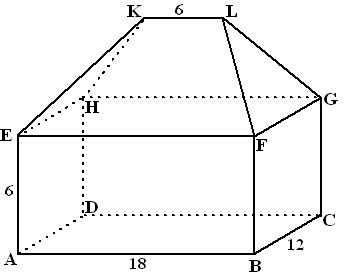
| 17. |
De
figuur hiernaast stelt een huis voor met een zogenaamd
"schilddak". De nok KL bevindt zich 15 meter boven het
grondvlak ABCD.
Verder is AB = 18 m, BC = 12 m, AE = KL = 6 m |
 |
| |
|
|
| |
a. |
Bereken de inhoud
van het huis |
| |
|
|
| |
b. |
In het huis wordt
een horizontale vloer op hoogte h = 9 gelegd. Bereken de
oppervlakte van die vloer. |
| |
|
|
| |
c. |
Bereken de hoek
die lijn LF met vlak EFGH maakt. |
| |
|
|
|
| |
d. |
Bereken de
kortste afstand van punt E tot lijn LF in twee decimalen nauwkeurig. |
| |
|
|
|
| |
e. |
P is een punt van
AB zodat PK = √265. Bereken de afstand AP. |
| |
|
|
|
| |
|
|
|
| 18. |
Gegeven is kubus
ABCD.EFGH met ribben 4.
M is het midden van EH, P is een punt op BC zodat PB = 1. |
| |
|
|
|
| |
a. |
De coördinaten van P
zijn (1, 2, -4). Teken in dat geval de kubus met de oorsprong van
het assenstelsel dat daarbij hoort. |
| |
|
|
|
| |
b. |
Bereken de lengte van
MP |
| |
|
|
|
| |
c. |
Bereken hoek MPG in
twee decimalen nauwkeurig. |
| |
|
|
|
| |
d. |
De kubus wordt
doorgezaagd via vlak ACH. Het deel met punt F gaat eraf.
Teken een voor- zij- en bovenaanzicht van het overgebleven deel. |
| |
|
|
|
| |
e. |
Daarna wordt dit
overgebleven deel nóg eens doorgezaagd, nu langs het vlak dat
oorspronkelijk vlak GCM was. Het deel met punt A gaat eraf.
Maak een ruimtelijke tekening van het overgebleven deel. |
| |
|
|
|
| 19. |
examenvraagstuk
HAVO Wiskunde B, 1989. |
| |
|
|
|
| |
 |
| |
|
|
|
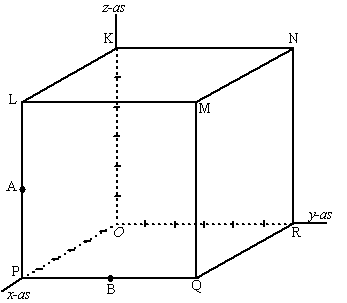
| |
In een Oxyz-assenstelsel ligt de
kubus OPQR.KLMN met ribbe 6.
Hierboven is die kubus in scheve projectie getekend.
Het vlak U gaat door K, R, het midden A van LP en het midden B van
PQ. |
| |
|
|
|
| |
a. |
Bereken de oppervlakte van
vierhoek ABRK. |
| |
|
|
|
| |
Het vlak U wordt in de
richting van de positieve z-as 1 eenheid omhooggeschoven. Zo
ontstaat vlak V. |
| |
|
|
|
| |
b. |
Teken de
doorsnijdingsfiguur van V met de kubus. |
| |
|
|
|
| |
Het diagonaalvlak OPMN is
een rechthoek. Het vlak U snijdt dit diagonaalvlak volgens een lijn
l. |
| |
|
|
|
| |
c. |
Teken de lijn l in
de rechthoek hiernaast. |
 |
| |
|
|
| |
Het vlak U
draait om de lijn KR.
Het snijpunt A van U met LP verandert daardoor van plaats.
Neem aan dat het punt A juist alle posities op de ribbe LP bereikt. |
| |
|
|
| |
d. |
Arceer in de rechthoek
hiernaast het gebied dat bestreken wordt door de snijlijn l
van U met het diagonaalvlak OPMN. |
| |
|
|
|
| 20. |
examenvraagstuk
HAVO Wiskunde B, 2006. |
| |
|
|
|
| |
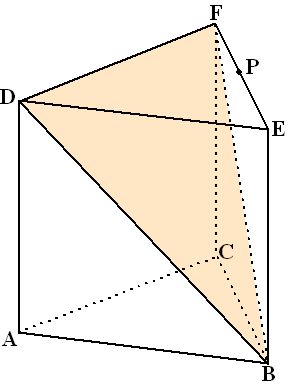
In de figuur hiernaast is het
prisma ABC.DEF getekend. De ribben AD, BE en CF staan loodrecht op de
vlakken ABC en DEF.
De driehoeken ABC en DEF zijn gelijkzijdig met zijden van 6 cm.
Ook de opstaande ribben van het prisma hebben een lengte van 6 cm.
Het vlak BDF verdeelt het prisma in twee piramides (zie figuur). |
 |
| |
|
|
| |
a. |
Bereken de inhoud van de piramide B.ACFD.
Geef je antwoord in cm3 nauwkeurig. |
| |
|
|
| |
P is het midden van ribbe EF.
Lijn AP snijdt vlak BDF in punt S. |
| |
|
|
| |
b. |
Teken het punt S. Licht je werkwijze toe. |
| |
|
|
| |
c. |
Bereken de hoek die lijn BD met vlak ACFD
maakt. Geef je antwoord in gehele graden. |
| |
|
|
|
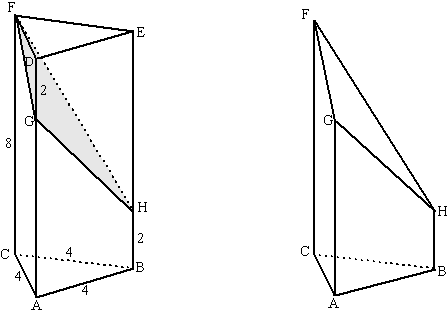
| 21. |
examenvraagstuk
HAVO Wiskunde B, 2014. Gegeven is het prisma ABC.DEF. Het grondvlak ABC is
een gelijkzijdige driehoek met zijde 4.
De hoogte van het prisma is 8. Verder zijn het punt G op ribbe AD en
het punt H op ribbe BE gegeven met DG = BH = 2. Zie de figuur
linksonder.
Lichaam ABC.GHF ontstaat door van het prisma uit de figuur
linksonder een stuk af te snijden met als snijvlak het vlak FGH. Zie
de figuur rechtsonder. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Driehoek FGH is een rechthoekige
driehoek, met de rechte hoek bij G. |
| |
|
|
|
| |
a. |
Toon dit met behulp van exacte berekeningen aan. |
| |
|
|
|
| |
b. |
Hieronder is een begin gemaakt met
een uitslag van ABC.GHF.
Maak de uitslag af. Zet de letters bij de hoekpunten
en licht je werkwijze toe. |
| |
|
|
|
| |
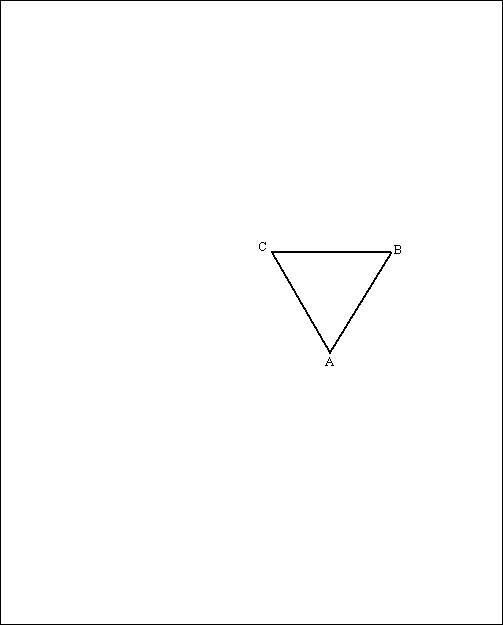 |
| |
|
|
|
| |
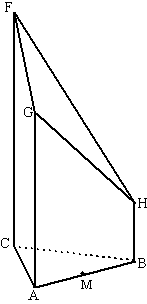
c. |
Punt M is het midden van ribbe AB. Zie
de figuur hiernaast
Teken de doorsnede van ABC.GHF met het
vlak door M evenwijdig aan FGH.
Licht je werkwijze toe. |
 |
| |
|
|
|
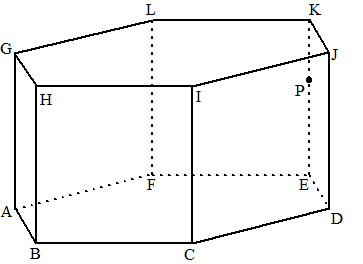
| 22. |
Hiernaast zie je een
regelmatig zeszijdig prisma ABCDEF.GHIJKL getekend waarvan alle ribben 6
zijn.
P is een punt van EK |
 |
| |
|
|
| |
a. |
Teken de doorsnede van vlak ALP
met het prisma. |
| |
|
|
| |
b. |
Bereken de kortste route van H
naar E via de vlakken van het prisma. Geef je antwoord in twee decimalen
nauwkeurig. |
| |
|
|
| |
c. |
Construeer het snijpunt van lijn
BJ met vlak CDK. |
| |
|
|
|
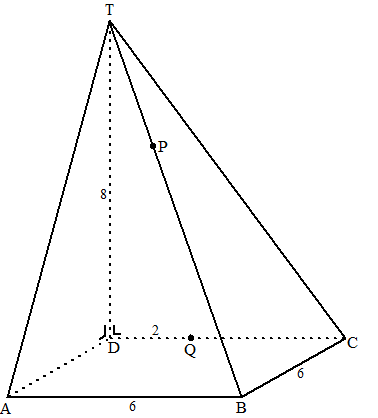
| 23. |
Van piramide T.ABCD
is het grondvlak een vierkant met zijden 6.
D is de loodrechte projectie van T op het grondvlak en DT = 8.
Op BT ligt een punt P zodat BP = 2 • PT.
Op CD ligt een punt Q zodat DQ = 2
Zie de figuur. |
 |
| |
|
|
| |
a. |
Construeer het snijpunt van PQ
met vlak TAC. |
| |
|
|
| |
b. |
Construeer de doorsnede van het
vlak door P en Q dat evenwijdig is aan DT met de piramide. |
| |
|
|
| |
c. |
De doorsnede uit b) verdeelt de
piramide in twee stukken. Bereken de inhoud van het rechtergedeelte. |
| |
|
|
| |
d. |
Bol b
heeft D als middelpunt en straal 5.
Bereken de straal van de snijcirkel van b met
vlak BCT. |
| |
|
|
| |
|
|
|
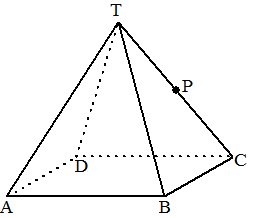
| 24. |
Examenvraagstuk
HAVO, 1969
In een regelmatige
vierzijdige piramide T.ABCD zijn alle ribben even lang.
Het midden van de ribbe CT is het punt P. |
 |
| |
|
|
| |
a. |
Construeer de doorsnede van de piramide met
het vlak dat door A en P gaat en dat evenwijdig aan BT is. |
| |
|
|
| |
b. |
Bereken
∠BPD. |
| |
|
|
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |