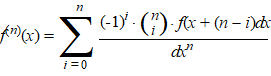gedeeltelijk differentieren


Gedeeltelijk Differentiëren.	© h.hofstede (h.hofstede@hogeland.nl)

Wat is nou weer "Gedeeltelijk Differentiëren" ?
Je differentieert of je doet het niet.

Punt uit.

Of moet je als je ermee bezig bent dan halverwege stoppen of zo??

Niets van dat alles.

Kijk we weten al lang wat de eerste afgeleide van een functie is (gewoon één keer differentiëren)
En we weten ook wat de tweede afgeleide is (twee keer differentiëren)
En de derde afgeleide is uiteraard drie keer differentiëren.

Maar wat zou bijvoorbeeld "een half keer differentiëren" zijn? Of "1,4 keer differentiëren?"

Als we de eerste afgeleide noteren als f⁽¹⁾(x) en de tweede afgeleide als f⁽²⁾(x) enzovoorts, dan is de vraag van vandaag:

Hoe groot is f ^(p)(x) met p een breuk ????

Een eerste poging.

Er is één functie die zich er erg goed voor leent om dit probleem te onderzoeken, en dat is de functie f(x) = e^ax
Kijk maar naar de volgende regelmaat:

f '(x) = ae^ax en f ''(x) = a²e^ax en f⁽³⁾(x) = a³e^ax en .... en...... f⁽ⁿ⁾(x) = aⁿe^ax
Wiskundigen zijn GEK op regelmaat!!!!
Daarom gaan we proberen of dat ook voor breuken kan gelden:

f (x) = e^ax geeft de p^de afgeleide: f^(p)(x) = a^pe^ax

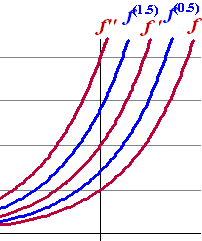
Hiernaast zie je dat dat in grafieken redelijk lijkt te kloppen.
De "gewone" (gehele) afgeleiden zijn rood getekend, en daar precies tussenin liggen de blauwe afgeleiden f^(0,5)(x) en f^(1,5)(x).

Klinkt logisch toch?

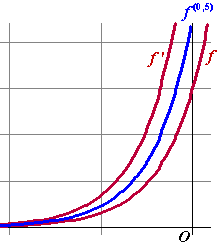
En nu kunnen we ook de gedeeltelijke afgeleide van combinaties van machten van e maken. Zo zal de "halfde afgeleide" van 2e^2x + e^3xgelijk zijn aan:

f^(0,5)(2e^2x + e^3x) = 2√2 • e^2x + √3 • e^3x

Hieronder zie je deze f, f ' en f^0,5 Het lijkt allemaal redelijk te kloppen.

Kennen we zulke combinaties van e-machten?

Jazeker! Met complexe getallen wel!!

Die zijn we immers tegengekomen bij sinx en cosx
Laten we die dan ook maar gedeeltelijk gaan differentiëren, neem bijvoorbeeld f(z) = cosz:

Geeft:

Maar e^0,5^πi = cos¹/₂π + i • sin¹/₂π = i
Dus dan geldt ook: i^p = (e^0,5πi)^p = e^0,5πip en op dezelfde manier (-i)^p = e^-0,5πip

= ¹/₂(cos(¹/₂πp + z) + isin(¹/₂πp + z) + cos(-¹/₂πp - z) + isin(-¹/₂πp - z))

Maar omdat cos(-x) = cosx tellen die cosinussen bij elkaar op, en omdat sin(-x) = -sinx vallen die sinussen weg.
Dat geeft dan uiteindelijk: f^(p) (z) = cos(z + ¹/₂πp)

f(x) = cosx ⇒ f^(p)(x) = cos(x + ¹/₂πp)

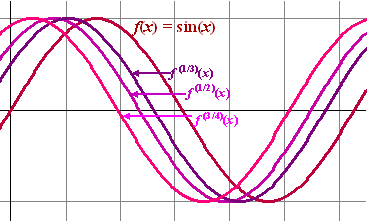
Om cosz gedeeltelijk te differentiëren moet je de grafiek een gedeelte van 0,5π naar links schuiven. Neem p = 1 en je krijgt als afgeleide cos(x + 0,5π) en dat is inderdaad precies gelijk aan -sinx
En als je precies dezelfde berekening voor sinz maakt dan krijg je:

f(x) = sinx ⇒ f^(p)(x) = sin(x + ¹/₂πp)

Andere functies.

Andere functies zijn wat lastiger gedeeltelijk te differentiëren. Er zijn twee mogelijke manieren van aanpak.
Je kunt een functie door middel van Fourieranalyse gaan schrijven als de som van sinussen en cosinussen en die dan als hierboven differentiëren. Dat is niet makkelijk, en heeft bovendien als nadeel dat de Fourier-getransformeerde functie alleen te maken is voor een functie die periodiek is, dus bij een simpele functie als f(x) = x moet je kiezen voor welk stuk van de grafiek je de (gedeeltelijke) afgeleide wilt maken; het kan in het algemeen niet voor de hele grafiek in één keer!

Je kunt het ook met de basisformule voor de afgeleide functie gaan proberen.
Die is:

Deze formule nog een keer toepassen geeft voor de tweede afgeleide (de afgeleide van de afgeleide f ' ):

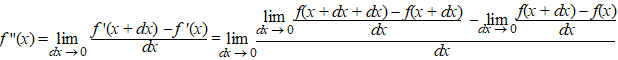Nou, vooruit dan maar: nog een keer differentiëren voor f⁽³⁾(x):

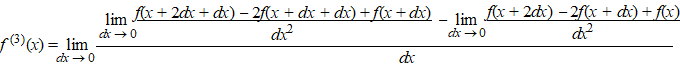Ik hoop dat je de regelmaat ziet.
Daar in de teller staat steeds een dx minder, afwisselend een + en een - teken, en de getallen die verschijnen zijn de binomiaalcoëfficiënten (nCr).
Dat geeft voor f ⁽ⁿ⁾(x):

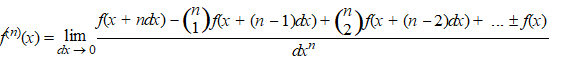Die plussen en minnen kun je handig aangeven als machten van -1, en deze hele formule ziet er natuurlijk wel erg mooi uit als je er een somteken voor gebruikt:

Mooi hé?
Laten we de formule voor de grap even uittesten op de tweede afgeleide van x³Dat geeft voor de teller van f⁽²⁾(x): (x + 2dx)³ - 2(x + dx)³ + x³ = x³ + 6x²dx + 12xdx² + 8dx³ - 2x³ - 6x²dx - 6xdx² - 2dx³ + x³= 6xdx² + 6dx³Delen door dx² en dan dx naar nul laten gaan geeft inderdaad (gelukkig maar) precies als tweede afgeleide f ''(x)= 6x

En nu naar breuken....

Als je nu voor n een breuk neemt en probeert de bovenstaande formule te gebruiken dan kom je twee problemen tegen.
Het eerste probleem is: "Hoe behandel je een somteken met als bovengrens een breuk?" en het tweede probleem is" "Wat zijn de binomiaalcoëfficiënten als er breuken in staan?"

Probleem 1.
Probleem 1 is op te lossen door te kijken waar de n nou eigenlijk vandaan kwam.
In de formule voor de afgeleide gebruikten we de functiewaarden f(x), f(x + dx), f(x + 2dx) , ..., f(x + ndx), en we sommeerden dat van 0 tot en met n.

Probleem 2.
Deze is nogal wat moeilijker op te lossen. Je moet er eerste deze les over de Gamma functie G(x) voor bestuderen.

(rest volgt later...)