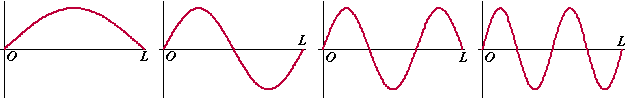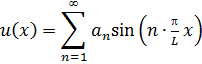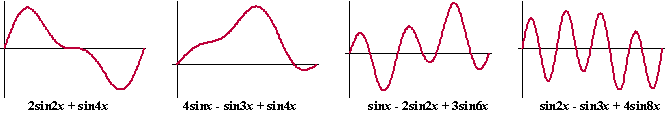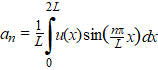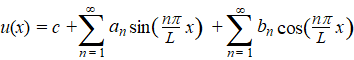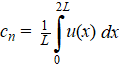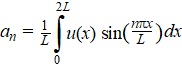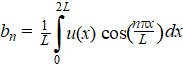Fourier-Analyse.

ฉ h.hofstede (h.hofstede@hogeland.nl)
       
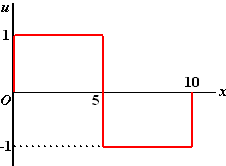
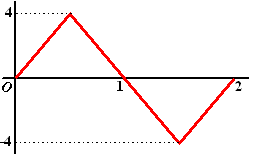
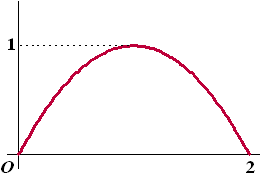
Neem een snaar met lengte L (lopend van x = 0 tot x = L) die aan de uiteinden vastzit, en die we aan het trillen brengen. 
Dan zullen er sinusvormige trillingen ontstaan met als voorwaarde dat de uitwijking u(x) bij x = 0 en x = L gelijk is aan 0.
Deze vormen zijn bijvoorbeeld mogelijk:
       

       
(De amplitudes zijn hier allemaal gelijk getekend maar dat hoeft natuurlijk niet).
De golflengtes (de periodes) in de figuren hierboven zijn achtereenvolgens gelijk aan λ = 2L, λ = L, λ = 2/3L, λ = 1/2L, .....
Zoals je al aan die figuren ziet passen alle golflengtes een geheel aantal keer in 2L.
 
Alle periodes zijn een deler van 2L. 
 

Als je de formule u = asinbx noemt, dan is die a de amplitude, en b is gelijk aan 2π/l.
Dat geeft  b-waarden van achtereenvolgens  π/L,  2π/L,  3π/L,  4π/L, ..... nπ/L 
De grafieken hierboven worden dus gegeven door:
u1(x) = a1sin(π/L• x)  en   u2(x) = a2sin(2π/L• x)  en  u3(x) = a3sin(3π/L• x)  en   u4(x) = a4sin(4π/L• x)  enz.
   

Nou zal de meest algemene vorm die zo'n snaar kan hebben een combinatie zijn van een willekeurig aantal van deze sinusfuncties bij elkaar opgeteld.

Ze kunnen allemaal eventueel verschillende amplitude a hebben, dus je kunt in het algemeen stellen:
       

u(x) = a1sin(π/L• x)  +  a2sin(2π/L• x) + a3sin(3π/L• x) + a4sin(4π/L• x) + .......
       
Wacht... dat kan netter.
Wiskundig kunnen we dit natuurlijk veel eleganter schrijven als:
       

       
Dat geeft oneindig veel mogelijkheden van vormen.  Hier zie je er aan paar:
       

       
Je ziet dat er de vreemdste vormen uit kunnen komen. Het enige dat deze functies gemeenschappelijk hebben is, dat ze zich gaan herhalen. Hierboven is het stuk van x = 0 tot x = L getekend. De stukken van x = L tot x = 2L en van x = 2L tot x = 3L en zo verder zien er precies zo uit. Hierboven is dus steeds ้้n gemeenschappelijke periode (van lengte L) getekend.

Een interessante vraag.
       
De Franse wiskundige Joseph Fourier (ongeveer 1800) vroeg zich af, of je uit zo'n vreemde grafiek (die een combinatie van een heleboel sinussen is) kunt terugvinden uit welke sinussen (met welke periode en welke amplitude) de grafiek is opgebouwd.

Volgens mij zou je raar opkijken als ik nu zou zeggen  "Nou, dat is hem helaas niet gelukt, en daarmee stopt deze les".

Uiteraard is hem dat w้l gelukt, en kun je zijn succesverhaal in de rest van deze les bewonderen.

Zijn probleem was dus: 
Stel ik heb een functie u(x), met u(0) = u(L) = 0
Kan ik die functie dan schrijven als:

u(x) = a1sin(π/L• x) + a2sin(2π/L• x) + a3sin(3π/L• x) + .......   (1)

       
Wat moet ik dan voor a1, a2, a3...  enz kiezen?
       
De geniale inval...
       
Fourier bedacht:  "Als ik an wil weten, dan vermenigvuldig ik alles in vergelijking (1) met sin(nπ/L• x) en neem dan van beide kanten de integraal over ้้n periode".

Dat geeft:
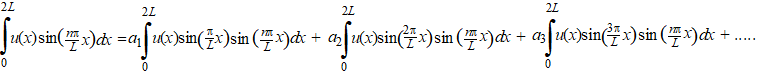Daar aan de rechterkant staan oneindig veel termen.

Maar ze zijn bijna allemaal nul!!!!!!

Waarom?

Dat zit hem in de volgende gonioformule:   sina • sinb = 1/2cos(a - b) - 1/2cos(a + b)
Je kunt hem vrij makkelijk afleiden uit de formules van Simpson die in deze les zijn behandeld. (Gebruik daar de laatste van de vier gegeven formules).

In dit geval geeft dat:    sin(mπ/L • x) • sin(nπ/L • x)  = 1/2cos(πx/L • (m - n))  -  1/2cos(πx/L • (m + n))
Nu staan er aan de rechterkant twee cosinussen.
Maar (m - n)  en (m + n)  zijn gehele getallen.
De periode van  cos(πx/L•(m ฑ n))  is gelijk aan  2L/(m ฑ n) dus dat past een geheel aantal keer in 2L.
Dus de cosinussen passen beiden een geheel aantal keer in 2L.

Dat betekent dat de integraal over een gehele periode ervan nul is. Als je van 0 tot 2L integreert, dan zitten die grafieken even vaak boven de x-as als eronder, dus wordt de totale oppervlakte NUL.

Er is ้้ntje niet nul!

Dat is de term waarin m en n gelijk zijn, dus  sin(nπ/L • x) • sin(nπ/L • x).
Dan wordt 1/2cos(πx/L • (m - n)) - 1/2cos(πx/L • (m + n)) = 1/2 - 1/2cos(2nπx/L)
Dat laatste stuk geeft weer nul (zelfde redenering als hierboven), maar die eerste 1/2 niet.  Die blijft over.
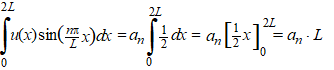Daarmee is an gevonden:

       
Zo kun je ้้n voor ้้n alle an opsporen.

Voorbeeld.
We gaan de eenvoudige blokfunctie u(x) hiernaast benaderen met een serie sinussen. Er is genomen L = 5 zoals je ziet.
Dat geeft achtereenvolgens:

   
 
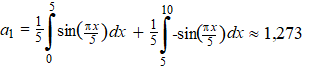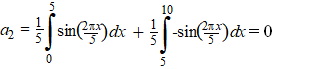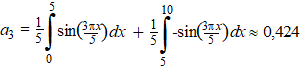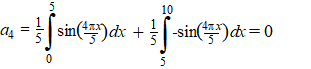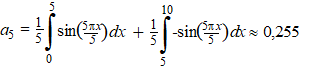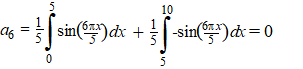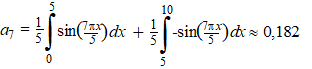enzovoorts.    
     
Kortom, deze blokfunctie is te schrijven als:
 
     
Hieronder zie je hoe dat inderdaad steeds meer op die blokfunctie begint te lijken. Bij elk volgens plaatje is er een term extra van de functie hierboven toegevoegd.
     

     
         
1. Geef van de functie hiernaast een benadering met sinusgrafieken.

         
2. Hiernaast is de parabool  y = 2x - x2  getekend.
Geef een benadering met sinusgrafieken.

         
     
Een uitbreiding.
         
Het hele verhaal hierboven ging er van uit dat u(0) = 0 en u(L) = 0. Ofwel dat de snaar vastzit op de plaatsen 0 en L.
Daarom kregen we als vergelijkingen alleen maar sinussen, want die zijn nou eenmaal nul bij x = 0.
Maar dat hoeft natuurlijk niet. Er zijn genoeg periodieke functies die niet nul zijn bij x = 0 en x = L dus die je nooit met sinussen kunt benaderen of omschrijven.

De oplossing is eenvoudig:
         
Gebruik ook cosinussen!
         
Ofwel; neem voor u(x) de volgende, meest algemene vorm:
         

         
We hebben al gezien hoe we al die an kunnen berekenen. De berekening van c en bn  gaat (gelukkig maar) ongeveer hetzelfde!
       
De berekening van c is het allereenvoudigst;  Integreer de functie u(x) gewoon over ้้n hele periode en al die sinussen en cosinussen vallen weg, zodat alleen c • 2L overblijft.

Voor de berekening van de bn gebruik je dezelfde truc als bij de an  maar nu met cosinussen in plaats van sinussen.
Dus om bn te berekenen vermenigvuldig je u(x) met  cos(nπx/L)  en als je dan over een hele periode integreert, dan vallen alle termen weg, behalve die met  bn.

Samengevat:
       

Fourieranalyse, voor een functie met periode 2L:

 

 

 

 

   
       
 

ฉ h.hofstede (h.hofstede@hogeland.nl)