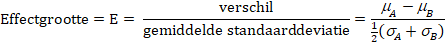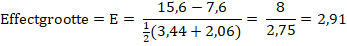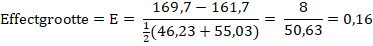| |
|
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Examenopgave Havo, Wiskunde A, 2018. |
| |
|
|
|
| |
Bij een bloedonderzoek worden het hemoglobinegehalte
en de hoeveelheid rode bloedcellen gemeten. In de uitslag van het
onderzoek staan van beide de gemeten waarden. Om deze uitslag te
kunnen beoordelen, worden de gemeten waarden vergeleken met de
bijbehorende referentiewaarden. Dit zijn de waarden zoals ze
gevonden worden bij 95% van de gezonde mensen. In deze opgave
bekijken we de referentiewaarden van volwassenen.
Het hemoglobinegehalte wordt uitgedrukt in millimol
per liter (mmol/L) (een mol is een eenheid voor het aantal deeltjes)
en de hoeveelheid rode bloedcellen in biljoenen per liter (1 biljoen
= 1012). We gaan ervan uit dat het hemoglobinegehalte en de
hoeveelheid rode bloedcellen van gezonde mannen normaal verdeeld
zijn. Dit geldt ook voor het hemoglobinegehalte en de hoeveelheid
rode bloedcellen van gezonde vrouwen.
In de tabel staan de referentiewaarden van het
hemoglobinegehalte en van de hoeveelheid rode bloedcellen. Deze
referentiewaarden liggen symmetrisch om het gemiddelde. Zo kun je in
de tabel bijvoorbeeld aflezen dat 95% van de gezonde mannen een
hemoglobinegehalte heeft tussen 8,6 mmol/L en 11,0 mmol/L. |
| |
|
|
|
| |
| |
geslacht |
referentiewaarden |
| hemoglobine |
man |
8,6 - 11,0 |
| |
vrouw |
7,6 - 10,0 |
| rode bloedcellen |
man |
4,4 - 5,8 |
| |
vrouw |
4,0 - 5,3 |
|
| |
|
|
|
| |
a. |
Bereken de standaardafwijking van de hoeveelheid
rode bloedcellen van gezonde vrouwen. Geef je antwoord in biljoenen
per liter en rond af op één decimaal. |
| |
|
|
|
| |
De standaardafwijking van het hemoglobinegehalte van
zowel gezonde mannen als gezonde vrouwen is 0,6 mmol/L. |
| |
|
|
|
| |
b. |
Bereken met behulp van het formuleblad of het
verschil tussen het hemoglobinegehalte van gezonde mannen en gezonde
vrouwen gering, middelmatig of groot is. |
| |
|
|
|
| 2. |
Examenopgave Havo. Wiskunde A, 2018. |
| |
|
|
|
| |
Een lunchrestaurants probeert
zijn klanten bewust te maken van de hoeveelheid kcal die ze
bestellen. Dit restaurant presenteert daarom de calorie-informatie
duidelijk zichtbaar bij het
bestelpunt. Onderzoekers hebben aan de klanten van dit restaurant
gevraagd of deze informatie effect had op hun bestelling. Die
informatie hebben zij per klant gekoppeld aan zijn of haar
kassabonnetje. De resultaten staan in de volgende tabel. |
| |
|
|
|
| |
| |
aantal
kassabonnetjes |
aantal kcal |
percentage
dat meer
dan 1000
kcal
bestelt |
| gemiddelde |
standaardafwijking |
calorie-
informatie
wel
gelezen |
568 |
713 |
301 |
17,5 |
calorie-
informatie
niet
gelezen |
1237 |
766 |
584 |
23,0 |
|
| |
|
|
|
| |
Op grond van de resultaten in deze tabel bespreken de
onderzoekers de volgende stelling: ‘Er bestaat een groot verschil in
het aantal kcal per bestelling tussen klanten die de
calorie-informatie wel hebben gelezen en klanten die de
calorie-informatie niet hebben gelezen.’
Onderzoek of deze
stelling door de gegevens in deze tabel wordt ondersteund. |
| |
|
|
|
| 3. |
Examenopgave Havo, Wiskunde A, 2018. |
| |
|
|
|
| |
De Jamuna is een van de grootste
rivieren van Bangladesh. In het regenseizoen kan de rivier
wel bijna 12 km breed zijn. Op een bepaalde plaats van de Jamuna wordt
gemeten hoeveel water (in m3)
daar per seconde langs stroomt. Dit noemt men de
waterdoorvoer. Deze varieert behoorlijk: in het
regenseizoen kan de waterdoorvoer wel 100 000 m3
per seconde zijn,
terwijl de waterdoorvoer in de droge tijd ‘slechts’ 3000 m3
per seconde is.
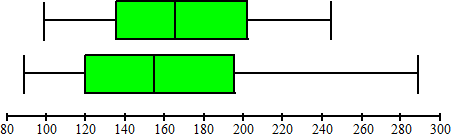
Er is berekend hoe groot de waterdoorvoer in
de maand januari van 1972 gemiddeld was. Dit werd ook gedaan
voor alle andere januarimaanden in de periode 1973 tot en
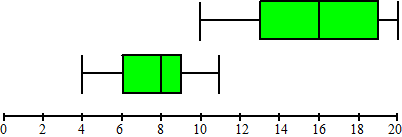
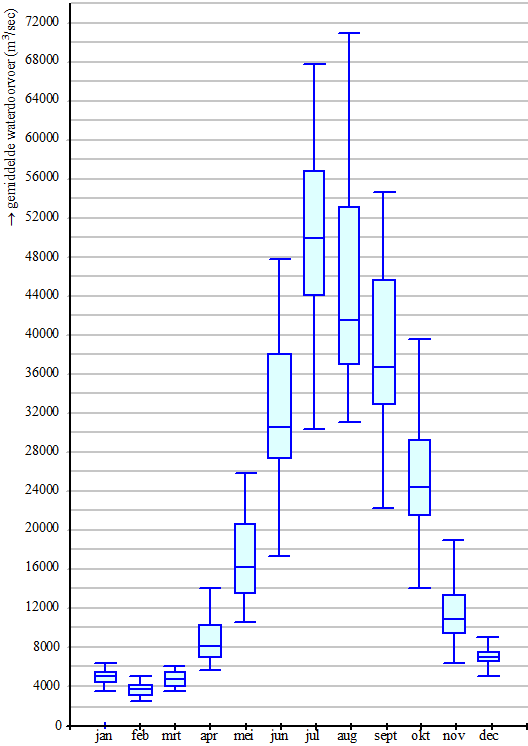
met 2007. Deze 36 waarden zijn samengevat met een boxplot.
Deze boxplot staat in de figuur hieronder.
In diezelfde figuur staat ook een boxplot die hoort bij alle
februarimaanden in de periode 1972 tot en met 2007. En net
zo voor alle andere maanden in het jaar. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Karin doet met behulp van het
formuleblad de volgende uitspraak: “Het verschil in
gemiddelde waterdoorvoer tussen de julimaanden en de
augustusmaanden in de periode 1972 tot en met 2007 is
gering.” |
| |
|
|
|
| |
a. |
Is deze uitspraak juist, onjuist, of is dat
niet uit de figuur hierboven af te leiden? Licht je
antwoord toe. |
| |
|
|
|
| |
Bob doet ook een uitspraak: “In april 1983
was de gemiddelde waterdoorvoer groter dan in februari
1983.” |
| |
|
|
|
| |
b. |
Is deze uitspraak juist, onjuist, of is dat
niet uit de figuur hierboven af te leiden? Licht
je antwoord toe. |
| |
|
|
|
| 4. |
Examenopgave Havo, Wiskunde A, 2017 |
| |
|
|
|
| |
In een bedrijf wordt er gewerkt in drie
ploegendiensten.
Tijdens elke dienst komen er storingen voor. Het
productieproces wordt dan een aantal minuten stilgelegd totdat de
storing verholpen is. Telkens wordt bijgehouden hoe lang de storing
duurt. Na afloop van de dienst wordt de totale tijd van alle
storingen genoteerd. Deze tijd noemt men de uitvaltijd. De
directie wil dat de uitvaltijd zo klein mogelijk is.
Om te onderzoeken hoe groot de uitvaltijd is, heeft
men van 16 werkweken van elk van de drie verschillende ploegendiensten de gemiddelde uitvaltijd en de standaardafwijking berekend. Zie
de volgende tabel. |
| |
|
|
|
| |
| uitvaltijd per dag- of
nachtdienst in minuten |
| |
gemiddelde |
standaardafwijking |
| dagdienst A |
36,75 |
1,10 |
| dagdienst B |
37,29 |
1,04 |
| nachtdienst |
29,39 |
1,53 |
|
| |
|
|
|
| |
Men vermoedt dat de lagere uitvaltijden tijdens de
nachtdiensten te maken hebben met het feit dat de energietoevoer
gedurende de nacht constanter is dan overdag. Daarom wordt de
energietoevoer overdag verbeterd.
Na verloop van tijd blijkt dat de gemiddelde
uitvaltijd van de A-diensten en B-diensten gelijk geworden is aan de
gemiddelde uitvaltijd van de nachtdiensten. De
standaardafwijkingen van de A-diensten en B-diensten zijn niet
veranderd.
Bereken voor
dagdienst B of het verschil in uitvaltijd tussen de oude en de
nieuwe situatie groot, middelmatig of gering is. |
| |
|
|
|
| 5. |
Examenopgave Havo, Wiskunde A, 2016 Jaarlijks wordt voor een onderzoek aan een groot aantal
personen gevraagd hun lengte te schatten. We noemen deze lengte de
geschatte lengte. Daarnaast wordt de lengte nauwkeurig door een
onderzoeker gemeten. We noemen deze lengte de werkelijke lengte.
De geschatte lengte en de werkelijke lengte worden vervolgens met elkaar
vergeleken. Het blijkt dat mensen in het algemeen hun lengte te hoog
schatten.
In het onderzoek van een bepaald jaar schatten de
vrouwen hun lengte gemiddeld 0,9 cm hoger dan hun werkelijke lengte. De
standaardafwijking van de werkelijke lengte was 6,0 cm. De
standaardafwijking van de geschatte lengte was 6,2 cm.
Bepaal of het verschil tussen de werkelijke lengte en de geschatte lengte
gering, middelmatig of groot is. |
| |
|
|
| 6. |
Examenopgave Havo, Wiskunde A, 2021-III In de tabel
hieronder zie je de
resultaten van een enquête die door een middelbare school is
gehouden onder de ouders. Je ziet de resultaten op de stelling
"De schoolregels zijn duidelijk" die in 2018 op die school door 700 leerlingen en 500 ouders
beantwoord is. |
| |
|
|
|
| |
| stelling: "De
schoolregels zijn duidelijk" |
| |
leerlingen |
ouders |
| zeer oneens |
7 (1%) |
10 (2%) |
| oneens |
7 (1%) |
15 (3%) |
| zowel eens als oneens |
49 (7%) |
60 (12%) |
| eens |
343 (39%) |
225 (45%) |
| zeer eens |
294 (42%) |
190 (38%) |
|
| |
|
|
|
| |
Met behulp van
het formuleblad kun je nagaan dat het verschil tussen de leerlingen
en de ouders bij deze stelling gering is. Als er meer ouders hadden
gekozen voor ‘zowel eens als oneens’ in plaats van ‘eens’, dan zou
het verschil tussen de leerlingen en de ouders groter zijn.
Bereken het
minimale aantal ouders dat voor ‘zowel eens als oneens’ in plaats
van ‘eens’ had moeten kiezen, zodat het verschil tussen de
leerlingen en de ouders niet meer gering zou
zijn, maar minstens middelmatig. |
| |
|
|
|
| |
|
|
|
|
7. |
Het gebruik van mobiele telefoons onder middelbare scholieren
loopt de laatste jaren nogal uit de hand. Onderzoeksbureau
Zorgfocuz probeert in opdracht van de gemeente Het
Hogeland aan de hand van een enquête onder 4500 scholieren een
beeld te krijgen van de tijd die gemiddeld op de telefoon wordt
doorgebracht.
Men onderscheidt daarbij 3 leeftijdsgroepen, namelijk 10-12
jaar, 13-15 jaar en 16-18 jaar.
Men ontdekte dat de telefoontijd normaal verdeeld is met de
volgende gegevens: |
 |
| |
|
|
|
| |
|
leeftijd |
Gemiddelde telefoontijd (in minuten per dag) |
Standaardafwijking
(in minuten) |
Aantal deelnemers in de steekproef |
|
10-12 |
206 |
10 |
1280 |
|
13-15 |
234 |
20 |
1415 |
|
16-18 |
248 |
20 |
1805 |
|
| |
|
|
|
| |
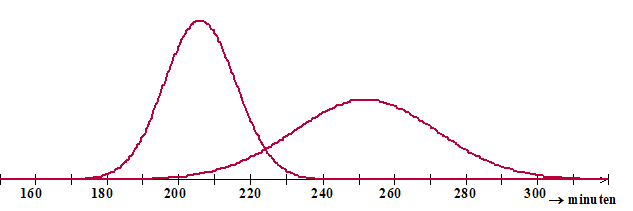
In
het rapport verschenen drie normale verdelingen om deze gegevens
te beschrijven.
Hier onder zie je de verdelingen van de 10-12 en van de 16-18
jarigen. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Schets zo nauwkeurig mogelijk in de figuur van het werkblad de
normale verdeling van de 13-15 jarigen. |
| |
|
|
|
| |
b. |
Hoeveel procent van de 10-12 jarigen had een gemiddelde
telefoontijd tussen de 206 en 226 minuten per dag? |
| |
|
|
|
| |
c. |
Bereken aan de hand van deze gegevens of het verschil tussen de
10-12 jarigen en de 16-18 jarigen gering, middelmatig
of groot is. |
| |
|
|
|
| |
d. |
Geef met de gegevens uit deze steekproef een
95%-betrouwbaarheidsinterval voor de gemiddelde telefoontijd van
de 13-15 jarigen in Nederland. |
| |
|
|
|
|
8. |
Ondanks het verbod dit jaar op vele soorten vuurwerk is er toch
nog erg veel vuurwerk verkocht. Deels illegaal en deels legaal.
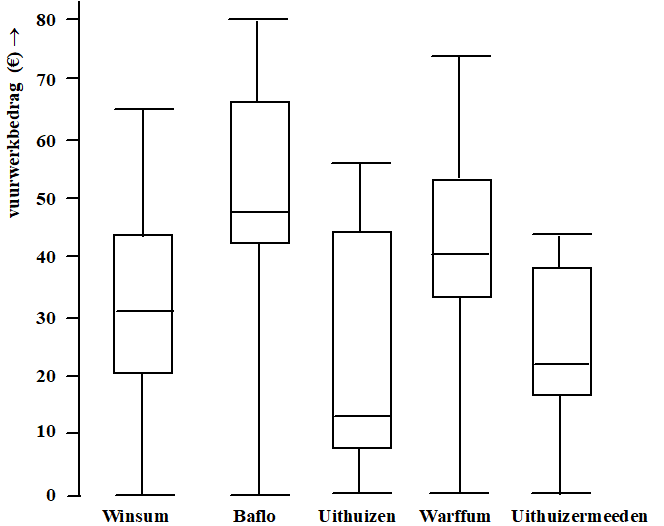
Een onderzoek in vijf plaatsen in Noord-Groningen naar hoeveel
geld men aan vuurwerk heeft besteed levert de vijf boxplots
hieronder op. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Welke plaats heeft de grootste spreidingsbreedte? Leg duidelijk
uit. |
| |
|
|
|
| |
b. |
Welke plaats heeft de grootste kwartielafstand? Leg duidelijk
uit |
| |
|
|
|
| |
c. |
Zijn er plaatsen waartussen het verschil wiskundig gezien
klein genoemd kan worden? Zo ja welke? Geef een
duidelijke uitleg. |
| |
|
|
|
| |
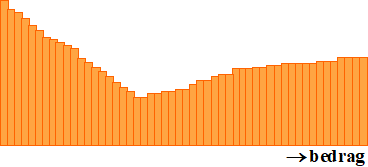
d. |
Bij welk van de plaatsen zou het histogram hieronder kunnen
horen?
Leg duidelijk uit waarom |
| |
|
|
| |
|
 |
| |
|
|
|
|
9. |
Het is voor websites als YouTube erg belangrijk dat kijkers lang
genoeg naar een reclame kijken, en niet direct wegzappen.
Immers: hoe langer men kijkt, des te meer inkomsten zal de
adverteerder hebben dus des te meer adverteerders willen hun
advertenties graag op YouTube zetten.
Hieronder zie je twee beelden uit filmpjes van de concurrerende
make-up merken Rimmel London en Maxfactor. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
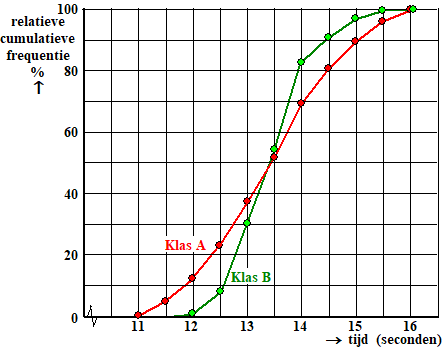
Op internet kun je natuurlijk makkelijk bijhouden hoe lang men
gemiddeld naar een filmpje kijkt.
Dat heeft men voor deze twee reclamefilmpjes (van elk 60
seconden) gedaan en dat gaf de volgende tabel: |
| |
|
|
|
| |
|
Kijktijd
(in seconden) |
aantal
bezoekers |
|
Rimmel
London |
Maxfactor |
|
0 - < 5 |
834 |
68 |
|
5 - < 10 |
821 |
156 |
|
10 - < 15 |
764 |
294 |
|
15 - < 20 |
732 |
481 |
|
20 - < 30 |
535 |
1430 |
|
30 - < 40 |
132 |
1412 |
|
40 - < 50 |
45 |
764 |
|
50 - 60 |
24 |
231 |
|
|
|
|
|
Totaal |
3887 |
4836 |
|
| |
|
|
|
| |
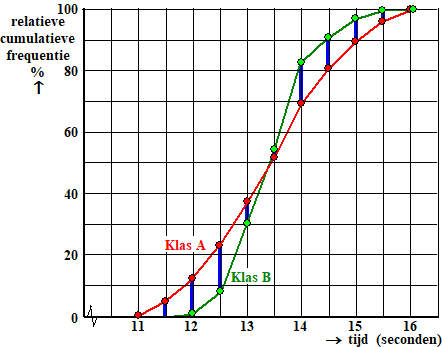
a. |
Bereken met Max Vcp of het verschil in kijktijd tussen deze twee
filmpjes gering, middelmatig of groot
is. |
| |
|
|
|
| |
De
verdeling van Maxfactor ziet er aardig symmetrisch uit en die
van Rimmel London juist niet. |
| |
|
|
|
| |
b. |
Hoe noemen we een verdeling die de vorm van die van Rimmel
London heeft? |
| |
|
|
|
| |
Het zou dus heel goed kunnen dat de verdeling van Maxfactor een
normale verdeling is. |
| |
|
|
|
| |
c. |
Bereken de standaardafwijking en het gemiddelde van de getallen
van Maxfactor en onderzoek of de vuistregel van 68% ongeveer
voor deze verdeling zou kunnen gelden. |
| |
|
|
|
| 10. |
De Wiskunde
Kangoeroe is een reken-en wiskundewedstrijd voor basis- en
middelbare scholen.
In 1980 werd in Australië voor het eerst zo'n soort
wiskundewedstrijd georganiseerd. Het succes inspireerde enkele
Franse wiskundigen om ook zoiets te doen. In de zomer van 1994
is de organisatie van de Kangoeroe in Frankrijk gestart. Als
eerbetoon noemden ze hun wedstrijd Kangourou. In
Nederland heet de wedstrijd Wereld Wijde Wiskunde Wedstrijd
Kangoeroe, afgekort tot W4 Kangoeroe.
In 2016 deden er 6,5 miljoen scholieren mee uit 60 landen.
WizBrain is de versie voor leerlingen van klas 1
en 2 van HAVO/VWO.
In onderstaande tabel zie je de resultaten uit 2020 van de
deelnemers aan WizBrain uit België en Nederland, gesplitst naar
jongens en meisjes. |
 |
| |
|
|
|
| |
|
|
meisjes |
jongens |
|
|
gemiddelde
score |
standaard
afwijking |
aantal
deelnemers |
gemiddelde
score |
standaard
afwijking |
aantal
deelnemers |
|
België |
68 |
19 |
456 |
59 |
14 |
621 |
|
Nederland |
65 |
20 |
832 |
51 |
12 |
460 |
|
| |
|
|
|
| |
We hebben hier onder anderen te maken met de variabelen
"geslacht" (meisje-jongen) en "land" (België-Nederland). |
| |
|
|
|
| |
a. |
Zijn deze variabelen nominaal of ordinaal? Leg duidelijk uit
waarom. |
| |
|
|
|
| |
b. |
Als je niet naar de scores zelf kijkt, maar alleen maar naar de
aantallen jongens en meisjes die deelnamen, is het verschil in
jongens en meisjes tussen Nederland en België dan
gering, middelmatig of groot? |
| |
|
|
|
| |
c. |
Is
het verschil tussen de gemiddelde scores van de meisjes en van
de jongens in Nederland gering, middelmatig, of
groot? |
| |
|
|
|
| |
Hieronder zie je vier frequentiepolygonen van de scores van de
meisjes uit vier verschillenden landen.
Eén van die vier frequentiepolygonen gaat over de meisjes uit
Nederland. |
| |
|
|
|
| |
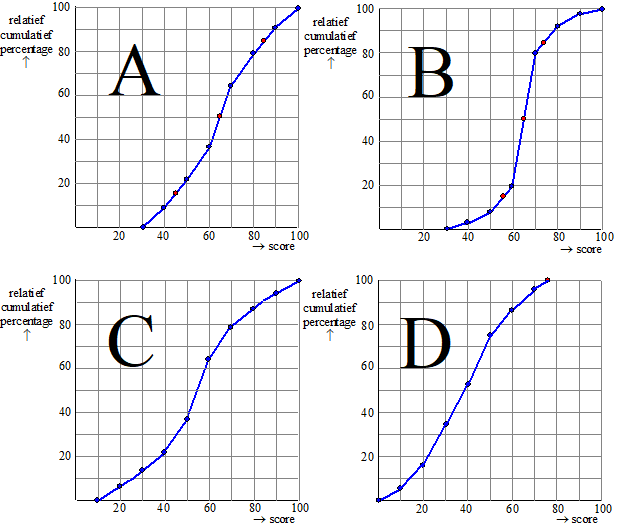 |
| |
|
|
|
| |
d. |
Leg duidelijk uit welk frequentiepolygoon klopt met het gegeven
gemiddelde én de standaardafwijking van de meisjes in Nederland. |
| |
|
|
|
| |
e. |
Bepaal met behulp van boxplots of de verschillen tussen de
scores uit de diagrammen C en D gering, middelmatig
of groot zijn. |
| |
|
|
|
 |
 |