Formules zelf opstellen..

© h.hofstede (h.hofstede@hogeland.nl)
   
Als je een geval hebt waarin een hoek varieert, of nog onbekend is, dan kun je die hoek natuurlijk gewoon een letter geven  (meestal worden Griekse letters voor hoeken gebruikt), en dan met die letter proberen een formule te maken.
Zo'n formule (met een onbekende hoek erin) kun je dan weer gebruiken om met algebra berekeningen te maken.

Mooi toch? Een combinatie van algebra en meetkunde.

Niet zoveel theorie deze les, je moet vooral zelf oefenen. Een voorbeeldje.

Voorbeeld.

Hiernaast staat een bovenaanzicht van een plank in een gang.
De plank moet door de gang van A naar B worden gebracht. Daarbij moet hij horizontaal blijven (je mag hem niet schuinzetten).
Hiernaast zie je een situatie waarbij de plank precies past (klemstaat in de gang). 

Twee vragen:

a.  Stel een formule op voor de lengte van de plank als functie van hoek α.
b.  Wat is de langste plank die door de gang kan?

Oplossing:

Hiernaast zie je de figuur nogmaals met wat meer letters erin.

Maar eens wat formules opstellen dan:
L = L1 + L2
cosα = 2/L1 ⇒   L1 = 2/cosα
sinα = 3/L2  ⇒   L2 = 3/sinα

Daaruit volgt dat  L = 2/cosα + 3/sinα
En daar is het antwoord op vraag a) al.

 
De langste plank die nog door de gang kan is gelijk aan de kleinste waarde van L die uit de formule kan komen.
Immers bij die waarde van α kan een langere plank er niet door. En bij het draaien van de plank zal die waarde van α toch echt voorkomen.
We zoeken dus het minimum van de L-formule.
Nou, daar is een GR voor.
Voer de L-formule in bij Y1 (met X = α) en bereken het minimum met calc - minimum.

   
Daar zien we dat de langste plank die door de gang kan 7,02 meter is, en dat de kritieke situatie ontstaat bij α = 48,9º.
   
OPGAVEN
   
1.

       
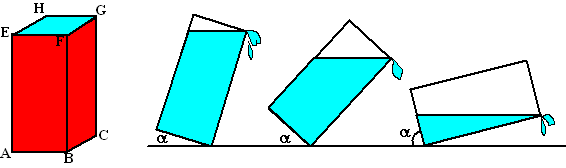
  Een kan van 20 bij 20 bij 30 cm (hoogte) is gevuld met water.
De kan wordt gekanteld om ribbe BC en het water stroomt daardoor weg langs de rand FG.
De hoek waarover is gedraaid noemen we α . In de figuur hierboven zie je de kan met daarnaast een aantal vooraanzichten.
       
  a. Hoeveel liter water is er voor een hoek α van 20° weggestroomd?
     

1,456
  b. Voor de hoeveelheid water V (in liter) in de bak blijkt bij de eerste twee getekende vooraanzichten te gelden:
V = 12 - 4·tanα.
Toon dit aan.
       
  c. Welke formule hoort er bij V voor α groter dan in de laatst getekende situatie?
     

V = 12 - 9/tanα
       
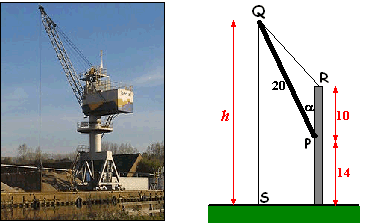
2. Hieronder zie je een foto van een hijskraan om grind en zand over te slaan met daarnaast een schematische tekening.
       
 

       
  De arm PQ kan in horizontale richting draaien om punt P.
Verder kan, door kabel QR langer of korter te maken, de arm PQ ook in het vlak van de tekening draaien om punt P. Daardoor komt punt Q hoger of minder hoog boven de grond.
De afmetingen zijn zoals aangegeven in de figuur (in meters)
Noem de hoogte van P boven de grond gelijk aan h.
       
  a. Bereken h als α = 50º
     

26,36
  b. Stel een formule op voor h als functie van α.
     

h = 14+20cosα
  c. Bereken de lengte van kabel QR als α = 20º
     

11,14
  d. Stel een formule op voor QR als functie van α voor α < 60º.
     

√(500-400cosα)
       
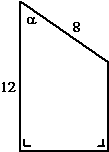
3. Druk de oppervlakte van de figuur hiernaast uit in α.

     

96sinα+32sinαcosα
       
4. Van een dakgoot goot is de breedte van de bodem 40 cm en de lengte van de opstaande zijwanden 20 cm.
Een dwarsdoorsnede staat in de figuur hiernaast.
De oppervlakte (O) van zo'n dwarsdoorsnede hangt af van de hellingshoek α van de opstaande wanden.
Voor deze oppervlakte O blijkt te gelden:

     
 

O = 400sinαcosα + 800sinα

  
       
  a. Toon aan dat deze formule juist is.  
       
  b. Bepaal de maximale oppervlakte van zo'n doorsnede.  
     

880,73
       
5. Examenopgave (deels)
 

       
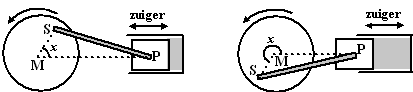  Een zuiger is door middel van een drijfstang verbonden met een draaiende schijf. Als de schijf draait beweegt de zuiger horizontaal heen en weer.
M is het middelpunt van de schijf, S is het (scharnierende) verbindingspunt van de drijfstang en de schijf. Bij punt P is de drijfstang ook scharnierend met de zuiger verbonden. MS = 1  en  PS = 4.
Stel de grootte van de hoek PMS gelijk aan x graden.
De afstand PM is afhankelijk van de hoekgrootte x;  stel PM = a(x)

Voor iedere hoekgrootte x geldt:  a(x) = cosx + √(16 - sin2x)
       
  a. Bewijs deze formule voor  0 < x < 90º.  
       
  b. Het minimum  van a(x) is gelijk aan 3 en het maximum is gelijk aan 5. Leg duidelijk uit hoe je dat kunt beredeneren met de figuur hierboven.
       
  c. Bij één rondgang van de schijf zal de lengte PM op twee momenten gelijk zijn aan de lengte van de drijfstang PS.  Hoe groot zijn de hoeken x waarbij zich dat voordoet? Geef een algebraïsche berekening.
     

82,8 en 277,2
       
6. Examenopgave (deels) HAVO Wiskunde B, 1996
 

       
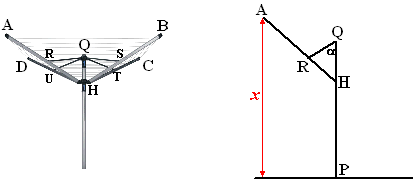
  In de figuur hierboven links is het metalen geraamte van een droogmolen getekend.
Getekend zijn:
•  de verticale drager PQ.
•  de even lange armen HA, HB, HC en HD
•  de even lange staven QR, QS, QT en QU
De punten R, S, T en U hebben dezelfde afstand tot H.
Afmetingen in cm:  PQ = 200, QR = 40, AR = 120 en HR = 60.

In H zit een ringvormige Huls om de drager. Deze huls kan schuiven langs de drager en met een schroefje op elke hoogte worden vastgeklemd. De hoogte van H ten opzichte van de grond is dus variabel. Alle overige verbindingen tussen twee onderdelen zijn zo gemaakt dat die onderdelen alleen maar ten opzichte van elkaar kunnen draaien.

Als de huls langs de drager wordt geschoven verandert de stand van de armen. Daardoor verandert de hoogte van de vrije uiteinden A, B, C en D.

Vat in deze opgave drager, armen en staven op als lijnstukken en de huls en overige verbindingen als punten.
a is de hoek in graden die de staaf RQ maakt met de draaier PQ. De hoogte (in cm) van het vrije uiteinde A van de arm HA ten opzichte van de grond noemen we x. Zie de rechter figuur hierboven.

Er zijn twee standen waarbij de molen geheel is dichtgeklapt (zodat de armen verticaal omhoog staan)

       
  a. Bereken de bijbehorende waarden van x.  
     

360 en 280
  b. Bereken x in gehele cm nauwkeurig als α = 30º
     

278
  De afstand van R tot PQ kan x in α worden uitgedrukt en met behulp van die afstand kan het verband tussen x en α gevonden worden.
Voor 0 < α < 180º  geldt de formule:  x =  200 - 40cosα + 40√(9 - 4sin2α)
       
  c. Toon de juistheid van deze formule aan voor  0 < α < 90º.
       
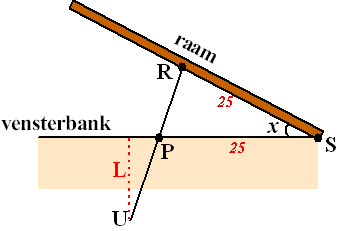
7. Een open raam kan met een raamuitzetter worden vastgezet. In de figuur hieronder zie je het bovenaanzicht van een raamuitzetter UR die in punt R scharnierend aan het raam is bevestigd.
RS = PS = 25 cm  en UR = 50 cm.
De afstand L van punt U tot lijn SP hangt af van hoek x.
       
 

       
  a. Neem x = 20° en bereken L  
     

41,16
  b. Voor L geldt de formule:  L = 50 · cos0,5x · (1 - sin0,5x)
Toon aan dat deze formule juist is.
       
8. examenvraagstuk HAVO Wiskunde B, 1994.
       
 

       
 

       
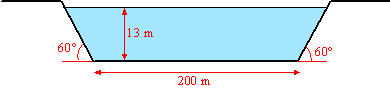
  Om scheepvaart mogelijk te maken mag de stroomsnelheid van het water maximaal 3 m/s bedragen.
       
  a. Bereken voor de situatie van bovenstaande figuur hoeveel m3 water het kanaal per seconde zou doorlaten bij een stroomsnelheid van 3 m/s en een waterhoogte van 13 meter. Rond het antwoord af op een geheel getal.
       
  Volgens waterbouwkundigen zijn drie factoren van invloed op de stroomsnelheid van het water in een kanaal:  de hydraulische straal, het verhang en de remmende werking van oevers en bodem. Hieronder worden deze begrippen nader toegelicht.

Voor de berekening van de hydraulische straal R heb je de 'natte oppervlakte'  en de 'natte omtrek' nodig. Bekijk daartoe het dwarsprofiel in de onderstaande figuur.

       
 

       
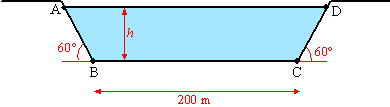
  De 'natte oppervlakte' is de oppervlakte van vierhoek ABCD.
De 'natte omtrek' is de totale lengte van de lijnstukken in dit dwarsprofiel die de afscheiding vormen tussen grond en water:  AB + BC + CD.

De hydraulische straal is het quotiënt van de natte oppervlakte en de natte omtrek.  In formulevorm:
       
 

       
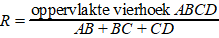  In de figuur hierboven kan R opgevat worden als functie van de waterhoogte h in meters.
       
  b. Laat zien dat in die situatie bij benadering de volgende formule geldt:
     
       
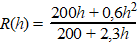9. examenopgave HAVO Wiskunde B, 1995.
       
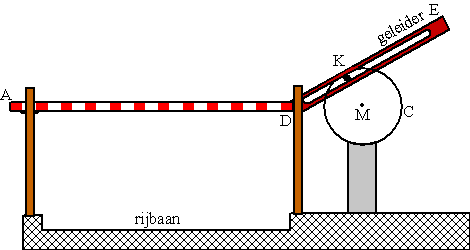
  De uitgang van een parkeergarage wordt afgesloten door een slagboom. Deze bestaat uit een rood-wit gekleurde balk AD, waaraan onder een vaste hoek ADE een geleider DE is gemonteerd. Deze geleider is een beugel met een gleuf. Zie de volgende figuur.
       
 

       
  Als de cirkelschijf C draait, beweegt een metalen knop K die op de cirkelschijf gemonteerd is, heen en weer door die gleuf.
Tegelijkertijd trekt knop K in zijn baan om M de beugel DE omlaag, zodat de rood-witte balk AD om het draaipunt D open draait. Bij doordraaien van cirkelschijf C trekt K vanaf een gegeven moment de beugel DE weer omhoog, zodat AD weer dicht gaat. Zie ook de afbeeldingen in de figuren hier onder. In deze opgave worden balk en beugel opgevat als lijnstukken.
       
 

       
  Middelpunt M en draaipunt D liggen even hoog.
Gegeven is verder:  DM = 30 cm en KM = 20 cm.
       
  a. Bereken in graden nauwkeurig de hoek ADE.
       
 

       
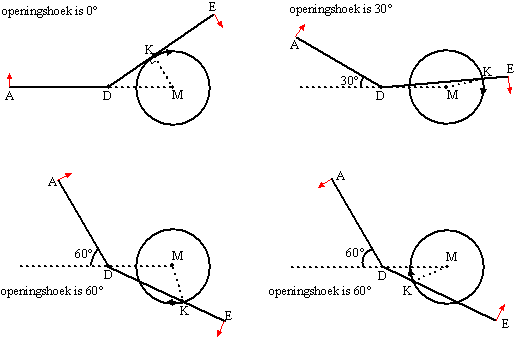
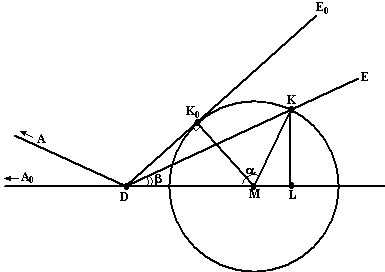
  In de ruststand (met horizontale slagboom) bevindt K zich in positie K0 (zie de figuur). Bij een willekeurige positie van K noemen we ∠DMK = α  en  ∠MDK = β. De projectie van K op de lijn DM noemen we L.  
       
  b. Teken de positie van DE en K in het geval dat de slagboom zo ver mogelijk open is. Licht je werkwijze toe.
       
  c. Bereken de maximale openingshoek van de slagboom in graden nauwkeurig.
       
  d. Toon aan dat zowel voor  0º < α < 90º als voor  90º < α < 180º geldt:  DL = 30 - 20cosα.
       
  Voor het verband tussen de hoeken α en β geldt:
 
       
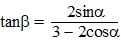  e. Leid deze formule af. Je mag je hierbij beperken tot het geval 90º < α < 180º
       
10.

       
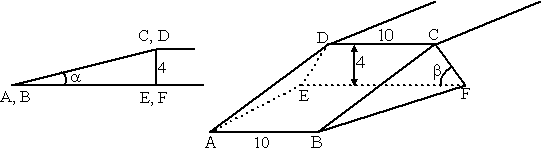
  Een oprit van een viaduct heeft een hellingshoek α, met α < 90º (zie zijaanzicht in de figuur). De viaducthoogte is 4 m en de wegbreedte is 10 m. In de figuur rechtsboven is in parallelprojectie een model van zo'n oprit getekend (niet op schaal). De oprit loopt aan de zijkanten schuin af naar beneden, maar vlak EFCD is verticaal.
Vierhoek EFCD is in de figuur rechtsboven evenwijdig aan het tafereel getekend, is een gelijkbenig trapezium; hierin is  ∠CFE = β, met β < 90º.
       
  a. Teken in de figuur rechtsboven het punt G op EF waarvoor geldt dat ∠CBG = α. Licht je werkwijze toe.
       
  De hoeveelheid zand (in m3) die nodig is voor het aanleggen van de oprit noemen we V.
V kan worden uitgedrukt in α en β door:
 

       
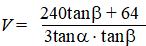  b. Toon dit aan.  
       
11. Examenvraagstuk VWO Wiskunde B, 2003

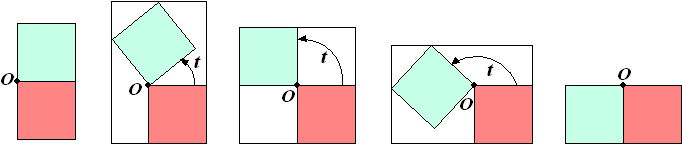
Twee vierkanten, beide met zijde 1, hebben het hoekpunt O gemeenschappelijk. Het onderste vierkant ligt vast. Het bovenste vierkant wordt om O gedraaid; t is de draaihoek in radialen. In de figuur hieronder zijn tussen de begin- en eindstand drie tussenstanden getekend. Om de twee vierkanten is steeds een zo klein mogelijke rechthoek getekend, met twee zijden langs het vaste vierkant.
       
 

       
  De oppervlakte R van de omhullende rechthoek is een functie van de draaihoek t.

     
  a. Bereken de oppervlakte van R voor  t = 1/4π
   

2 + 1,5√2
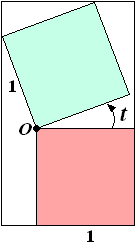
  Voor elke waarde van t tussen 0 en 1/2p geldt: 
R(t) = (1 + sint)•(1 + sint + cost)
In de figuur hiernaast is de situatie getekend voor een waarde van t tussen 0 en 1/2π.
     
  b. Toon de juistheid van de formule aan voor elke waarde van t tussen  0 en 1/2π.
       
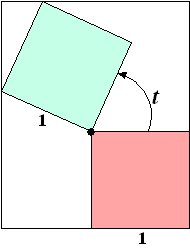
  Er zijn tussen de begin- en de eindstand twee posities van de vierkanten waarvoor R(t) maximaal is. In de figuur hiernaast is één van die posities getekend.

     
  c. Teken in deze figuur de andere positie van de vierkantjes waarvoor R(t) maximaal is. Licht je werkwijze toe.
       
     

© h.hofstede (h.hofstede@hogeland.nl)