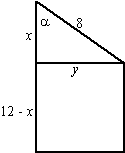|
|||||
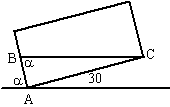
| 1. | a. |
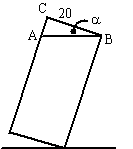
α =
20º geeft tan20 = AC/20
⇒ AC = 20 tan20 = 7,28 de oppervlakte van ABC is dan 1/2 7,28 20 = 72,8 de inhoud van het weggestroomde water is dan 72,8 20 = 1456 cm3 dat is 1,456 liter. |
|
||
| b. | Hetzelfde verhaal als hierboven
maar nu met a ipv 20: AC = 20 tanα opp ABC is 1/2 20 tanα 20 = 200tanα inhoud van het weggestroomde water is 200tanα 20 = 4000 tanα cm3 dat is 4tanα liter Dan blijft er 12 - 4tanα liter over in de bak. |
||||
| c. | tanα =
30/AB ⇒ AB =
30tanα de oppervlakte van ABC is dan 1/2 30tanα 30 = 450tanα De inhoud van het water in de bak is dan 450tanα 20 = 9000tanα cm3 Dus V = 9tanα liter |
 |
|||
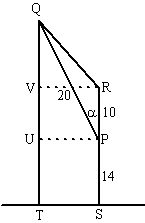
| 2. | a. | als
α
= 50º dan is ∠UPQ = 40º sin40º = UQ/20 ⇒ UQ = 20 sin40º = 12,86 h = 14 + 12,86 = 26,86 |
|
||
| b. | ∠PQU =
α (Z-hoeken) cosα = QU/20 ⇒ QU = 20cosα h = 14 + 20cosα |
||||
| c. | QR2 = 202 +
102 - 2 20 10 cos20º = 124,12 QR = √124,12 = 11,14 meter |
||||
| d. | QR2 = 202 +
102 - 2 20 10 cosα QR2 = 500 - 400cosα QR = √(500 - 400cosα) |
||||
| 3. | cosα
= x/8 ⇒
x = 8cosα sinα = y/8 ⇒ y = 8sinα de driehoek heeft oppervlakte 1/2 xy = 1/2 8cosα 8sinα = 32sinαcosα de rechthoek heeft oppervlakte y(12 - x) = 8sinα(12 - 8cosα) = 96sinα - 64sinαcosα samen geeft dat 32sinαcosα + 96sinα - 64sinαcosα = 96sinα - 32sinαcosα |
|
|||
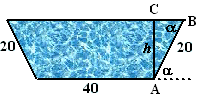
| 4. | a. | sinα =
h/20 ⇒
h = 20sinα cosα = BC/20 ⇒ BC = 20cosα driehoek ABC heeft oppervlakte 1/2 20sinα 20cosα = 200sinαcosα de rechthoek heeft oppervlakte 40 20sinα = 800sinα er zijn twee zulke driehoeken en één rechthoek, dus samen geeft dat: 400sinαcosα + 800sinα |
 |
||
| b. | Y1 = 400sin(X)cos(X)
+ 800sin(X) calc - macimum geeft een maximumoppervlakte van 880,73 (voor α = 68,53º) |
||||
| 5. | a. | sinx = ST/1
dus ST = sinx cosx = MT/1 dus MT = cosx TP2 = SP2 - ST2 = 16 - sin2x dus TP = √(16 - sin2x) a = MT + TP = cosx + √(16 - sin2x) |
 |
||
| b. | Als S helemaal links
van M op het verlengde van MP ligt is MP = PS - MS = 4 - 1 = 3 Als S helemaal rechts tussen M en P op lijnstuk MP ligt is MP = PS + MS = 4 + 1 = 5 |
||||
| c. | 4 = cosx +
√(16 - sin2x) 4 - cosx = √(16 - sin2x) (4 - cosx)2 = 16 - sin2x 16 - 8cosx + cos2x = 16 - (1 - cos2x) 8cosx = 1 cosx = 1/8 x = 82,8º of x = 277,18º |
||||
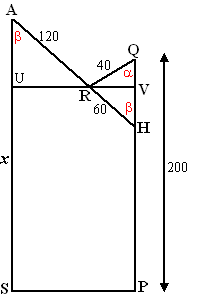
| 6. | a. | Helemaal ingeklapt: van de 120 AR steekt dan nog 120 - 40 = 80 boven Q uit (40 ligt langs QR) A ligt 80 boven Q dus h = PA = PQ + QA = 200 + 80 = 280 |
|
||
| b. | 60/sin30 =
40/sinβ sinβ = 40 sin30/60 = 1/3 Maar ∠RAU is ook gelijk aan β (Z-hoeken) sinRAU = UR/120 ⇒ UR = 120 1/3 = 40 AU = √(1202 - 402 ) = 113,1 cosa = QV/40 ⇒ QV = 40cosa = 40 cos30º = 34,6 Dan is x = AS = PQ - QV + AU = 200 - 34,6 + 113,1 = 278,5 |
||||
| c. | dezelfde berekening met a
ipv 30º: 60/sinα =
40/sinβ |
|
|||
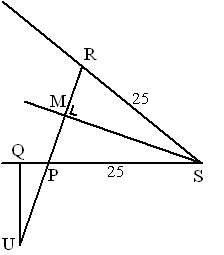
| 7. | a. | Driehoek RPS is gelijkbenig Teken de hoogtelijn SM vanuit S sin(10) = MP/25 ⇒ MP = 25 sin10 = 4,34 Dan is RP = 2 4,34 = 8,68 en UP = 50 - 8,68 = 41,32 ∠MPS = 80º = ∠UPQ sin80º = QU/PU = QU/41,32 QU = 41,32 sin80º = 40,7 cm |
 |
||
| b. | ∠PSM =
1/2x ∠SPM = 90º - 1/2x ∠UPQ = 90º - 1/2x ∠PUQ = 1/2x |
||||
| sinx = MP/25
⇒ MP = 25sin1/2x
⇒
PR = 50sin1/2x
⇒ UP = 50 - 50sin1/2x cos(PUQ) = cos(1/2x) = QU/UP QU = UP cos(1/2x) = (50 - 50sin1/2x) cos(1/2x) = 50 cos(1/2x) (1 - sin1/2x) |
|||||
| 8. |
|
||||
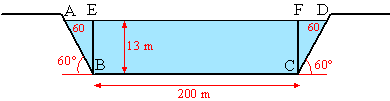
| a. | tan60 = EB/AE
⇒ AE = EB/tan60 = 13/√3
= 13/3√3 dan is de oppervlakte van de beide driehoeken ABE en DCF samen 13/3√3 13 = 169/3√3 de oppervlakte van rechthoek BCEF is 200 13/3√3 = 2600/3√3 samen geeft dat 923√3 dat zou bij 3 m/sec een hoeveelheid van 3 923√3 = 2769√3 m3 water geven dat is ongeveer 4796 m3 |
||||
| b. | AE = h/tan60
= 0,577h Oppervlakte beide driehoeken samen is 0,577h h = 0,577h2 Oppervlakte rechthoek is 200 h Natte oppervlakte is 0,577h2 + 200h ≈ 0,6h2 + 115h sin60 = 1/2√3 = h/AB ⇒ AB = h/0,5√3 = 1,15h Natte omtrek is AB + BC + CD = 2,3h + 200 op elkaar delen geeft de gevraagde formule. |
||||
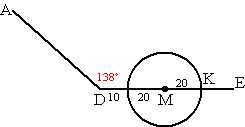
| 9. | a. | sinMDK = MK/MD
= 20/30 ⇒ MDK = 41,8º dan is ∠ADK = 180 - 41,8 = 138,2º ≈ 138º |
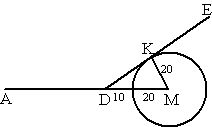 |
||
| b. | De slagboom is zo ver mogelijk
open als K op het verlengde van DM op de cirkel ligt. Zie de figuur hiernaast. ∠ADK = 138º |
 |
|||
| c. | De openingshoek in de situatie hierboven is 180 - 138 = 42º | ||||
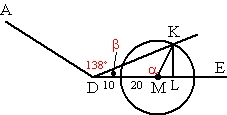
| d. | In driehoek MLK: cos(180 -
α) = ML/MK = ML/20 ML = 20 cos(180 - α) = -20cosα DL = DM + ML = 30 - 20cosα |
 |
|||
| e. | DL = 30 - 20cosα sin(180 - α) = KL/KM ⇒ KL = 20 sin(180 - α) = 20sinα tanβ = KL/DL = 20sinα/(30 - 20cosα) = 2sinα/(3 - 2cosα) |
||||
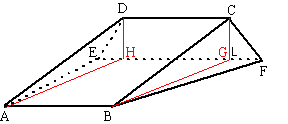
| 10. | a. | zie hiernaast. CG staat loodrecht op EF |
 |
||
| b. | tanα =
GC/GB ⇒ GB = GC/tanα
= 4/tanα prisma AHD.BGC heeft grondvlak BGC en hoogte AB BGC heeft oppervlakte 1/2 4/tanα 4 = 8/tanα De inhoud van het prisma is 8/tanα 10 = 80/tanα tanβ = GC/GF
⇒
GF = GC/tanβ
= 4/tanb |
||||
| De totale inhoud is
het prisma plus twee piramides: 80/tanα
+ 64/3tanαtanβ = 3 80tanβ/3tanαtanβ + 64/3tanβtanα de tellers optellen geeft de gevraagde formule. |
|||||
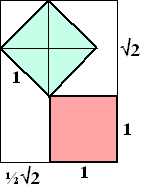
| 11. | a. | De
situatie is dan als hiernaast. De diagonaal van een vierkant met zijde 1 heeft lengte √2 De rechthoek er omheen heeft dan afmetingen 1 + √2 bij 0,5√2 + 1 De omtrek is (1 + √2)(0,5√2 +1) = 0,5√2 + 1 + 1 + √2 = 2 + 1,5√2 |
|
||
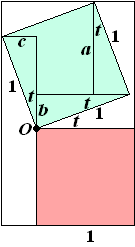
| b. | In de
figuur hiernaast zijn een aantal hulplijnen getrokken. Daardoor ontstaan drie kleine rechthoekige driehoekjes, waarin we SOS-CAS-TOA mogen toepassen. cos t = a/1 geeft a = cos t sin t = b/1 geeft b = sin t sin t = c/1 geeft c = sin t De hoogte van de rechthoek is 1 + a + b, de breedte is 1 + c De oppervlakte is dan; (1 + a + b)(1 + c) = (1 + cos t + sin t)(1 + sin t) En dat is precies de gezochte formule. |
|
|||
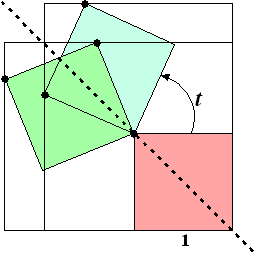
| c. | De figuur hiernaast
is op verschillende manieren te verkrijgen:
Spiegelen in de diagonaal van het vierkant. De lengte en breedte van de omschrijvende rechthoek verwisselen.
|
|
|||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||