© h.hofstede (h.hofstede@hogeland.nl)

Grafieken van exponentiële functies.
De exponentiële functies  y = B • gx kunnen we in twee soorten indelen:
soort I.  de groeifactor g is groter dan 1:

  TOENAME
soort II:  de groeifactor g zit tussen 0 en 1:

AFNAME
Natuurlijk zijn er nog een paar andere gevallen, maar die zullen we niet bekijken, dat zijn:
1. g = 1.   Da's nogal saai, want dan staat er y = B • 1x  ofwel  y = B.
De grafiek is een horizontale lijn op hoogte y = B.
2. g = 0.  Nog saaier:  y = B • 0x = 0  en dat is de x-as.
3.

g < 0. Hmmm... wel interessant eigenlijk, maar ook deze gevallen zullen we verder niet bekijken.
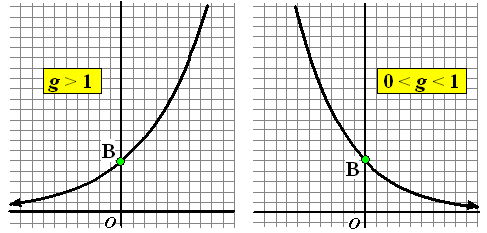
De grafieken van soort I en soort II hierboven zien er nogal verschillend uit. Dat is ook logisch als je bedenkt dat bij soort I de groeifactor g groter dan 1 is, dus zal de hoeveelheid toenemen. Bij soort II is g kleiner dan 1 en zal er sprake zijn van afname. Hier staan twee typische grafieken:

Er valt nog iets op aan deze grafieken.
Ze lijken nooit onder de x-as te komen.
Daar aan die zijkanten lijkt de x-as een horizontale asymptoot te zijn (dat is aangegeven met een pijl)
Dat dat inderdaad zo is kun je zo inzien:
• als 0 < g < 1 moet je aan de rechterkant kijken dus een heel groot positief getal voor x  nemen.
dan wordt  g10000... = g • g • g • g • g • g • g • g • g • g • g • g • g • g • g • g • g • g • g • g • .......
Dat wordt steeds kleiner, maar omdat g positief is kan hier nooit een negatief getal uitkomen.
• als g > 1  moet je aan de linkerkant kijken dus een heel groot negatief getal voor x nemen
Dan geldt  g -100000... =  1/g100000......  en als g100000.... heel groot wordt, dan wordt  1/g100000....  dus heel klein.
Maar weer nooit negatief!
1. Welke asymptoten hebben de grafieken van de volgende functies?
a. f(x) =  3 • 2x  c.    f(x) =  2 • 5x + 4
b. f(x) = 5 - 2 • 1,8x   d.  
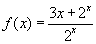2. Hieronder staan 3 grafieken van de vorm  y = B • gx 
Bepaal van elk van deze grafieken de waarden van  B  en g.

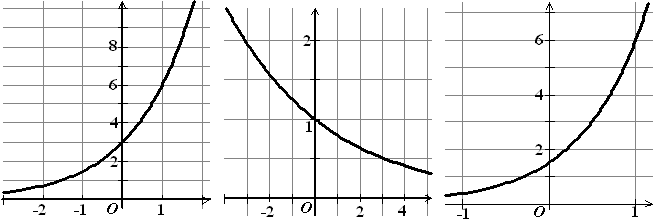
Laatste vraag:  Wie is de steilste?
Die kromme grafieken van exponentiële functies lijken wat op de kromme grafieken die we al eerder tegenkwamen bij parabolen, en x3  en x100  dergelijke functies. 

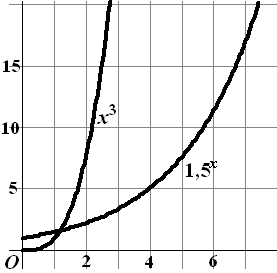
Hierboven zie je de grafieken van x3 en  1,5x . Het lijkt erop dat x3 veel steiler loopt dan 1,5x .
Maar dat blijkt niet zo te zijn!!!!!!
Bij grotere x zal de grafiek van 1,5x die van x3  toch weer "inhalen".
(om precies te zijn gebeurt dat bij x ongeveer 23,29 op hoogte ongeveer 12638, reken het zelf maar na).
En dat is geen toeval: dat gebeurt altijd! Op den duur wordt  gx  (g > 1)  altijd groter dan  xn
Dus zelfs  1,001x  zal het op den duur winnen van  x400  (dat duurt trouwens wel even..... bij x iets meer dan 6 miljoen!)
Conclusie:

gx   (g > 1) wordt op den duur  (voor grote x)  altijd groter dan xn
3. Gegeven zijn de functies  f(x) = 12 • x12   en  g(x) = 1,2 • 1,2x 
Bepaal met je rekenmachine voor welke x geldt dat  f(x) < g(x).
 

-0,81< x < 0,84
x > 408
4. Bepaal de snijpunten van de grafieken van y = x5  en  y = 5x

(1.76, 17.12)
   
5. Examenopgave HAVO Wiskunde A, 2022-I

In 2015 was het jaargemiddelde van de CO2-concentratie in de lucht 400,8 ppm (parts per million: het aantal CO2-deeltjes per miljoen luchtdeeltjes)
Wereldwijd worden er afspraken gemaakt met als doel de CO2-concentratie omlaag te brengen. Veronderstel dat het inderdaad lukt om de CO2-concentratie na 2015 zodanig te laten dalen dat het jaargemiddelde in 2050 nog maar 350 ppm is. Dan kan er bijvoorbeeld sprake zijn van afname volgens
- een lineair verband of
- een exponentieel verband.

In beide gevallen is het jaargemiddelde in 2015 gelijk en is ook het jaargemiddelde in 2050 gelijk. Echter, een CO2-concentratie van bijvoorbeeld 375 ppm wordt in het ene geval op een eerder moment bereikt dan in het andere geval.

Leg uit, zonder berekeningen te geven, in welk van de twee genoemde gevallen de CO2-concentratie het eerst de waarde 375 ppm bereikt.
   
 

© h.hofstede (h.hofstede@hogeland.nl)