|
|
 |
|
De ellips. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
Deze les gaan we de conflictlijn van een punt
F met een cirkel c bekijken, waarbij we dat punt F binnen
die cirkel kiezen.
We zoeken dus punten P waarvoor geldt dat de afstand tot punt F gelijk
is aan de afstand tot de cirkel c.
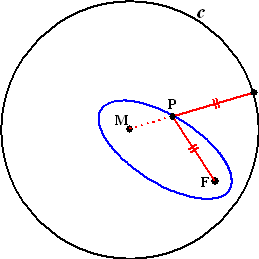
Dat ziet er ongeveer zo uit als hiernaast.
Die cirkel heet natuurlijk de richtcirkel.
Die punten P liggen allemaal op de blauwe kromme. Die kromme noemen we
een ellips.
Aan de stippellijn zie je dat de afstand van P tot de cirkel gelijk is
aan de straal van de cirkel (r) min de afstand van P tot
M.
Ofwel: d(P, c) = r - d(P,M) = d(P, F).
Daaruit volgt d(P,M) + d(P,F) = r |
 |
Maar wacht eens even....
Die ellips is een symmetrische figuur. Dus kun je spiegelen.....
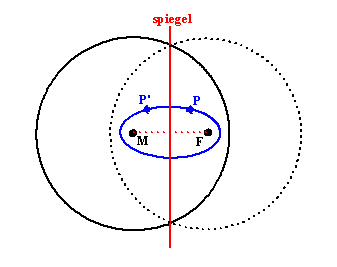
Hiernaast is de ellips horizontaal neergelegd. Daarin is te zien dat je,
als je een punt P van de ellips spiegelt in de lijn die midden tussen M
en F doorloopt, je wéér een punt P' van de ellips krijgt.
Dus onze blauwe ellips hiernaast is óók de verzameling van punten die
gelijke afstand hebben tot de gestippelde cirkel (met middelpunt F) en
punt M.
| |
| M speelt dezelfde rol als
F! |
|
| |
|
 |
De punten M en F noemen we de
brandpunten van de ellips (een brandpunt heet ook wel
focus).
We gaan nu die cirkel even weer vergeten en
spreken over een ellips af: |
|
|
|
Een ellips is de verzameling punten
waarvoor de totale afstand tot twee brandpunten constant is. |
|
|
|
En nu
een formule graag!
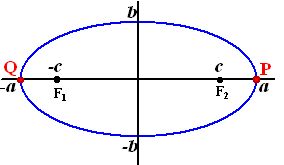
Laten we die twee brandpunten op
de x-as leggen in de punten (c,0) en
(-c, 0) zoals hiernaast getekend.
De ellips snijdt de x-as in a en -a en
de y-as in b en -b.
We weten intussen al dat de afstanden van een willekeurig punt van de
ellips tot F1 en F2 samen constant zijn.
Dat geldt dus ook voor punt P hiernaast.
Vanwege de symmetrie geldt PF1 + PF2 = PF1
+ F1Q = 2a
Dat betekent dat voor alle punten P van de ellips geldt:
|
 |
| |
|
|
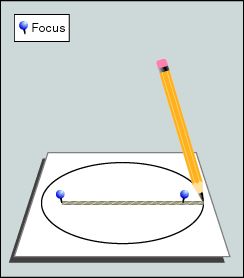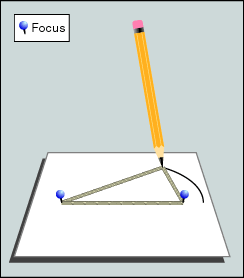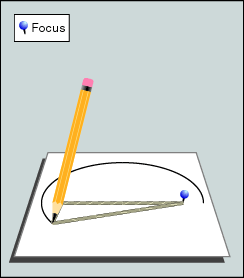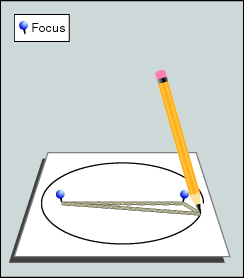 |
Deze eigenschap maakt het mogelijk om op
eenvoudige manier met twee punaises en een touwtje een ellips te
tekenen.
Steek de punaises in de brandpunten, leg het touwtje eromheen, trek het
strak, en tekenen maar! |
| |
|
Stel dat punt P = (x, y)
Omdat F1 = (-c, 0) en F2 = (c, 0)
geldt met Pythagoras dat: |
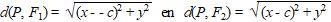
Samen moet dat gelijk zijn aan 2a:
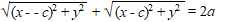 |
Uit deze vergelijking kun je een
veel mooiere vergelijking voor een ellips afleiden.
Dat mag je lekker zelf doen in de volgende opgave. |
|
|
|
|
|
|
| En daarmee hebben we de
vergelijking van een ellips gevonden... |
|
|
|
MAAR.... |
|
|
|
We hebben daarbij wel stiekem een
aanname gemaakt....
En die aanname zit hem in de tekening van de ellips.
Kijk maar eens wat er zou gebeuren als b > a:
dan kun je de Pythagoras van opgave 1c) helemaal niet gebruiken!
Wat is er dan aan de hand?
Dat kun je het best zien door b langzaam steeds groter te maken
(bij vaste a).
Als b groter wordt (bij gelijkblijvende a), dan wordt c
steeds kleiner, immers c2 = a2
- b2.
Dat betekent dat de brandpunten steeds dichter naar elkaar en naar de
oorsprong toe gaan.
Op het moment dat b = a geldt c = 0. Dat wil
zeggen dat beide brandpunten in de oorsprong liggen.
Dan is dus d(P,O) + d(P,O) = 2a ofwel
d(P,O) = a.
Het is een cirkel met straal a geworden!!!!!
Dat kun je ook eenvoudig aan de vergelijking van de ellips zien: als je
neemt b = a staat er x˛/a˛
+ y˛/a˛
= 1
dat is hetzelfde als x2 + y2 = a2
en die herkennen we uiteraard nog van "vroeger" als
een cirkel met straal a.
En als b groter dan a wordt, dan schuiven de brandpunten
over de y-as weer uit elkaar. In dat geval geldt c2
= b2 - a2 , en nu liggen de
brandpunten bij (0, c) en (0, -c).
Samengevat: |
|
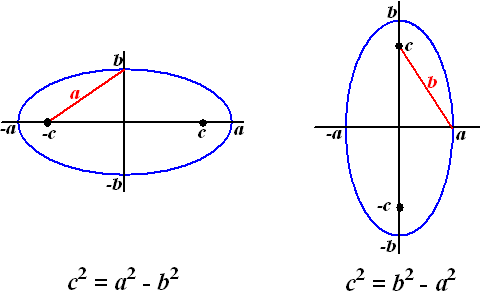 |
| |
|
| Natuurlijk hoeft het midden van de
ellips niet in de oorsprong te liggen. Je kunt hem verschuiven met de
(hopelijk) intussen bekende translaties: |
| |
|
|
vervang x door x
-
a ⇒ schuif de
grafiek a naar rechts
vervang y door y
- a
⇒ schuif de grafiek a
omhoog |
|
| |
|
En als je een formule van een
verschoven ellips krijgt dan kun je, net als bij de cirkel en parabool,
door kwadraat afsplitsen die translaties zichtbaar maken.
Voorbeeld.
Gegeven is de ellips 4x2 + 16x + 2y2
- 12y + 14 = 0.
Geef de coördinaten van de toppen en de brandpunten, en schets de
ellips.
oplossing:
4(x2 + 4x) + 2(y2
- 6y)
+ 14 = 0
4(x2 + 4x + 4 - 4) + 2(y2
- 6y
+ 9 - 9) + 14 = 0
4(x + 2)2 - 16 + 2(y
- 3)2 - 18 + 14
= 0
4(x + 2)2 + 2(y - 3)2 = 20 |
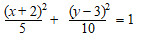 |
Dus a
= √5 en b =
√10. Omdat b > a lagen
de brandpunten (vóór de translaties) op de y-as.
c2 = b2 - a2 = 10
- 5 = 5 dus c = √5.
De brandpunten waren oorspronkelijk (0, ±√5)
en de toppen waren (0, ±√10)
en (±√5,
0)
maar de ellips is 2 naar links en 3 omhoog geschoven.
Dat geeft brandpunten (-2, 3 ±√5)
en toppen (-2, 3±√10)
en (-2±√5,
3) |
| |
|
|
En nu het gezonde boerenverstand... |
| |
|
Zo'n ellips is natuurlijk niets anders dan een
afgeplatte of uitgerekte cirkel. Dus kun je ook makkelijk de formule
ervan afleiden uit de formule van een cirkel.
Begin met een cirkel met middelpunt de oorsprong en straal 1. De
vergelijking daarvan is natuurlijk x2 + y2
= 1.
Als je nou de horizontale as van de ellips gelijk wilt maken aan 2a
dan moet je de cirkel vermenigvuldigenten opzichte van de y-as
met factor a. Dat doe je door in de vergelijking x te
vervangen door x/a
Daarna kun je op dezelfde manier de verticale as van -b
tot b krijgen door te vermenigvuldigen ten opzichte van de x-as
met factor b: vervang y door y/bDat
geeft dan automatisch de gezochte ellipsformule. |
 |
| |
|
|
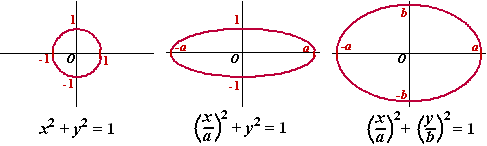 |
| |
|
| Omgekeerd is dit dan ook meteen
het bewijs dat die formule hoort bij een afgeplatte of uitgerekte
cirkel. Dat is precies de reden dat we in zoveel situaties ellipsen
tegenkomen. Eigenlijk elke keer als je schuin tegen een cirkel aankijkt
(of de schaduw van een cirkel ziet). |
| |
|
|
 |
| |
|
| 2. |
Schets de volgende ellipsen en geef coördinaten
van de brandpunten en de toppen. |
| |
|
|
|
| |
a. |
4y2 + 9x2
-
40y + 18x + 73 = 0 |
|
| |
b. |
4y2 + x2 +
16y - 4x + 19 = 0 |
|
| |
c. |
2y2 + x2 +
20y - 14 = 0 |
|
| |
d. |
9y2 + 64x2
-
144y - 384x + 576 = 0 |
|
| |
|
|
|
| 3. |
Een algemene vergelijking van een
ellips is ax2 + by2 +
cx + dy + e = 0
Hoe kun je aan zo'n algemene vergelijking direct zien of de
brandpunten op de x-as liggen of op de y-as? |
| |
|
|
|
| 4. |
Stel een vergelijking op van de
volgende ellipsen: |
| |
|
|
|
| |
a. |
Met de toppen (-8,0) en (8,0) en (0, -5)
en (0,5) |
| |
b. |
Met de toppen (0,0) en (4,0) en (2, -6) en
(2,6) |
| |
c. |
Met de toppen (1, -5) en (7,-5) en (4,-4)
en (4,-6) |
| |
d. |
Met de toppen (0, 6) en (0, -6) en de
brandpunten (-8,0) en (8,0) |
| |
e. |
Met de toppen (5,2) en (-5,2) en de
brandpunten (-3,2) en (3,2) |
| |
|
|
|
| 5. |
Een ellips heeft als richtcirkel
x2 + (y + 2)2 = 81 en als
één van de brandpunten (6, -2)
Geef een vergelijking van deze ellips |
| |
|
|
|
| 6. |
Een ellips heeft een brandpunt
(4,0) en een top (10,0).
Geef een formule. |
| |
|
|
|
| 7. |
Gegeven is de ellips:
x˛/6 +
y˛/9
= 1 |
| |
|
|
|
| |
a. |
Geef de coördinaten van de toppen
van deze ellips. |
| |
|
|
| |
b. |
Geef de vergelijking van de ellips
in de vorm ax2 + by2
= c. |
| |
|
|
| |
c. |
Bereken de coördinaten van de
snijpunten van de ellips met de lijn y = x +
1. Geef je antwoord in twee decimalen nauwkeurig. |
| |
|
|
|
(1.43, 2.43)
(-2.23, -1.23) |
|
| 8. |
Gegeven is de ellips: 4y2
+ x2 - 2x = 0 |
| |
|
|
|
| |
a. |
Een verticale lijn gaat door één
van de brandpunten van deze ellips, en staat loodrecht op de
lange as.
De lijn snijdt de ellips in de punten P en Q.
Bereken de lengte PQ. |
| |
|
|
| |
b. |
Bereken de coördinaten van de
snijpunten van deze ellips met de x-as |
| |
|
|
| |
c. |
Deze ellips snijdt van de lijn y
= x een lijnstuk af. Bereken de lengte van dat lijnstuk. |
| |
|
|
|
 |
|
| |
|
|
 |
|
| ©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
|
|
|