Egyptische breuken.

© h.hofstede (h.hofstede@hogeland.nl)

   

Hiernaast zie je een afbeelding van een gedeelte van de Rhynd-papyrus.
Het is het oudst bekende wiskundige geschrift op de wereld!
De Rhynd-papyrus werd in 1858 gevonden en komt uit ongeveer 1650 voor Christus!

Het is een enkele rol die een lengte heeft van maar liefst 5,4 meter en die 32 centimeter breed is. De rol bevat allerlei wiskundige begrippen, methoden en symbolen en 87 wiskundige problemen en hun oplossingen.

Het eerste deel van de papyrus bestaat uit de zogenaamde 2/n-tabel.
De breuken van de vorm 2/n (met oneven n) voor n = 3 tot en met n = 101 worden hier geschreven als  de som van zogenaamde eenheidsbreuken (ook wel stambreuken genoemd). Dat zijn breuken met teller 1.
Zo vind je er bijvoorbeeld dat  2/15 = 1/10 + 1/30.
Na de tabel volgen nog een groot aantal andere breuken die ook als som van zulke eenheidsbreuken worden geschreven.
Als wij tegenwoordig een breuk gaan schrijven als som van eenheidsbreuken, dan noemen we dat Egyptische breuken.
       
Waarom deden die gekke Egyptenaren dat?
       
Voor die gewone getallen gebruikten ze de volgende 7 symbolen
       

       
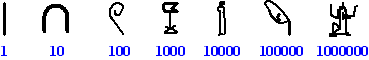Voor elk getal werd gewoon getekend "hoeveel je ervan nodig hebt". Daarbij schreven ze de grootste getallen links, en de kleinere rechts. Als het er teveel werden ook wel van boven (groot) naar onder (klein). Hiernaast zie je een paar voorbeelden.

De Egyptenaren kenden eigenlijk maar 3 symbolen voor breuken, namelijk voor 1/2, 2/3 en 3/4. Die zagen er zó uit:

   

       
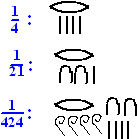
Alle andere breuken waren alleen maar eenheidsbreuken en die werden weergegeven door een dakje boven een gewoon getal te zetten (als het getal te groot was een dakje over het begin ervan) Hiernaast zie je een aantal Egyptische breuken.

Alle andere breuken moesten daarom wel geschreven worden als som van zulke eenheidsbreuken. Daarbij was verder nog de regel dat die eenheidsbreuken allemaal verschillend moesten zijn.
Dus 2/5 = 1/5 + 1/5 was fout.
Maar 2/5 = 1/3 + 1/15 is goed.

       
Hoe maak je van een gewone breuk Egyptische breuken?
       
Daar zijn een heleboel methodes (algoritmen) voor. We zullen er deze les een aantal bekijken.
       
Methode 1:   Haal steeds de kleinste eenheidsbreuk er af.   (ook wel het Fibonacci-algoritme)
       
Een voorbeeld zal denk ik wel duidelijk maken hoe het werkt.
Stel dat we de breuk 7/68 als Egyptische breuken willen schrijven.
⇒   10 • 7 is voor het eerst groter dan 68, dus de kleinste eenheidsbreuk is  7/70 (dat is 1/10)
⇒   Schrijf daarom 7/68 als  7/70 + x
⇒   Dan is x gelijk aan   7/68 - 7/70 = 1/340
⇒   Kortom:  7/68 = 1/10 + 1/340.

Het is niet altijd meteen in twee stappen klaar. Soms moet je met de nieuwe breuk die je krijgt dit proces gewoon nog een keer herhalen.

Voorbeeld:    7/8  =  7/14 + 3/8  =  1/2 + (3/9 + 1/24) = 1/2 + 1/3 + 1/24
       
1. Schrijf de volgende breuken als Egyptische breuken.
           
  a. 18/23
1/2+1/4+1/31+1/2852
d. 8/73

1/10+1/105+1/15330
  b. 6/17

1/3+1/51
e. 5/19

1/4+1/76
  c. 15/23

1/2+1/7+1/108+1/17388
f. 3/113

1/38+1/4294
           
       
Methode 2:  De Koppelmethode.
       
Schrijf eerst de breuk t/n  als t kopieën van 1/n. 
Dat mag natuurlijk niet, want die Egyptische breuken moeten allemaal verschillend zijn.
Maar nu gaan we die 1/n breuken twee aan twee samennemen.  Dat doen we met één van de twee volgende regels:
•  Als n even is, dan is 1/n + 1/n gelijk aan 2/n = 1/(0,5n)
•  Als n oneven is, dan is 1/n + 1/n = 2/(n + 1) + 2/(n(n + 1))  en die nieuwe  breuken zijn beiden met even noemer.

(Ga zelf maar na dat die tweede regel correct is).
Zo wordt het aantal breuken kleiner en verschillend.

Voorbeeld:   5/7 = 1/7 + 1/7 + 1/7 + 1/7 + 1/7 
=  2/8 + 2/56 + 2/8 + 2/56 + 1/7
= 1/4 + 1/4 + 1/28 + 1/28 + 1/7
= 2/4 + 2/28 + 1/7
= 1/2 + 1/14 + 1/7
Merk nog op dat onze eerste methode zou geven dat 5/7 = 1/2 + 1/5 + 1/70   
       
           
2. Schrijf de volgende breuken met de koppelmethode als Egyptische breuken.
             
  a. 4/17

1/5+ 1/45 + 1/77 + 1/11781
d. 3/11

1/6+1/11+1/66
  b. 5/22

1/5+1/66+1/22
e. 7/12

1/3+1/6+1/12
  c. 6/23

1/6+1/12+1/138+1/276
f. 9/27

1/4+1/27+1/28 + 1/95 + 1/17955
           
Methode 3:   De splitsmethode.

Die werkt het zelfde als de koppelmethode, maar nu gebruiken we voor oneven noemers de regel
 2/n = 1/n + 1/(n + 1) + 1/(n(n + 1))  . Deze methode is niet zo mooi, want geeft meer breuken, immers van twee breuken met oneven noemers laten we er eentje staan en de andere splitsen we in tweeën.

voorbeeld:
3/11 = 1/11 + 1/11 + 1/11
=  1/11 + 1/12 + 1/132 + 1/11
=  1/11 + 1/12 + 1/132 + 1/12 + 1/132
=  1/11 + 2/12 + 2/132
=  1/11 + 1/6 + 1/66 
       
Methode 4:  Met het tweetallig stelsel    
       
Noem de breuk weer t/n
Ga nu de teller vermenigvuldigen met een factor f:    1, 2, 4, 8, 16, 32, ....  enz. 
Doe dat net zolang totdat de rest van de deling kleiner is dan die factor f.
Stel dat dat voor het eerst gebeurt bij  t f /n = d rest r  (waarbij dan dus  r < f )
Dan kun je twee breuken opschrijven:  d/f  en  r/f 
Die d/f  en r/f  kun je eenvoudig schrijven als som van eenheidsbreuken (allemaal met noemers machten van 2).
De Egyptische breuk is nu gelijk aan   d/f  + 1/n · r/f

Voorbeeld.   Neem de breuk 12/19.
f = 1  geeft  12/19 = 0 rest 12  maar 12 is niet kleiner dan 1
f = 2 geeft   24/19 = 1 rest 5 maar 5 is niet kleiner dan 2
f = 4  geeft  48/19 = 2 rest 10 maar 10 is niet kleiner dan 4
f = 8  geeft  96/19 = 5 rest 1 en JAWEL:  1 is kleiner dan 8.
Dan is  d/f = 5/8  = 1/2 + 1/8  en  r/f  = 1/8
Dan is  12/19 = 1/2 + 1/8 + 1/19(1/8)  = 1/2 + 1/8 + 1/152
       
3. Schrijf de volgende breuken met behulp van het tweetallig stelsel als Egyptische breuken
             
  a. 6/13

1/4+1/8+1/16+1/52+1/208
d. 20/53

1/4+1/8 + 1/424
  b. 5/24

1/8+1/16 + 1/48
e. 10/49

1/8+1/16+1/98+1/196+1/784
  c. 3/17

1/4+1/8+ 1/34 + 1/68 + 1/136
f. 3/31

1/16+1/32 + 1/496 + 1/992
           
     

© h.hofstede (h.hofstede@hogeland.nl)