Lineaire recursievergelijkingen.

© h.hofstede (h.hofstede@hogeland.nl)
Een lineaire vergelijking is:   y = ax + b
Daarom is een lineaire recursievergelijking:   un = a • un - 1 + b

Neem als voorbeeld  un = 0,2un - 1 + 3  met  u0 = 4
Om een directe formule te maken voor un is het vaak handig gewoon eerst eens een aantal termen te gaan opschrijven. Misschien zien je wel een regelmaat.... je weet maar nooit.......

u0 = 4
u1 = 0,2 • u0 + 3
u2 = 0,2 • u1 + 3 = 0,2 • (0,2 • u0 + 3)  + 3  = 0,22 • u0 + 0,2 • 3 + 3
u3 = 0,2 • u2 + 3 = 0,2 • (0,22 • u0 + 0,2 • 3 + 3) + 3 = 0,23 • u0 + 0,22 • 3 + 0,2 • 3 + 3
u4 = 0,2 • u3 + 3 = 0,2 • (0,23 • u0 + 0,22 • 3 + 0,2 • 3 + 3) + 3 = 0,24 • u0 + 0,23 • 3 + 0,22 • 3 + 0,2 • 3 + 3
....

Voor un geeft dat het volgende:

Het laatste deel is een meetkundige rij, van achter naar voren geschreven. De reden is 0,2.
De som van een meetkundige rij kunnen we al berekenen. Voor deze rij geldt:

En daarmee wordt de formule voor de hele rij: 

   
Het dekpunt.

Het dekpunt van een recursievergelijking was de evenwichtswaarde E, weet je nog? Het was de x- of y-waarde van het punt waar in een webgrafiek de lijn y = x de lijn van de recursievergelijking snijdt.
Je kon die waarde vinden door op te lossen  un =  un - 1 = E.
Let wel: het was een mogelijke evenwichtwaarde. Of dat evenwicht bereikt werd of niet hing meestal af van de recursievergelijking en soms ook van de beginwaarde.

Lineaire recursievergelijkingen hebben hoogstens één dekpunt (immers twee rechte lijnen hebben hoogstens één snijpunt), en dat vind je als volgt: 
E = aE + b ⇒  E - aE = b  ⇒  E(1 - a) = b  ⇒  E = b/(1 - a)
 

un = a • un - 1 + b  heeft als evenwichtswaarde  E = b/(1 - a)
 
   
Handiger te onthouden.
   
Met die evenwichtswaarde is de directe formule voor un  veel eenvoudiger te schrijven, en dus eenvoudiger te onthouden.
Met de a = 0,2 en b = 3 van hierboven vind je:
Nou, daar staat dan weer een vrij eenvoudig te onthouden "woordformule":
   
un = evenwicht + an • (begin - evenwicht)
   
Convergeren en Divergeren.

Het feit of een rij van een lineaire recursievergelijking convergeert of divergeert hangt alleen af van a.
Hieronder zie je zes mogelijke gevallen.
   

   
Voor  a < -1  of  a > 1  is de rij  divergerend.
Voor  -1 < a < 1  is de rij convergerend.
Voor a = -1 is de rij alternerend.
Voor a = 1 is de rij rekenkundig.

(bij divergerend moet eigenlijk staan "i..h.a. divergerend", want als je begint met u0 = E dan divergeert de rij uiteraard niet).
   
   
  OPGAVEN
   
1. Een directe formule voor de rij met recursievergelijking   un = a • un-1 + b en beginterm u0 is:
   
 

       
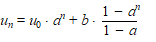  Leid deze directe formule af  
       
2. Stel een directe formule op die hoort bij de volgende recursievergelijkingen:
       
  a. un =  0,8 • un - 1 + 10  met  u0 = 100
       
  b. un = 2 • un - 1 - 10  met  u0 = 2000
       
3. Een vader opent voor zijn pasgeboren dochtertje op haar geboortedag een rekening met daarop €200,-
Elk jaar krijgt hij daarop 6% rente, en vervolgens stort hij er op haar verjaardag elk jaar €50,- bij.
Bereken algebraïsch hoeveel zijn dochtertje op haar 18e verjaardag op deze rekening zal hebben staan (nadat die €50 er bij is gestort)
     

€2116,15
       
4. Een boswachter krijgt een boswachterij onder zijn beheer waarin een enorm heideveld ligt. De man heeft wiskunde in zijn pakket gehad en besluit elk jaar nauwkeurig bij te houden hoeveel heideplantjes er in leven zijn. Tot zijn grote schrik merkt hij dat dat er steeds minder worden. De eerste vier metingen geven de volgende aantallen:
       
 
jaar 0 1 2 3
aantal 160000 128000 102400 81920
       
  a. Laat zien dat er sprake is van een exponentiële afname. Geef een recursievergelijking voor het aantal plantjes A(n). Geef ook een directe vergelijking en bereken wanneer er nog slechts 10000 plantjes over zullen zijn als dit zo doorgaat.
     

A(n) = 0,8A(n- 1)
A(n) = 160000• 0,8n
n = 13
  De man besluit elk jaar een vast aantal plantjes a te gaan bijplanten. Hij neemt voorlopig a = 24000. Neem aan dat los daarvan de exponentiële afname nog steeds doorgaat met dezelfde factor. Hij plant de nieuwe plantjes steeds aan het eind van het jaar dus die gaan nog niet dood. Zijn peildatum is steeds 1 januari.
       
  b. Laat zien dat hij bij een beginaantal van 81920 (zoveel zijn er nu) over 4 jaar dan 104402 plantjes zal meten.
Geef opnieuw een recursievergelijking en een directe vergelijking voor het aantal plantjes. Neem A(0) gelijk aan 81920.
       
  c. Bepaal op twee verschillende manieren hoeveel plantjes er met dit nieuwe systeem uiteindelijk zullen zijn.
     

120000
   
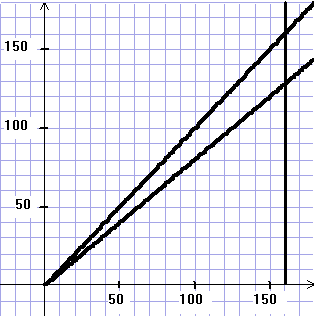
  De man wil uiteindelijk graag weer 160000 plantjes krijgen. Daarvoor zal hij het aantal a dus moeten vergroten.
In de figuur hieronder staat het begin van een webgrafiek. De lijn x = 160000 is ook aangegeven (de assen hebben een schaalverdeling in duizenden).
       
 

       
  d. Teken hierin de weblijnen voor de eerste drie jaren dat de man boswachter was.
Bepaal vervolgens met deze grafiek hoe groot de man a moet kiezen om uiteindelijk op 160000 plantjes uit te komen.
Teken tenslotte in deze figuur een nieuwe webgrafiek waarin je de volgende drie jaren weergeeft.
       
5. Een werkgever geeft zijn personeel elk jaar 300 vakantieuren. Verder heeft hij de regeling dat iedereen van de niet-opgenomen uren in een jaar 60% mee mag nemen naar het volgende jaar.
       
  Koos is in 1980 begonnen te werken bij deze werkgever. Hij neemt elk jaar 250 uren op.  Noem K(n) heet aantal vakantieuren dat Koos heeft in jaar n  (met n = 1 in 1980)
       
  a. Stel een recursievergelijking voor K(n)
     

Kn = 0,6Kn - 1 + 150
     
  b. Stel een directe vergelijking op voor K(n), en bepaal daarmee hoeveel vakantieuren Koos in 1990 heeft.
     

374,24 uur
     
  c. Hoeveel uur had Koos ongeveer per jaar moeten opnemen als hij in 1990 graag 400 uur zou hebben?
     

233
       
6. Voor een lineaire recursievergelijking geldt dat u0 = 100 en  u1 = 120.
Bereken in twee decimalen nauwkeurig u10 als je weet dat de evenwichtswaarde 600 is.
     

546,31
       
7. Twee dikke vriendinnen, Chrissie en Lotte, zijn letterlijk dikke vriendinnen. Ze besluiten een dieet te gaan volgen om af te vallen. Op werkdagen eten zij zo weinig dat ze in een week 2% van hun gewicht verliezen. Maar in het weekend mogen ze als beloning dan "vrij" eten  Dat betekent chips en taart en Macdonalds en dat betekent ook dat ze dan weer 3 kilo aankomen.

Als ze op maandagochtend beginnen weegt  Chrissie 120 kg en Lotte 130 kg.
 
 
       
  a. Stel een recursievergelijking op  voor het gewicht van de dames, en leg uit waarom dit "dieet" niet zal werken.
       
  b. Bereken met een directe formule hoeveel Lotte met dit dieet na 8 weken zal wegen.
     

132,98 kg
  Om echt af te vallen zullen de dames iets anders moeten proberen.
Lotte besluit tijdens de werkdagen nóg strenger te vasten zodat ze maar liefst 3% gewicht zal verliezen. In de weekeinden blijft ze gewoon 3 kilo aankomen.
Chrissie besluit tijdens de werkdagen de situatie gelijk te houden, maar in de weekeinden iets minder te eten zodat ze dan maar 2 kilo aankomt.

Als ze met dit nieuwe plan beginnen weegt Lotte 134 kg en Chrissie 126 kg.
       
  c. Na hoeveel weken van het "oude" dieet is dat?
     

11 weken
     
  d. Stel directe formules op voor het gewichten van de dames in de nieuwe situatie.
Bereken daarmee na hoeveel weken Lotte nog maar 3 kg zwaarder is dan Chrissie
     

13 weken
     
  Omdat hun gewichtsverschil steeds kleiner wordt denkt Lotte dat haar dieet effectiever is dan dat van Chrissie
     
  e. Leg uit dat dat op de lange duur niet zo zal zijn.
       
8. Een bomenkweker heeft nu een voorraad van 4000 bomen.
Elk jaar verkoopt hij 20% van zijn bomen, en daarna plant hij 300 nieuwe bomen. Het volgende jaar (t = 1) zal hij dus 3500 bomen hebben.
Neem aan dat het aantal bomen in zijn kwekerij geen geheel getal hoeft te zijn.
       
  a. Geef een recursievergelijking voor het aantal bomen bn   
       
  b. Geef een directe formule voor bn  en bereken wanneer er voor het eerst minder dan  1700 bomen zal hebben
     

n = 12
  c. Hoeveel bomen zal de kweker onder deze omstandigheden uiteindelijk hebben?
     

1500
  d. Hoeveel bomen (in plaats van 300) moet de kweker elk jaar bijplanten om uiteindelijk een bestand van 2000 bomen te hebben?
     

400
       
9. Bij een patiënt wordt een ader in zijn been afgesloten door een bloedprop. Om mogelijke fatale gevolgen tegen te gaan wordt een bloedverdunner, bijvoorbeeld Heparine, toegediend. Voor de patiënt geldt dat elke 6 uur na een injectie de helft van de Heparine weer uit het bloed verdwijnt is. Verder moet er minstens 2000 IE Heparine in het bloed aanwezig blijven  (IE = Internationale Eenheid)
We nemen aan dat de hoeveelheid Heparine in het bloed exponentieel afneemt.
H(t) is de hoeveelheid  Heparine in het bloed, t uur na het toedienen van de eerste injectie.
De eerste injectie bevatte 5000 IE Heparine, dus H(0) = 5000.
       
  a. Toon aan dat de hoeveelheid Heparine in het bloed elk uur met 11% afneemt.
       
  b. Bereken na hoeveel tijd een tweede injectie van 5000 IE Heparine moet worden gegeven. 
       
  Om te grote fluctuaties in de medicijnspiegel tegen te gaan wordt besloten om de patiënt elk heel uur een vervolginjectie van 300 IE Heparine te geven.
       
  c. Geef de recursievergelijking die bij dit proces hoort, en schets een stukje van de bijbehorende webgrafiek.
       
  d. Men wil de hoeveelheid van 300 IE omlaag brengen. Bereken de minimale hoeveelheid die nog gebruikt kan worden.
       
10. Gegeven is de recursieformule   un =  0,9 • un-1 + p • un-12 + 40

Neem eerst p = -0,04
       
  a. Bereken  u50 als u0 = 4  
       
  b. Teken hieronder een webgrafiek voor u0 tm u3  als u0 = 20. Teken in de figuur ernaast ook een tijdgrafiek
       
 
       
  Neem nu p = 0
       
  c. Geef een directe formule voor un  als u0 = 50
       
     

© h.hofstede (h.hofstede@hogeland.nl)