|
|||||
| 1. | de term,en zijn
achtereenvolgens: u0 u1 = au0 + b u2 = au1 + b = a(au0 + b) + b = a2u0 + ab + b u3 = au2 + b = a(a2u0 + ab + b) + b = a3u0 + a2b + ab + b ..... un = anu0 + an - 1b + an - 2b + .... + a2b + ab + b Dat blauwe is de som van een meetkundige rij, waarvan de reden a is en de volgende term anb De som daarvan is S = (anb - b) / (a - 1) = b (an - 1)/(a - 1) De hele som wordt dan S = anu0 + b (an - 1)/(a - 1) en dat is inderdaad de gegeven formule. |
||||
| 2. | a. | un = 0,8
un - 1 + 10 met u0
= 100 a = 0,8, b = 10, u0 = 100 dat geeft un = 100 0,8n + 10 (0,8^n - 1)/-0,2 = 100 0,8n + 5 (1 - 0,8n) |
|||
| b. | un = 2 un
- 1 - 10 met u0
= 2000 a = 2, b = -10, u0 = 2000 dat geeft un = 2000 2n - 10 (2^n - 1)/(2 - 1) = 2000 2n - 10 (2n - 1) |
||||
| 3. | u0
= 200 un = 1,06 un - 1 + 50 a = 1,06 en b = 50 Dat geeft un = 200 1,06n + 50 (1,06^n - 1)/(1,06 - 1) 18e verjaardag is u18 = 200 1,0618 + 50 (1,06^18 - 1)/0,06 = 2116,15 |
||||
| 4. | a. | De factoren zijn
achtereenvolgens 128000/160000 = 0,8
en 102400/128000 = 0,8 en
81920/102400 = 0,8 Dat is steeds gelijk en kleiner dan 1, dus er is sprake van exponentiλle afname. De recursievergelijking is un = 0,8 un - 1 met u0 = 160000 De directe vergelijking is A(n) = 160000 0,8n 10000 = 160000 0,8n 0,8n = 0,0625 n = log(0,0625)/log(0,8) = 12,4 Vanaf jaar nr. 13 zijn er minder dan 10000 plantjes. |
|||
| b. | An
= 0,8 An - 1 + 24000 met A0 =
81920 is de recursievergelijking nMin = 1 u(n) = 0,8 * u(n - 1) = 24000 u(nMin) = 81920 TABLE geeft dan nij n = 4 een aantal van 104402 De directe vergelijking is An = 81920 0,8n + 24000 (0,8n - 1)/(0,8 - 1) Dat is An = 81920 0,8n + 120000 (1 - 0,8n) A4 = 81920 0,84 + 120000 (1 - 0,84) = 104402 |
||||
| c. | Vul in de directe
formule van vraag b) voor n een oneindig groot getal in. Dan wordt 0,8n gelijk aan nul. Dan staat er A = 120000 Evenwicht: E = 0,8E + 24000 0,2E = 24000 E = 120000 |
||||
| d. |
 |
||||
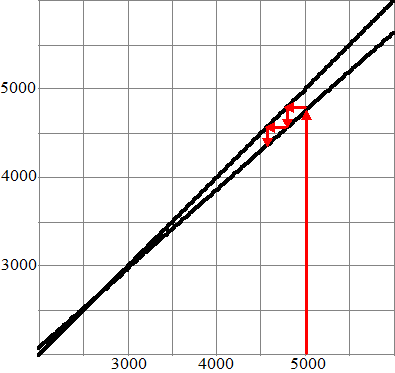
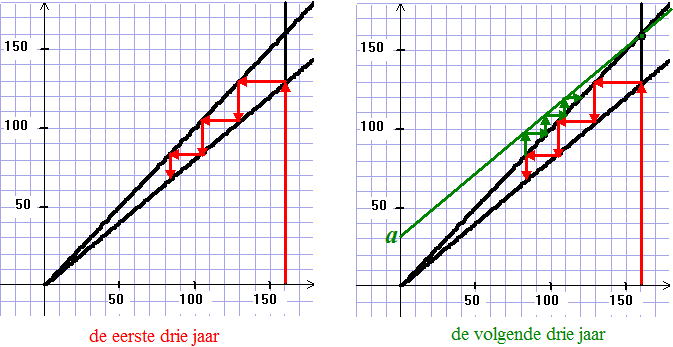
| In de rechterfiguur
is de lijn y = 0,8x omhooggeschoven totdat hij de lijn
y = x bij x = 160000 snijdt Dat geeft de groene lijn. a staat op de y - as en is iets meer dan 30000 |
|||||
| 5. | a. | K0 = 300 K1 = 300 + 0,6 (300 - 250) = 330 K2 = 300 + 0,6 (330 - 250) = 378 K3 = 300 + 0,6 (378 - 250) = 376,8 Kn = 300 + 0,6 (Kn - 1 - 250) Kn = 300 + 0,6 Kn - 1 - 0,6 250 Kn = 150 + 0,6Kn - 1 met K1 = 300 |
|||
| b. | 300 = 150 +
0,6u0 geeft u0 = 250
a = 0,6 en b = 150 Dat geeft de directe formule: Kn = 250 0,6n + 150 (0,6^n - 1)/(0,6 - 1) Kn = 250 0,6n + 375 (1 - 0,6n) 1990 is n = 11, en dat geeft K11 = 250 0,611 + 375 (1 - 0,611) = 374,55 |
||||
| c. | Als Koos x
uren opneemt ipv 250 dan wordt de recursievergelijking Kn
= 300 + 0,6 (Kn - 1 - x) Kn = 300 - 0,6x + 0,6Kn - 1 a = 0,6 en b = 300 - 0,6x Noem de eerste u0, dan is de directe vergelijking Kn = 300 0,6n + (300 - 0,6x) (0,6n - 1)/(0,6 - 1) Kn = 300 0,6n + 2,5 (300 - 0,6x) (1 - 0,6n) 1990 is dan n = 10 400 = 300 0,610 + 2,5 (300 - 0,6x) (1 - 0,610) 400 = 1,8139 + (300 - 0,6x) 2,485 160,24 = 300 - 0,6x 0,6x = 139,76 x ≈ 233 |
||||
| 6. | u0
= 100 en u1 = 120 dus 120 = a 100
+ b De evenwichtswaarde is 600 = b/(1 - a) dus 600(1 - a) = b en dat kun je invullen in de vorige vergelijking: 120 = 100a + 600 - 600a 500a = 480 a = 0,96 en dan is b = 600 (1 - 0,96) = 24 Met de handigere formule geeft dat: un = 600 + 0,96n (24 - 600) = 600 - 576 0,96n u1 = 600 - 576 0,9610 = 217 |
||||
| 7. | a. | un =
0,98un - 1 + 3 met u0
= 120 of 130. De evenwichtswaarde is: E = 0,98E + 3 en dat geeft E = 150. Ze zullen uiteindelijk meer wegen dan nu!! |
|||
| b. | E - 150 geeft met de
snelle formule: un = 150 + 0,98n
(130 - 150) u8 = 150 + 0,988 -20 = 132,98 kg. |
||||
| c. | Lotte: 134 =
150 + 0,98n (130 - 150). Die kun je met intersect van je GR oplossen, maar als je logaritmen kient kan het ook algebraοsch: -16 = -20 0,98n 098n = 0,8 n = log(0,8)/log(0,98) = 11 weken. |
||||
| d. | Lotte: un
= 0,97un - 1 + 3 met u0
= 134 Dat geeft un = 134 0,97n + 3 (0,97^n - 1)/(0,97 - 1) un = 134 0,97n + 100 (1 - 0,97n) Chrissie: un = 0,98un - 1 + 2 met u0 = 126 Dat geeft un = 126 0,98n + 2 (0,98^n - 1)/(0,98 - 1) un = 126 0,98n + 100 (1 - 0,98n) Lotte is 3 kg zwaarder dan Chrissie: Y1 = 134 0,97^X + 100 *(1 - 0,97^X) Y2 = 126 0,98^X + 100 * (1 - 0,98^X) + 3 Intersect geeft X = 12,6 weken |
||||
| e. | evenwicht voor Lotte:
E = 0,97E + 3 geeft E = 100 evenwicht voor Chrissie: E = 0,98E + 2 geeft E = 100 Uiteindelijk zullen ze het zelfde gewicht van 100 kg bereiken. |
||||
| 8. | a. | bn = 0,8bn - 1 + 300 met b0 = 4000 | |||
| b. | a = 0,8 en
b = 300 en u0 = 4000 bn = 4000 0,8n + 300 (0,8^n - 1)/(0,8 - 1) bn = 4000 0,8n + 1500 (1 - 0,8n) 1700 = 4000 0,8n + 1500 (1 - 0,8n) 1700 = 4000 0,8n + 1500 - 1500 0,8n 200 = 2500 0,8n 0,08 = 0,8n n = log(0,08)/log(0,8) = 11,3 Dus na 12 jaar zal hij voor het eerst minder dan 1700 bomen hebben. |
||||
| c. | E = 0,8E + 300 0,2E = 300 E = 300/0,2 = 1500 bomen. |
||||
| d. | E = 0,8E + b 0,2E = b 0,2 2000 = 400 = b dus hij moet dan elk jaar 400 bomen bijplanten. |
||||
| 9. | a. | In 6 uur verdwijnt de helft. Als de factor per uur gelijk is aan g dan geldt dus g6 = 0,5 Dat geeft g = 0,51/6 = 0,89 Als 89% overblijft dan verdwijnt 11% |
|||
| b. | De formule voor de
hoeveelheid in het bloed is H = 5000 0,89t
met t het aantal uren. 2000 = 5000 0,89t 0,4 = 0,89t t = log(0,4)/log(0,89) = 7,86 uur |
||||
| c. | Hn = 0,89 Hn
- 1 + 300 Hieronder staan de lijnen y = x en y = 0,89x + 300 |
||||
|
|
|||||
| d. | Wanneer ligt het
evenwicht op 2000? E = 0,89E + b 2000 = 0,89 2000 + b b = 220 Een dosis van 220 g per uur bijspuiten is genoeg. |
||||
| 10. | a. | mode seq nMin = 0 u(n) = 0,9 u(n - 1) - 0,04 u(n - 1)^2 + 40 u(nMin) = 4 TABLE geeft bij n = 50 dat u50 = 12,77 |
|||
| b. |
|
||||
| c. |
un = 0,9
un-1
+ 40 met u0 = 50 a = 0,9 en b = 40 Dat geeft un = 50 0,9n + 40 (0,9^n - 1)/(0,9 - 1) un = 50 0,9n + 400 (1 - 0,9n ) un = 400 - 350 0,9n |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||