|
|
 |
|
Dingen bij elkaar optellen.... |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
Het gaat er natuurlijk niet om
gewoon dingen bij elkaar op te tellen, maar om oneindig veel dingen
(meestal functiewaarden) op te tellen die steeds van grootte veranderen.
Dat klinkt nogal vaag, maar een voorbeeld zal waarschijnlijk een boel
duidelijk maken.
In het examen wiskunde B1 van 2004 tijdvak 2 stond de volgende opgave. |
| |
|
In een zeker gebied wordt
een grote toename van de bevolking voorzien. Om de daarmee
gepaard gaande problemen het hoofd te kunnen bieden, heeft
men een schatting nodig van de grootte van de bevolking voor
de komende jaren. Daarvoor stelt men het volgende model op
voor de grootte van de bevolking: B(t) = 228 e0,1t
Hierin is B het aantal mensen in duizenden en t
de tijd in jaren.
Het komende jaar loopt van t = 0 tot t = 1. In
deze opgave werken we met jaren van 360 dagen en maanden van
30 dagen.
(....)
Voedseldeskundigen hanteren
als vuistregel: per persoon is er per dag
0,4 kg vast voedsel nodig.
De totale benodigde hoeveelheid vast voedsel voor de inwoners van
het gebied in het komende jaar noemen we V (in kg).
Iemand wil berekenen hoe groot V is.
(....) |
|
| |
Stel eerst een formule op voor de
jaarbehoefte op tijdstip t:
V(t) = B(t) 0,4 1000 360 = 32832000 e0,1t
waarbij t in jaren is.
We willen nu graag het voedsel van dag 1 plus dat van dag 2
plus.....plus dat van dag 360 uitrekenen, en die dingen allemaal bij
elkaar optellen. Die voedselhoeveelheden variλren omdat de
bevolkingsgrootte varieert.
We willen dus optellen: V(0/360)
1/360 + V(1/360)
1/360 + ... + V(359/360)
1/360
Dat kan in ιιn keer met een integraal. Denk aan de Riemann sommen van
ooit...
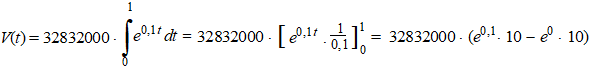
Dat is gelijk aan 32832000 1,0517 = 34529716 kg voedsel. |
| |
|
| Als je een serie functiewaarden optelt die
dicht bij elkaar liggen dan geldt: |
|
| |
|
|
|
| |
Nog een
keer hetzelfde voorbeeld.....
Het voorbeeld hierboven kan natuurlijk ook opgelost worden door de
voedselbehoefte per dag te bekijken, in plaats van per jaar.
Dan geldt: B(d) = 228 e0,1d/360
met d het dagnummer.
Het voedsel op elke dag optellen geeft dan:
V = 0,4 1000 (228 e0,1 1/360 + 228
e0,1 2/360 + ... + 228
e 0,1 360/360)
En al die dingen optellen geeft weer een integraal: |
| |
|
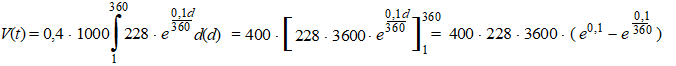 |
= 328320000 0,10489 = 34438503
Gelukkig ongeveer hetzelfde antwoord. Het verschil zit hem in die ene
dag verschil (d = 0 is nu niet meegeteld). |
| |
|
|
OPGAVEN |
|
|
| 1. |
Examenvraagstuk VWO Wiskunde B,
2004-1
Een nieuw industrieterrein grenst aan een
recht kanaal en heeft de vorm van een rechthoek OABC.
OA = 400 m en OC = 200 m. Zie de figuur hiernaast.
De grondprijs is afhankelijk van de afstand tot het kanaal: hoe
dichter bij het kanaal, hoe duurder de grond.
Het verband tussen de grondprijs P (in euro per m2) en de
afstand tot het kanaal x (in meters) wordt gegeven door de
formule P(x) = 100 0,998x
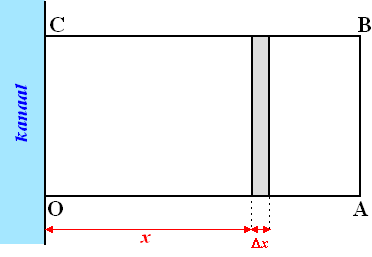
De totale grondprijs van het terrein is
te bepalen door rechthoek OABC in
rechthoekjes met lengte 200 meter en breedte Dx
meter te verdelen.
|
 |
| |
In de figuur is ιιn zo'n rechthoekje
getekend op x
meter van het kanaal. De totale grondprijs is dan bij benadering de som
van de grondprijzen van deze rechthoekjes. Bereken de totale
grondprijs met behulp van een integraal. |
| |
|
|
|
| |
|
|
|
| 2. |
Op een Petrischaal in een
laboratorium bevindt zich een bacteriekolonie. De schaal is
luchtdicht afgesloten en bevat 100 ml zuurstof. Het aantal
bacteriλn (N) wordt steeds groter. Er geldt N(t) = 100
e0,04t met t de tijd in uren.
Elke bacterie verbruikt per uur 0,06
ml zuurstof (6 10-5
ml).
De hoeveelheid zuurstof die de hele kolonie tussen t en
t + dt verbruikt (in ml) is dan gelijk aan 6 e0,04t
dt
Bereken hoe lang het duurt voordat de hele zuurstofvoorraad
van de schaal verbruikt is. |
| |
|
|
|
| |
|
|
|
| 3. |
Gegeven is de volgende meetkundige
reeks: 100 - 110 - 121 - 133,1 - 146,41 - 161,051 -
.....
We willen graag de som van de eerste 50 termen van deze reeks
bepalen. |
| |
| |
|
|
| a. |
Bepaal deze som met een formule voor de
som van een meetkundige reeks. |
|
| b. |
Benader deze som met een integraal. |
|
| |
|
|
|
| |
|
|
| 4. |
 |
| |
|
|
| |
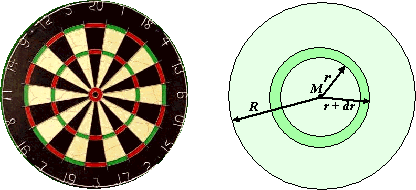
Iemand gooit een pijltje
op een dartboard met straal R.
Het pijltje komt op een willekeurige plek van het bord terecht.
Je kunt zo'n dartbord beschouwen als stroken met dikte dr.
De kans dat het pijltje in zo'n strook terechtkomt is dan
evenredig met de oppervlakte ervan.
De gemiddelde afstand van
het pijltje tot het middelpunt is de verwachtingswaarde van alle
afstanden.
Wat is de gemiddelde afstand van het pijltje tot het middelpunt
van het bord? |
| |
|
|
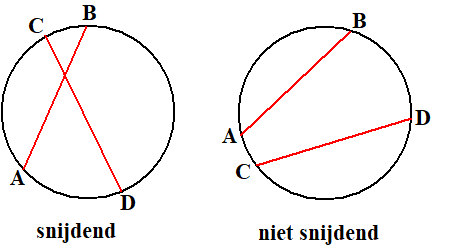
| 5. |
Teken in een cirkel
willekeurig twee koorden AB en CD
Hoe groot is de kans dat die elkaar snijden? |
| |
|
|
|
| |
 |
| |
|
|
|
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|
|
|