| |
 |
|
Differentieerbaarheid. |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
Deze les gaan we bekijken wat het
betekent als de afgeleide functie f ' van een functie f
continu is.
Volgens de simpelste afspraak van continuďteit betekent dat, dat je
de grafiek van f ' kunt tekenen zonder je potlood van het
papier te halen. En volgens de "officiële" afspraak betekent het dat
voor x = a geldt: |
|
|
|
|
|
| |
|
|
|
Daarin staan die
eerste twee er alleen maar om er voor te zorgen dat de derde bestaat.
Maar wat betekent het nou voor
f zélf?
|
Als f '
continu is, dan betekent dat, dat de grafiek van f ' geen vreemde
sprongen vertoont.
Maar f ' stelt de helling van f voor.
Dus dat betekent dat de helling van f geen vreemde sprongen
vertoont.
De helling van f mag dus best veranderen maar dan wel
gelijkmatig, niet ineens heel abrupt.
Een hele abrupte verandering in de helling zou je in de grafiek zien als
een "knik", immers dan verandert de helling ineens van de ene waarde
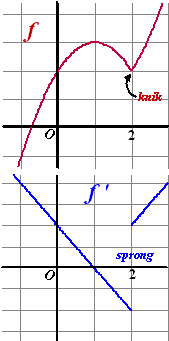
naar de andere. Hiernaast zie je onder elkaar de grafiek van zo'n f
met de bijbehorende f ' (Het is de trouwens
de grafiek van
f(x) = x│x
- 2│+ 2 maar dat doet er even niet toe)
Je ziet dat bij x = 2 de grafiek van f ' een
sprong vertoont (dus niet continu is). De grafiek springt van -2
naar 2. Dat zie je in de grafiek van f terug als een knik.
Aan de linkerkant van die knik is de helling immers gelijk aan -2,
en aan de rechterkant gelijk aan 2.
Als de afgeleide f' van een functie f continu is,
dan noemen we deze functie f zélf
differentieerbaar.
Manieren om
niet-differentieerbaar te zijn. |
 |
| |
|
|
|
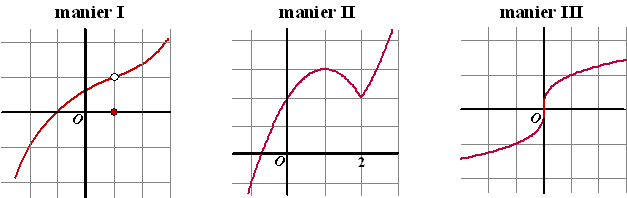
| Er zijn eigenlijk
drie basis-manieren waarop een functie f niet-differentieerbaar
kan zijn, en dat zijn de volgende: manier I:
De functie f zelf is niet continu.
Kijk, als de functie f niet continu is bij x = a ,
dan kun je het ook niet hebben over de helling in dat punt. Die hebben
we ooit immers gedefinieerd als de helling tussen dat punt en een
"punt-vlak-ernaast". Nou, als de functie niet continu, dan is dat "punt-vlak-ernaast"
er niet! In dit geval bestaat de helling f '(a)
uiteraard ook niet.
manier II. f is wél continu, maar
f ' vertoont een sprong.
Dat is het geval hierboven: f heeft een knik.
manier III: f is wél continu, maar f
' heeft een verticale asymptoot.
Dat betekent dat de grafiek van f dus wel gewoon te tekenen is,
maar dat de helling in x = a oneindig groot wordt. Dat is
zo als de raaklijn in x = a verticaal is! Dan bestaat
f´ niet, en dus kan hij ook niet continu zijn.
Hieronder zie je bij alle drie de manieren een voorbeeld. |
| |
|
|
|
|
 |
| |
|
|
|
| Manier I kan
natuurlijk op veel meer manieren gebeuren, bijvoorbeeld door een functie
met een verticale asymptoot, of een enkele sprong ergens. Grafiek III
heeft in de oorsprong een verticale raaklijn, dus bestaat daar de
helling f ' niet. Een bekend voorbeeld van zo'n
functie is bijvoorbeeld y = 3√x.
Je ziet verder dat de functies in II en III wél overal continu zijn,
maar dus niet differentieerbaar. |
| |
|
|
|
| |
|
|
|
|
|
|
| 1. |
Onderzoek of de volgende functies
differentieerbaar zijn op hun hele domein. |
| |
|
|
|
|
|
|
| |
a. |
f(x) =
│2x + 6│ |
|
| |
|
|
|
|
|
|
| |
b. |
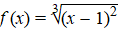 |
|
| |
|
|
|
|
|
|
| |
c. |
 |
|
| |
|
|
|
|
|
|
| |
d. |
 |
|
| |
|
|
|
|
|
|
| 2. |
Gegeven zijn de functies fa,b
door: |
| |
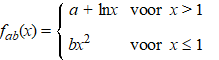 |
| |
|
|
|
|
|
|
| |
Onderzoek voor welke a en
b deze functies differentieerbaar zijn op hun domein. |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 3. |
Gegeven zijn de functies fa,b
door: |
| |
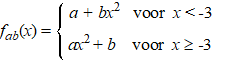 |
| |
|
|
|
|
|
|
| |
Toon aan dat er oneindig veel
waarden voor a en b zijn te vinden waarvoor deze
functies differentieerbaar zijn op hun domein. |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 4. |
Gegeven zijn de functies fa,b
door: |
| |
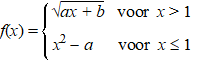 |
| |
|
|
|
|
|
|
| |
Onderzoek voor welke a en
b deze functies differentieerbaar zijn op hun domein. |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 5. |
Gegeven is de volgende functie f: |
| |
|
|
|
|
|
|
| |
 |
| |
|
|
|
|
|
|
| |
Bereken a en b als
deze functie differentieerbaar is in de punten x = 4 en
x = -4. |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 6. |
examenvraagstuk VWO
Wiskunde B, 1988 Gegeven is de op
〈-3,
π〉
differentieerbare functie: |
| |
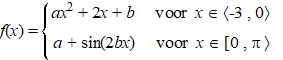 |
| |
|
|
|
|
|
|
| |
Bewijs dat a
= b = 1 |
| |
|
|
|
|
|
|
| 7. |
examenvraagstuk VWO
Wiskunde B, 1989. Gegeven is op R
de continue functie: |
| |
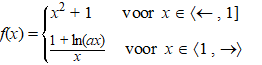 |
| |
|
|
|
|
|
|
| |
Ten opzichte van
een rechthoekig assenstelsel Oxy is F de grafiek van f. |
| |
|
|
|
|
|
|
| |
a. |
Bewijs dat a
= e. |
| |
|
|
|
|
|
|
| |
b. |
Bewijs ook dat f
niet differentieerbaar is in x = 1. |
| |
|
|
|
|
|
|
| 8. |
examenvraagstuk VWO
Wiskunde B, 1991. Van R naar R is
gegeven de functie: |
| |
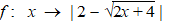 |
| |
|
|
|
|
|
|
| |
Toon aan dat f
niet differentieerbaar is in x = 0. |
| |
|
|
|
|
|
|
| 9. |
examenopgave VWO, 1971
Gegeven zijn de functies f(x) = x3
- 4x en g(x) = 2 - x
Verder is gegeven een functie hp
door:
hp(x) = f(x) als
x ≥ p
hp(x) = g(x) als
x < p |
| |
|
|
|
|
|
|
| |
a. |
Voor welke p is hp
continu? |
| |
|
|
|
|
|
|
| |
b. |
Voor welke p is hp
overal differentieerbaar? |
| |
|
|
|
|
|
|
|
| |
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|
|
 |
| |
|
|
|