|
|
 |
|
De correlatiecoŽfficiŽnt r. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
| Voor de covariantie
Cov(x, y) =
σxy
vonden we de volgende formule: |
| |
|
|
|
| |
|
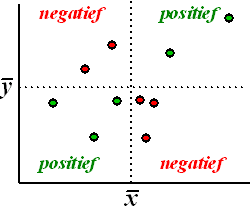
Het blijkt dat deze covariantie aardig
aangeeft hoe "goed" de punten op een lijn liggen. Dat kun je al een
beetje inzien door de figuur hiernaast te bekijken.
Voor de rode punten is de covariantie negatief, omdat
Δxi en
Δyi en tegengesteld teken
hebben, voor de groene punten is de covariantie positief want daar
hebben
Δxi en
Δyi het zelfde teken
(rechtsboven beiden positief, linksonder beiden negatief) .
Dat betekent dat de punten van een zelfde kleur elkaar "versterken" in
de covariantie. Veel rode punten zal een grote negatieve covariantie
geven, en veel groene punten een grote positieve covariantie.
Maar veel punten van een zelfde kleur betekent ook een grote correlatie!
Immers dan ligt de puntenwolk grotendeels "dezelfde kant op". Rode
punten geeft een negatieve r, groene punten een positieve. |
 |
| Het lijkt erop dat de
correlatiecoŽfficiŽnt en de covariantie zo ongeveer hetzelfde
doen....... |
| |
|
|
Zullen we voor
r
dan maar gewoon Cov(x,y)
nemen? |
| |
|
Dat zou kunnen, maar dat heeft
ťťn levensgroot nadeel.
En dat komt door de schaal.
Kijk, stel dat we bijvoorbeeld de lengte en het gewicht van mensen
hebben gemeten en daarvan een prachtige puntenwolk hebben gemaakt. Op de
x-as staat bijvoorbeeld de lengte in cm en op de y-as het
gewicht in kg. We hebben zelfs de covariantie bij deze puntenwolk
uitgerekend...
Maar als onze buurvrouw met precies dezelfde gegevens de lengte niet in
centimeters maar in meters op de x-as zet, dan krijgt zij
natuurlijk precies dezelfde puntenwolk, maar al haar
Δxi zijn 100 keer zo klein,
dus ook haar covariantie!
Dat kŠn natuurlijk niet!
Bij dezelfde vorm van de puntenwolk moet dezelfde r horen. Dit probleem
is te voorkomen door de covariantie te delen door de breedte van de x-waarden.
En daarvoor nemen we.....juist!....uiteraard!!....de standaarddeviatie
σx natuurlijk!!!
Dan veranderen we eigenlijk alle
Δxi
van een absolute afstand naar hoeveelste deel van de x-breedte
het is. Dan is dat niet meer van de schaal afhankelijk.
En voor de y-schaal geldt natuurlijk precies hetzelfde.
Daarom delen we de covariantie ůůk door
σy.
HŤ hŤ, dat geeft dan eindelijk een goede waarde voor r: |
| |
|
|
|
| |
|
Daarmee hebben we natuurlijk nog
niet verklaard waarom bij een perfecte rechte lijn r = 1 of r
= -1 zal
horen. Of zelfs niet waarom bij een rechte lijn r maximaal zal
zijn......
In de verdieping hiernaast laten we daar een voorbeeld van zien, en
zelfs een soort van "bewijs"...... |
| |
 |
| |
|
|
OPGAVEN |
| |
|
| 1. |
Bereken de correlatiecoŽfficiŽnt van de volgende
gegevens: |
| |
|
|
|
| |
| x |
1 |
2 |
3 |
3 |
5 |
6 |
| y |
7 |
5 |
3 |
6 |
5 |
3 |
|
| |
|
|
|
| |
|
|
|
| 2. |
De volgende tabel geeft voor zeven dagen de
hoogst gemeten temperatuur (T in ļC) op die dag en het aantal
uren (u) zon. |
| |
|
|
|
| |
| T (in ļC) |
16 |
17 |
17 |
18 |
19 |
20 |
22 |
| u (in uren) |
9 |
10 |
11 |
10 |
12 |
11 |
13 |
|
| |
|
|
|
| |
a. |
Bereken de correlatiecoŽfficiŽnt van
deze gegevens. |
| |
|
|
|
| |
b. |
Je kunt de temperatuur ook
uitdrukken in graden Fahrenheit. Daarvoor geldt: F = C ē 1,8 +
32
Verander de temperaturen naar graden Fahrenheit, en laat zien
dat r hetzelfde blijft. |
| |
|
|
|
| 3. |
Stel dat je een hele serie meetgegevens hebt met
een bepaalde gemiddelde x en y.
Hoe verandert r dan als je er een punt aan toevoegt, dat
precies ligt op die gemiddelde x en y?
Bewijs je antwoord met behulp van de formule voor r. |
| |
|
|
|
| |
|
|
|
| 4. |
Leg met behulp van de formule voor r uit,
dat de correlatiecoŽfficiŽnt voor een serie punten die precies
op een horizontale lijn liggen niet bestaat.
Kun je uitleggen waarom men in dit geval kiest voor r =
0? |
| |
|
|
|
| |
|
|
|
| 5. |
Hieronder staat een tabel van drie
meetgegevens. De laatste y-waarde is voorlopig onbekend,
en is p genoemd. |
| |
|
|
|
| |
|
| |
|
|
|
| |
Voor de correlatiecoŽfficiŽnt geldt
dan: |
| |
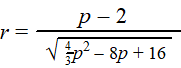 |
| |
|
|
|
| |
a. |
Toon dat aan. |
| |
|
|
|
| |
b. |
Bereken de extreme waarde van de
functie r(p) en leg daarna uit waarom je dit
resultaat inderdaad had kunnen verwachten. |
| |
|
|
|
| |
|
|
|
| 6. |
De formule voor de centrale lijn die
we eerder vonden ging ervan uit dat x oorzaak was, en
y gevolg.
De formule voor r is niet afhankelijk van wat oorzaak of wat
gevolg is.
Hoe kun je zonder berekeningen dat direct aan deze formule zien? |
| |
|
|
|
| |
|
|
|
|
|
Een verband tussen r en a. |
| |
|
| Als je de twee formules voor r
(de correlatiecoŽfficiŽnt) en a (de helling van de regressielijn)
met elkaar vergelijkt dan lijken die nogal op elkaar: |
| |
|
|
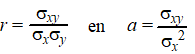 |
| |
|
| Daaruit kun je vrij eenvoudig
concluderen (bewijs het zelf maar) dat: |
| |
|
|
|
| |
|
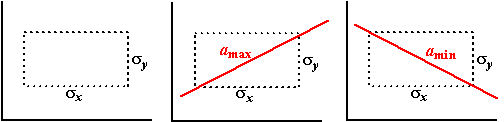
Dat lijkt misschien een beetje
een vreemd resultaat. De helling van de beste lijn (a)
hangt af van hoe goed de punten op een lijn liggen (r)???
Toch is dat wel logisch als je het volgende bedenkt.....
Die σy/σx
is de helling van de centrale lijn. Die
bepaalt de globale afmetingen van de puntenwolk. Immers
σy zegt hoe ver de x-waarden
uit elkaar liggen (dus hoe breed de puntenwolk is) en
σy hoe ver de y-waarden
uit elkaar liggen (dus hoe hoog de puntenwolk is). Samen bepaalt dat de
"buitenomtrek van de puntenwolk" . Een soort van rechthoek waar de
puntenwolk grotendeels in ligt: |
| |
|
|
 |
| |
|
Als je weet dat de punten van je
puntenwolk op de linker- rechter- boven- ťn onderrand van de rechthoek
moeten liggen, zie je hierboven de maximaal haalbare waarde voor a
en ook de minimaal haalbare a.
De r bepaalt vervolgens in hoeverre deze maximale of minimale waarden
ook werkelijk bereikt worden. Eigenlijk "hoeveelste deel van de a
gehaald wordt". |
| |
|
| |
|
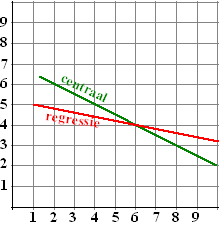
| 7. |
Hiernaast zie je voor een
puntenwolk (die er niet bij is getekend), de centrale lijn en de
regressielijn.
Bepaal zo goed mogelijk daaruit de waarde van r. |
 |
| |
|
|
|
| |
|
|
|
| 8. |
De
lengte van een koperen staaf wordt gemeten bij verschillende
temperaturen.
Dat geeft de volgende tabel: |
| |
|
| |
| temperatuur (in ļC) |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
| lengte (in cm) |
180 |
187 |
191 |
192 |
197 |
203 |
205 |
212 |
213 |
|
| |
|
|
|
| |
a. |
Geef een vergelijking van de
regressielijn en bereken de correlatiecoŽfficiŽnt. |
| |
|
|
|
| |
b. |
Hoe groot is de som van de kwadraten van residuen? |
| |
|
|
|
| |
Voor een gouden staaf geldt de regressielijn L = 0,75T + 160 en
een correlatiecoŽfficiŽnt van 0,84. De gemiddelde temperatuur
van de metingen was 40ļC, net als bij de koperen staaf
hierboven. |
| |
|
|
|
| |
c. |
Geef een vergelijking van de centrale lijn. |
| |
|
|
|
| 9. |
examenvraagstuk VWO Wiskunde A, 1993. In een Amerikaans laboratorium heeft men
proeven genomen waarbij gelet werd op het verband tussen de hoogte van
de bewaartemperatuur (F) in graden Fahrenheit en de werkzaamheid
(W) van een bepaald geneesmiddel. Bij temperaturen van 30ļ, 50ļ, 70ļ en
90ļ (Fahrenheit) werden drie porties van gelijk gewicht uit eenzelfde
productie 20 dagen bewaard. Na deze periode werd op identieke wijze de
werkzaamheid van de porties vastgesteld. De werkzaamheid werd uitgedrukt
in percentages van de werkzaamheid zoals die was voor het bewaren.
In de volgende tabel waar de twaalf meetresultaten zijn weergegeven, kan
onder andere worden afgelezen dat de drie porties die bij een
temperatuur van 30ļ werden bewaard achtereenvolgens 39%, 42% en 35% van
hun oorspronkelijke werkzaamheid hadden. |
| |
|
|
|
| |
| bewaartemp. (F) |
30ļ |
50ļ |
70ļ |
90ļ |
| werkzaamheid (W) |
39, 42, 35 |
32, 26, 33 |
19, 27, 23 |
14, 19, 21 |
|
| |
|
|
|
| |
Indien men een rechtlijnig verband
veronderstelt, levert dit voor de regressielijn van W op F de
vergelijking
W = -0,35F + 48,30. |
| |
|
|
|
| |
a. |
Verwerk de gegevens van de tabel
in een spreidingsdiagram en teken daarin de regressielijn. |
| |
|
|
|
| |
b. |
Bereken de correlatiecoŽfficiŽnt
tussen W en F. |
| |
|
|
|
| |
Het verband tussen de
temperatuur in graden Fahrenheit (F) en in graden Celsius (C) wordt
vastgelegd door
F = 1,8C + 32.
De regressielijn van W op C heeft de gedaante W = aC + b
waarbij de bewaartemperatuur in graden Celsius wordt gemeten. |
| |
|
|
|
| |
c. |
Bereken a en b in
twee decimalen nauwkeurig. |
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|