|
||||||||||||||||||||||||||||||||||||||
| 1. | L1 = 1 - 2 - 3 - 3 -
5 - 6 L2 = 7 - 5 - 3 - 6 - 5 - 3 stat calc linreg(ax + b) (L1, L2) geeft r = -0,648 |
|||||||||||||||||||||||||||||||||||||
| 2. | a. | L1 = 16 - 17 - 17 - 18 - 19 - 20
- 22 L2 = 9 - 10 - 11 - 10 - 12 - 11 - 13 stat calc linreg(ax + b) (L1, L2) geeft r = 0,864 |
||||||||||||||||||||||||||||||||||||
| b. | L3 = 1,8 * L2 + 32 stat calc linreg(ax + b) (L1, L3) geeft weer r = 0,864 |
|||||||||||||||||||||||||||||||||||||
| 3. | Dx
en Dy
van dat ene punt zijn nul dus alle afwijkingen (ΣΔx2,
ΣΔy2 en
ΣΔxΔy) blijven gelijk. Het enige dat verandert is n (het aantal metingen) Voor de standaarddeviaties van x en y wordt beiden gedeeld door √n, dus σx ē σy wordt gedeeld door n Voor de covariantie wordt ook door n gedeeld. Teller en noemer van r worden beiden door n gedeeld, dus r blijft gelijk! |
|||||||||||||||||||||||||||||||||||||
| 4. | Voor een horizontale
lijn is voor alle punten
Δy = 0 want
yi = ygemiddeld. Dan is σy ook gelijk aan nul. En ook de covariantie is nul. r wordt dan nul gedeeld door nul, en dat is ongedefinieerd. Men heeft gekozen voor r = 0 omdat, als alle y gelijk zijn, de waarde van x kennelijk geen enkele invloed op y heeft. |
|||||||||||||||||||||||||||||||||||||
| 5a. | x gemiddeld is
2, en y gemiddeld = (6 + p)/3 = 2 +
1/3p. Dat geeft deze tabel met afwijkingen: |
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
| uit de sommen van de laatste drie rijen kunnen we r bepalen: | ||||||||||||||||||||||||||||||||||||||
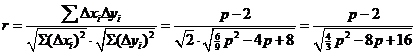 |
||||||||||||||||||||||||||||||||||||||
| 5b. | Met de quotiŽntregel en de kettingregel: | |||||||||||||||||||||||||||||||||||||
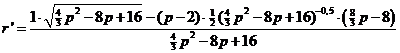 |
||||||||||||||||||||||||||||||||||||||
| Dat is nul als de teller nul is: | ||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
| Vermenigvuldig alles met die wortel: | ||||||||||||||||||||||||||||||||||||||
| 4/3p2
- 8p + 16 - 1/2(p - 2)(8/3p
- 8) = 0 4/3p2 - 8p + 16 - 4/3p2 + 4p + 8/3p - 8 = 0 -4/3p + 8 = 0 p = 6 (en dat geeft r = 1) Dat had je kunnen verwachten want de punten (1, 2) (2, 4) en (3,6) liggen precies op een rechte lijn. |
||||||||||||||||||||||||||||||||||||||
| 6. | De x en de y staan symmetrisch in de formule voor r, dus als je ze omwisselt dan blijft r gelijk. | |||||||||||||||||||||||||||||||||||||
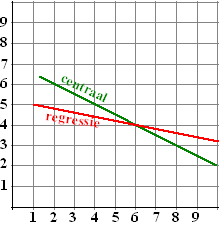
| 7. | De regressielijn gaat
door bijv. (1, 5) en (6, 4) De helling is dan (4 - 5)/(6 - 1) = -0,2 De centrale lijn gaat door bijv. (2, 6) en (6,4) De helling is dan (4 - 6)/(6 - 2) = -0,5 Dat geeft -0,2 = r ē -0,5 dus r = 0,4 |
 |
||||||||||||||||||||||||||||||||||||
| 8. | a. | stat - edit temperaturen in L1, lengtes in L2. stat - calc - linreg(ax + b) geeft regressielijn L = 0,82T + 164,97 en correlatiecoefficient r = 0,9917 |
||||||||||||||||||||||||||||||||||||
| b. | list - resid - sto -
L3 L4 = L3^2 list - sum L4 geeft som 16,96 |
|||||||||||||||||||||||||||||||||||||
| c. | a = 0,75
en r = 0,84 geeft voor de helling van de centrale
lijn a/r = 0,8929 T = 40 geeft L = 0,75 ē 40 + 160 = 190 dus de centrale lijn gaat door (40, 190) 190 = 0,8929 ē 40 + b geeft dan b = 154,284 De centrale lijn is L = 0,8929T + 154,284 |
|||||||||||||||||||||||||||||||||||||
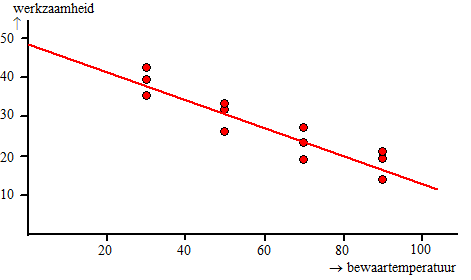
| 9. | a. |
|
||||||||||||||||||||||||||||||||||||
| b. | stat - edit zet de temperaturen in L1 en de werkzaamheden in L2 stat - calc - linreg(ax + b) (L1, L2) geeft de regressielijn W = -0,347F + 48,3 en de correlatiecoŽfficiŽnt r = -0,926 |
|||||||||||||||||||||||||||||||||||||
| c. | F = 1,8C + 32 W = -0,347F + 48,3 wordt dan W = -0,347 ∑ (1,8C + 32) + 48,3 W = -0,62C + 37,20 Dus a = -0,62 en b = 37,20 |
|||||||||||||||||||||||||||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
||||||||||||||||||||||||||||||||||||||