| |
 |
| Combinaties. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
Neem het volgende probleem:
|
|
Een korporaal is leider van een groep van 8
soldaten. Hij wijst voor de komende verkenningsmissie drie
vrijwilligers aan. Op hoeveel manieren kan hij dat doen? |
|
Je zou misschien zeggen: voor de eerste van de groep zijn er 8
mogelijkheden, daarna voor de tweede nog 7 en tenslotte voor de derde
nog 6, dus dat geeft in totaal 8 7 6 = 336 mogelijkheden
(dat is trouwens 8 nPr 3).
Maar dan heb je een denkfout gemaakt!
Laten we de soldaten A tm H noemen, en al die groepjes van 3 gaan
opschrijven. Dit zou het papiertje van de korporaal kunnen zijn: |
|
|
ABC
ABD
ABE
ABF
ABG
ABH
ACB
ACD
ACE
ACF
ACG
ACH
ADB
ADC
ADE
... |
BAC
BAD
BAE
BAF
BAG
BAH
BCA
BCD
BCE
BCF
BCG
BCH
BDA
BDC
BDE
... |
CAB
CAD
CAE
CAF
CAG
CAH
CBA
CBD
CBE
CBF
CBG
CBH
CDA
CDB
CDE
... |
DAB
DAC
DAE
DAF
DAG
DAH
DBA
DBC
DBE
DBF
DBG
DBH
DCA
DCB
DCE
... |
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
... |
|
|
|
|
Daar staan in totaal dus 336
groepjes.
Maar er zitten DUBBELEN bij!!!!
Je ziet bijvoorbeeld op het papiertje hierboven groepje ACD er al zes
keer opstaan. En dat is natuurlijk zes keer het zelfde groepje dat op
verkenning zal gaan. Dat komt omdat de volgorde waarin de soldaten
worden gekozen NIET van belang is, het gaan er alleen om wie er gekozen
worden. Je moet dit groepje natuurlijk niet 6 keer meetellen, maar
slechts 1 keer.
Maar wacht eens even.....
ELK groepje staat er op deze manier zes keer in. Het totaal aantal echt
verschillende groepjes dat we hebben gevonden is dus zes keer te groot,
dus in werkelijkheid zijn er 336/6 = 56
verschillende groepjes mogelijk. |
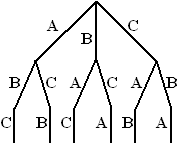
Dat getal 6 komt natuurlijk van
het aantal manieren waarop drie letters gerangschikt kunnen worden. Voor
de eerste letter zijn er 3 mogelijkheden, daarna voor de tweede nog 2,
en tenslotte voor de laatste nog 1. Dat geeft in totaal 3 2 1 =
6 mogelijkheden.
Het mini-boompje hiernaast laat dat zien.
Dit aantal groepjes waarbij de volgorde dus NIET van belang is, heet het
aantal combinaties van 3 uit 8. |
|
|
|
combinaties
kies k dingen uit een verzameling van n
de volgorde is niet van belang
het is zonder terugleggen |
|
|
|
| Je berekent het aantal combinaties
door het aantal permutaties te delen door het aantal dubbelen k! (zoals
hierboven gedeeld moest worden door 3! = 6). |
|
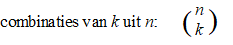 |
|
|
Je noteert het aantal combinaties
van k uit n met twee getallen tussen haakjes zoals
hierboven, en je spreekt het uit als "n boven k"
of "n over k"
Ook op je rekenmachine is uiteraard weer een knop voor de combinaties te
vinden: de nCr knop.
Houd goed het verschil tussen permutaties en combinaties in de gaten: |
|
|
combinaties: de volgorde is NIET
van belang; het zijn groepjes
permutaties: de volgorde is WEL
van belang; het zijn rijtjes |
|
|
|
| 1. |
Een grote supermarktketen
gaat zijn producten "labelen". Dat doen ze door op elk
product een stickertje te plakken van een vierkant van 4 bij 4
hokjes die zwart of geel gekleurd kunnen zijn. |

|
| |
|
|
|
a. |
Hoeveel codes zijn er mogelijk met 10
gele en 6 zwarte hokjes, zoals hiernaast? |
| |
|
|
|
b. |
Hoeveel codes zijn er in totaal
mogelijk? |
| |
|
|
|
|
|
|
|
| 2. |
De symbolen die in het
display van een elektrische wekkerradio verschijnen zijn opgebouwd uit één
of meer strepen van een rooster van 7 strepen: |
|
|
|
|
|
 |
|
|
|
|
| |
Bij de "6" hierboven staan
6 van de 7 strepen AAN, en bij de "1" maar 2 van de 7.
Hoeveel verschillende symbolen zijn in totaal mogelijk met 5
strepen AAN? (het hoeven uiteraard geen bestaande symbolen te
zijn, alles mag). |
| |
|
|
|
|
|
|
|
| 3. |
Een volleybalclub bestaat
uit 12 leden: 3 meisjes en 9 jongens.
Op trainingsavonden worden oefenwedstrijden gespeeld, waarbij de
club wordt opgesplitst in twee partijen van elk zes leden.
Hoeveel opsplitsingen zijn er waarbij niet alle meisjes bij
elkaar in het team zitten? |
| |
|
|
|
|
|
|
|
| 4. |
Een sultan heeft een
harem met daarin 14 vrouwen. Elke nacht laat hij aan het begin
een groepje van 4 vrouwen zijn slaapkamer binnenkomen om de
nacht mee door te brengen.
De sultan wil voor de afwisseling graag elke keer een ander
groepje.
Hoeveel nachten kan hij dat volhouden? |
| |
|
|
|
|
|
|
|
| 5. |
examenvraagstuk
HAVO wiskunde A, 1990
Een planoloog wil graag weten op grond van welke eigenschappen
de bewoners de straten van hun wijk beoordelen. Als onderdeel
van zijn onderzoek legt hij een aantal proefpersonen groepjes
van drie straten voor. Hij vraagt hen bij elk groepje aan te
wijzen welke twee van de drie straten het meest op elkaar
lijken.
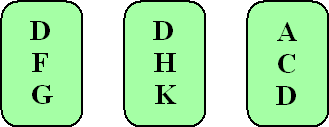
Het onderzoek heeft betrekking op 10 straten, voor het gemak A,
B, C, D, E, F, G, H, K, L genoemd. Hieruit worden alle mogelijke
groepjes van 3 gevormd en elk groepje wordt op alfabetische
volgorde op een kaartje geschreven. Hieronder zie je drie
voorbeelden. |
|
|
|
|
|
|
|
|
|
|
|
a. |
Hoeveel kaartjes zijn er nodig? |
| |
|
|
|
b. |
Op hoeveel kaartjes komt straat A
voor? |
| |
|
|
|
|
c. |
Op hoeveel kaartjes komen de straten A en B samen
voor? |
|
| |
|
|
|
|
|
|
|
|
De proefpersoon gaat bij
elk kaartje een keuze voor twee van de drie straten maken. |
|
|
|
|
|
d. |
Onderzoek of het mogelijk
is dat hij 7 keer voor de combinatie AB, 7 keer voor de
combinatie AC en 7 keer voor de combinatie AD kiest. |
| |
|
|
|
|
|
|
|
| 6. |
In een stoppenkast zitten
8 schakelaars die allemaal een stroomgroep bedienen. Deze
schakelaars hebben allemaal twee standen:
een AAN- stand en een UIT-stand. |
 |
| |
|
|
|
a. |
Op hoeveel manieren kunnen er vijf
van acht schakelaars in de AAN-stand staan? |
| |
|
|
|
b. |
Hoeveel manieren zijn er in totaal
mogelijk om de schakelaars in een willekeurige stand te zetten? |
| |
|
|
|
|
|
|
|
| 7. |
Een leraar begint elk
jaar met 3 moppen te vertellen.
Dat doet hij al 21 jaar lang, maar hij heeft nog nooit dezelfde
3 moppen verteld.
Toon aan dat hij met dezelfde moppenvoorraad nog minstens 14
jaar door kan zonder dezelfde drie te vertellen. |
| |
|
|
|
| 8. |
Een klein jongetje gaat
zijn verjaardag vieren, en hij mag van zijn ouders 8 vriendjes
uitnodigen. Helaas heeft hij 12 vriendjes, dus hij zal moeten
kiezen. |
| |
|
|
|
| |
a. |
Op hoeveel manieren kan
hij kiezen wie hij uitnodigt? |
| |
|
|
|
| |
Op zijn feestje geven ze
hem één voor één een cadeautje. |
| |
|
|
|
| |
b. |
Hoeveel
verschillende volgorden zijn er voor hem om de cadeautjes te
krijgen? |
| |
|
|
|
| |
|
|
|
| 9. |
Een leraar gaat in zijn
klas van 28 leerlingen 4 verschillende boeken verloten. |
| |
|
|
|
| |
a. |
Op hoeveel manieren kan
hij de boeken verloten als niemand meer dan 1 boek krijgt? |
| |
|
|
|
| |
b. |
Op hoeveel manieren kan
het als er wel leerlingen meerdere boeken mogen krijgen? |
| |
|
|
|
| |
c. |
Op hoeveel manieren kan
het als de boeken hetzelfde zijn, en elke leerling weer
hoogstens één boek mag krijgen? |
| |
|
|
|
| |
|
|
|
| 10. |
Een klas bestaat uit 15
meisjes en 12 jongens. Ze gaan een feestavond houden.
Daarvoor moet er een schoonmaakploeg van 8 leerlingen worden
gekozen. |
| |
|
|
|
| |
a. |
Op hoeveel manieren kan
men zon schoonmaakploeg kiezen? |
| |
|
|
|
| |
b. |
Op hoeveel manieren kan
men zon schoonmaakploeg kiezen als er 2 meisjes en 6 jongens
in moeten zitten? |
| |
|
|
|
| |
Voor de organisatie van een feestavond worden uit de
overgebleven leerlingen nog drie leerlingen aangewezen. De
eerste leerling verzorgt de muziek, de tweede de drank en de
derde de hapjes. |
| |
|
|
|
| |
c. |
Op
hoeveel manieren kan men deze leerlingen kiezen? |
| |
|
|
|
| |
|
|
|
| |
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TOEPASSING:
ANAGRAMMEN |
|
|
Een anagram van een woord is een
ander woord dat je kunt maken door de volgorde van de letters te
veranderen.
Zo kun je van "TAK" bijvoorbeeld
"KAT" maken, maar ook de niet-bestaande woorden KTA, ATK,
AKT en TKA.
In totaal zijn er zes anagrammen van "KAT" (kenners zien
natuurlijk direct hier het aantal permutaties: 3!).
Het wordt anders als sommige letters vaker voorkomen.
Van OOK zijn er bijvoorbeeld alleen maar OKO en KOO; geen 6
maar slechts 3.
Neem het woord "HOTTENTOTTEN"
We gaan bekijken op hoeveel manieren we de letter van HOTTENTOTTEN door
elkaar kunnen zetten.
Hoeveel woorden zijn er met de letters E, E, H, N, N, O, O, T, T,
T, T, T te maken?
Laten we proberen zo'n woord te gaan fabriceren.
Dat kan op twee manieren:
Methode 1: zet de letters stuk voor stuk op hun plaats.
Laten we beginnen met 12 stippen waar deze twaalf letters uiteindelijk
moeten komen te staan: |
|
|
|

|
|
|
Laten we nu de beide E's op een
plaats zetten. Daarvoor moeten we 2 plaatsen uitkiezen uit de 12 om zo'n
E op neer te zetten. Maar wacht eens even:
|
kies er 2 uit de 12
zonder terugleggen
de volgorde is NIET van belang |
|
Dat kan dan op (12 nCr 2) manieren. Dat zijn er 66.
Goed, stel dat we twee plaatsen voor de E hebben gekozen: |
|
|
|
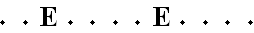
|
|
|
Voor de letter H zijn er daarna
nog 10 mogelijkheden. (eigenlijk (10 nCr 1) want je kiest er 1 uit
de 10)
Samen zijn er al 66 10 = 660 mogelijkheden voor de letters EEH. Een
mogelijkheid is: |
|
|
|
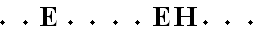
|
|
|
Dan moet je voor de twee N's
kiezen uit 9 plaatsen, dus dat kan op (9 nCr 2) = 36 manieren.
Daarna voor de 2 O's (7 nCr 2) = 21 manieren.
Tenslotte zijn er nog 5 plaatsen over voor de T's; dat kan maar op één
manier.
In totaal geeft dat 66 10 36 21 1 = 498960
manieren. Eigenlijk komt dat dus van:
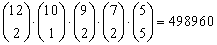
En als je de volgorde verandert geeft dat het zelfde resultaat. Laten we
letters in omgekeerde volgorde op hun plek zetten, dan geeft dat:
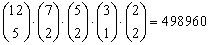
Inderdaad hetzelfde resultaat. |
|
|
| Methode 2: tel de
dubbelen. |
|
|
Er moeten 12 letters in een
volgorde gezet worden. Dat kan in principe op 12! manieren.
Nu gaan we delen door de dubbelen:
- Er zijn twee E's, dus delen door 2!
- Er zijn twee N's, dus delen door 2!
- Er zijn twee O's dus delen door 2!
- Er zijn vijf T's dus delen door 5!
Dan blijft er over: |
|
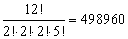
|
|
|
| 11. |
Hoeveel
anagrammen zijn er van het woord VERVELLEN? |
|
|
|
| |
|
| 12. |
Twee bridge
teams (A en B) spelen een wedstrijd over 28 spellen tegen
elkaar. De wedstrijdvorm is "board-a-match" en dat
betekent dat elk spel kan eindigen in winst (voor team A) of
verlies (voor team A) of gelijk spel.
In deze wedstrijd blijkt team A 10 spellen te winnen, 12
te verliezen en op 6 spellen is het remise.
Op hoeveel mogelijke manieren kan dit resultaat tot stand komen?
|
| |
|
|
|
|
|
| 13. |
Een gezin van
maar liefst 12 kinderen bestaat uit 8 jongens en 4 meisjes.
Hoeveel mogelijke gezinsopbouwen (als je alleen let op jongen of
meisje naar leeftijd) zijn er voor zo'n gezin? |
| |
|
|
|
|
|
| 14. |
De
International Darts League (IDL) was jarenlang een
dartstoernooi in Nijmegen. Na een aantal voorrondes en
kwartfinales en halve finales spelen de laatste twee
overgebleven darters een finale. Daarvoor geldt een "Best-of-
25". Dat betekent dat de eerste die 13 sets wint de
winnaar is.
In 2006 won onze eigen Raymond van Barneveld de IPC van Colin Lloyd met 13-5 en won daarmee 30000. |
|
Hoeveel
wedstrijdverlopen kunnen leiden naar de eindstand van 13-5 winst
voor onze Raymond? (denk erom dat Raymond in ieder geval de
laatste set moest winnen!) |
| |
|
|
|
|
|
|
|
| 15. |
Iemand heeft
zin om een alternatief potje schaak te spelen.
Hij wil de stukken op de achterste rij in een willekeurige
beginvolgorde zetten (zowel voor zwart als voor wit). Alles is
daarbij toegestaan, dus ook bijvoorbeeld twee dezelfde kleur
lopers zoals zwart in het voorbeeld hiernaast heeft.
Hoeveel verschillende beginopstellingen zijn er mogelijk?
|

|
|
|
|
|
|
|
|
|
| 16. |
Een lange trein bestaat uit de
volgende wagons:
1 locomotief
5 goederenwagons
10 eersteklas passagierswagons
12 tweedeklas passagierswagons
3 restauratiewagons.
De locomotief moet uiteraard vooraan, maar verder kunnen alle
wagons willekeurig achter elkaar geschakeld worden.
Hoeveel mogelijke treinen zijn er te maken? |
| |
|
|
|
| |
|
|
|
| 17. |
Een wijnliefhebber drinkt
in de maand november samen met zijn vrouw elke dag een fles wijn
leeg. Ze drinken alleen rode en witte wijn. Al hun flessen rode
wijn zijn hetzelfde, en ook al hun flessen witte wijn zijn
gelijk. |
| |
|
|
|
| |
a. |
Op hoeveel manieren kunnen zij deze
maand wijn drinken als ze van beide soorten 30 flessen hebben? |
| |
|
|
|
| |
b. |
Op hoeveel manieren kunnen zij deze
maand wijn drinken als zij 10 flessen witte wijn hebben en 20
flessen rode wijn? |
| |
|
|
|
| |
 c. c. |
Op hoeveel manieren kunnen zij deze
maand wijn drinken als zij 20 flessen rode wijn en 12 flessen
witte wijn hebben? |
| |
|
|
|
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
|
|
|
|
|
|