|
|
 |
|
De omtrek van een Cirkel. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
Over de omtrek van een cirkel
hoef ik gelukkig niet moeilijk te doen. Daar is gewoon een kant-en-klare
formule voor.
De omtrek hangt natuurlijk af van de grootte van de cirkel, dus van de
straal.
Deze formule geldt: |
| |
|
|
|
|
|
| |
|
|
|
| Daarin is r de straal van
die cirkel. |
|
| |
|
|
|
Leuk Voorbeeldje??
Iemand heeft een touw om de aarde gespannen en dat goed strak getrokken.
Neem aan dat de aarde een bol is en dat de omtrek 42000 km is.
Dat touw is dus 42000 km lang en ligt nu in een cirkel om de aarde.
Hij knipt het touw door en knoopt er een extra meter touw tussen.
Daardoor is het touw dus iets te ruim voor de aarde.
Het staat daardoor nu overal iets van het oppervlak van de aarde af.
Hoe ver er vanaf?
Oplossing.
De omtrek is 42000 km
dus de straal is 42000/2π
= 6684,50761 km
De nieuwe omtrek is 42000,001 km (1 m extra)
dus de nieuwe straal is 42000,001/2π
= 6684,50777 km.
Dat scheelt 6684,50777 - 6684,50761 = 0,00016 km en dat is 16 cm.
TOCH NOG VRIJ VEEL, VIND JE NIET??? |
 |
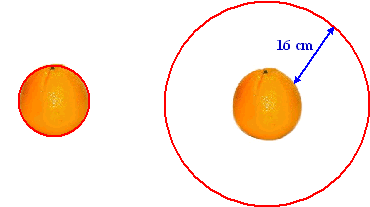
En het grappige is: die afstand 16 cm is bij elke cirkel gelijk! Of je
zo'n touw nou om de aarde spant of om een sinaasappel, als je er een
meter tussen doet staat het altijd 16 cm van het oppervlak af. |
| |
|
|
|
|
 |
| |
|
|
|
| |
|
|
|
| 1. |
Toon aan dat deze afstand inderdaad voor elke
cirkel gelijk is. |
| |
|
|
|
|
| |
|
|
|
Nou goed, verder is er aan deze
formule niet zoveel te beleven.
Het wordt pas interessant als lijnen cirkels gaan raken. Dus als je maar
een deel van de omtrek wilt weten.
Een belangrijke eigenschap van een lijn die een cirkel raakt is: |
| |
|
|
|
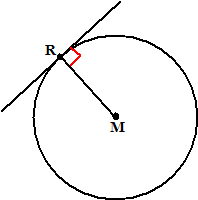
| Een raaklijn aan een cirkel staat loodrecht op de
straal. |
|
| |
|
|
|
Daarbij is de straal dan
natuurlijk het lijnstuk van het raakpunt R naar het middelpunt M van de
cirkel. Je moet er die tekening hiernaast bij in gedachten hebben. De
rood aangegeven hoek is een rechte hoek.
Dat heeft gevolgen voor allerlei situaties waarin touwen om cirkels zijn
gespannen (of waar cirkels in andere figuren zijn "ingeschreven", dat is
hetzelfde). |
 |
| |
|
|
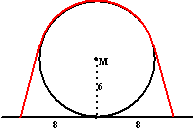
Hiernaast zie je een cirkel met straal 6, waar een rood
touw overheen is gespannen, waarvan de eindpunten afstand 16 uit elkaar
liggen. De figuur is symmetrisch.
.
De vraag is: "Hoe lang is het touw?" |
 |
| |
|
Nou, met de vorige
raaklijnfiguur in gedachten teken je natuurlijk meteen die lijnen vanaf
de raakpunten naar het middelpunt. Zoals hiernaast dus.
Omdat de cirkel de
grond raakt is hoek MQP ook recht, dus geldt Pythagoras in driehoek MPQ
:
62+ 82 = MP2 geeft MP = 10
Maar omdat de hoek bij R ook recht is, geldt ook in driehoek MRP
Pythagoras: 62 + PR2 = 102
Dat geeft PR = 8. (Dat hadden we trouwens ook wel sneller
kunnen zien: de driehoeken MPQ en MPR zijn gelijk)
Als PR = 8, dan is ook dat stuk aan de andere kant van naar de grond
toe gelijk aan 8. |
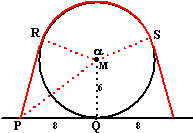 |
Blijft over het stuk RS. Dat is een deel van de cirkelomtrek.
Welk deel?
Dat hangt van de hoek
α af. Als we
weten hoeveelste deel
α van 360º is, dan weten
we ook hoeveelste deel van de hele omtrek dat rode touw is.
Nou kunnen we gelukkig (met sos-cas-toa) de hoeken van een 6-8-10
driehoek berekenen.
Dat geeft dat voor hoek PMR geldt: tan(PMR) = 8/6
en dan is PMR = 53,13°
Bij punt M komen vier zulke hoeken van 53,13° plus hoek α bij elkaar,
dus is α
= 360° - 4 · 53,13° = 147,48º
De hele omtrek van de cirkel is 2π ·
6 = 12π =
37,70
Dus deel RS is 147,48/360 · 37,7 =
15,44.
Het hele touw is dan 8 + 8 + 15,44 = 31,44 lang. |
| |
|
|
|
|
lengte van een deel van een
cirkelomtrek?
bereken de hoek naar het middelpunt! |
|
| |
|
|
|
| |
|
|
|
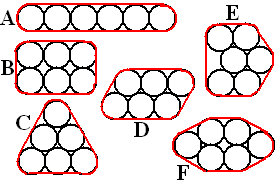
| 2. |
Zes
blikjes cola worden tegen elkaar aangeschoven en daarna gaat er een rode
rubber band omheen. Hiernaast zie je zes verschillende mogelijkheden om
dat te doen.
Bereken voor elk van die mogelijkheden de lengte van de rubberen
band, als de straal van een blikje cola 3 cm is. |
 |
| |
|
|
|
A: 60 + 6π
BCDF: 36 + 6π
E: 24+6π+6√3 |
|
| |
|
|
|
| 3. |
4
jongetjes staan op een plein op een rechte lijn, met onderlinge afstand
1 meter.
P wil naar S lopen, maar moet steeds minstens 1 meter van Q en van
R afblijven.
Hoe lang is zijn kortste route? |
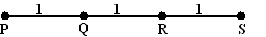 |
| |
|
|
|
|
|
|
|
| 4. |
Examenvraagstuk HAVO
Wiskunde B, 2000. |
| |
|
|
|
| |
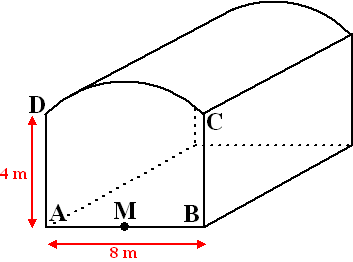
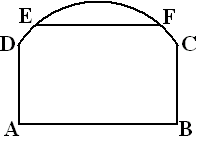
In Nederland zie je op bedrijventerreinen
vrij grote overeenkomsten in de dakvormen van fabriekshallen,
opslagloodsen en werkplaatsen. Een werkplaats met een veel
voorkomende dakvorm is te zien in de figuur hiernaast.
De vloer van deze werkplaats heeft de vorm
van een rechthoek.
Het dak heeft een gebogen vorm: in het vooraanzicht is boog CD een kwart
deel van de cirkel waarvan het middelpunt M het midden van AB is.
De breedte van AB is 8 meter.
De hoogte AD = BC is 4 meter |
 |
| |
a. |
Bereken de lengte van
boog CD. Geef je antwoord in gehele centimeters nauwkeurig. |
| |
|
|
|
| |
Ter versteviging van de dakconstructie is
op een aantal plaatsen op 5 meter hoogte een stalen dwarsbalk
aangebracht. |
| |
In de figuur hiernaast zie je een
vooraanzicht van de werkplaats met daarin zo'n dwarsbalk EF. |
 |
| |
|
|
| |
b. |
Bereken de lengte van EF. Geef je
antwoord in gehele centimeters nauwkeurig. |
| |
|
|
|
| |
|
|
|
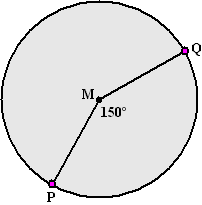
| 5. |
Een groot cirkelvormig
plein heeft straal 40 meter
Iemand moet van punt P op de rand naar punt Q op de rand lopen,
waarbij de hoek tussen PM en QM gelijk is aan 150º.
Hij gaat kiezen uit twee mogelijkheden:
I: van P naar M naar Q in twee rechte lijnen.
II: via de rand van P naar Q. |
 |
| |
|
|
| |
a. |
Bereken hoeveel procent de tweede
route langer is vergeleken met de eerste. |
| |
|
|
| |
b. |
Bij welke punten Q op de rand is de
tweede route korter? |
| |
|
|
|
| |
|
|
|
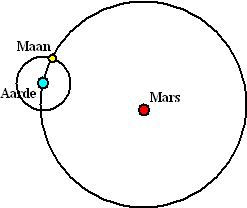
| 6. |
Kan een astronaut op
Mars met het blote oog de Aarde en de Maan van elkaar
onderscheiden?
Gegevens:
Je kunt twee hemellichamen met het blote oog van elkaar
onderscheiden als de kijkhoek ertussen ongeveer 2 minuten is. 1
minuut is 1/60
graad.
afstand Aarde-Mars als ze het dichtst bij elkaar staan:
78.000.000 km
afstand Aarde-Maan: 385.000 km
1 minuut is 1/60
graad
Hiernaast staat de situatie geschetst als de maan voor een
waarnemer op Mars op het punt het verst van de aarde af staat. |
 |
| |
|
|
|
| |
a. |
Hoeveelste deel van de
cirkel rondom Mars is het stukje Aarde-Maan ongeveer? |
| |
|
|
|
| |
b. |
Kan een astronaut op
Mars met het blote oog de Aarde en de Maan van elkaar
onderscheiden? |
| |
|
|
|
| 7. |
Kangoeroewedstrijd.
Een cirkel van straal 1 rolt over een lengte 11π
van START naar FINISH. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Hoe ziet de cirkel er uit als hij
in FINISH is aangekomen? |
| |
|
|
|
| |
 |
| |
|
|
|
| 8. |
Kangoeroewedstrijd.
Een cirkel met straal 4 is opgedeeld in vier gelijke gebieden
met stukjes cirkel van straal 2.
Wat is de omtrek van zo’n gebied?
|
 |
| |
|
|
|
| 9. |
Kangoeroewedstrijd.
Een munt met een diameter van 1 cm wordt over de buitenkant
van een regelmatige zeshoek gerold. De zijden van de
zeshoek zijn 1 cm.
In het midden van het muntstuk zit een gat waarin een
potlood is gestoken.
Dit beschrijft bij het rollen een baan om de zeshoek.
Hoe lang is die baan? |
 |
| |
|
|
|
| 10. |
Kangoeroewedstrijd.
De uurwijzer van een
klok is 4 cm lang, de minutenwijzer 8 cm. Wat is de verhouding
van de afstanden die de uiteinden van beide wijzers afleggen
tussen 2 en 5 uur 's middags? |
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|
| |
|
|
|