breuksplitsen


Breuksplitsen.	© h.hofstede (h.hofstede@hogeland.nl)

Kijk eerst nog even hoe het samennemen van breuken ging:

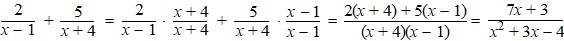De vraag is nu: als je dat eindantwoord krijgt, kun je dan die twee oorspronkelijke (simpelere) breuken vinden?
Ofwel:

"Kan het ook andersom?"

Het zal je niet verbazen dat het antwoord "JA" is, neem ik aan.
Het eerste wat je moet doen als je die eindbreuk aan de rechterkant ziet, is kijken of je de noemer kunt ontbinden.
Als je kunt vinden dat x² + 3x - 4 geschreven kan worden als (x - 1)(x + 4), dan ga je gewoon proberen of die hele breuk geschreven kan worden als ^A/_{(x
- 1)} + ^B/_{(x + 4)} en om dat te onderzoeken neem je die twee breuken gewoon weer samen, net zoals hierboven gebeurde:

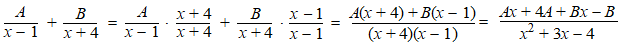Dat moet gelijk zijn aan de gegeven breuk, dus moet gelden: Ax + 4A + Bx - B = 7x + 3
Dat lijkt een vergelijking met veel te veel onbekenden.....

De oplossing presenteert zichzelf als je je maar bedenkt dat deze vergelijking voor ELKE x moet kloppen.
Als je bijvoorbeeld neemt x = 1, dan staat er A + 4A + B - B = 10 ⇒ 5A = 10 ⇒ A = 2 en daar is A al.
En als je neemt x = -4 dan staat er -4A + 4A - 4B - B = -25 ⇒ -5B = -25 ⇒ B = 5. KLAAR

Ik hoop dat je ziet dat die x = 1 en x = -4 niet zomaar toevallig zijn gekozen. Je kiest die natuurlijk zó, dat één van de letters A of B wegvallen.

Behalve dat "geprobeer" met x-waarden kan het ook wiskundig op de volgende manier iets netter:

Begin weer met Ax + 4A + Bx - B = 7x + 3 en groepeer nu de termen met x en die zonder x:
x(A + B) + (4A - B) = 7x + 3
Dat klopt alleen voor élke x als A + B = 7 en 4A - B = 3
Dat is een stelsel van twee vergelijkingen en dat is makkelijk op te lossen.

Wat kan er mis gaan?

Er gebeurt iets vreemds als die noemer als een kwadraat geschreven kan worden.
Voorbeeld:

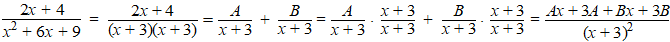Dus moet gelden Ax + 3A + Bx + 3B = 2x + 4
Als je nu volgens de eerste manier hierboven x = -3 neemt, dan staat er 0 = 4.
En op de tweede manier vind je: Ax + 3A + Bx + 3B = 2x + 4 ⇒ x(A + B) + (3A + 3B) = 2x + 4
Dat geeft het stelsel: A + B = 2 en 3A + 3B = 4, en dat valt niet op te lossen!!

Als je toch per se die breuk wilt splitsen, dan kun je dat als volgt doen:

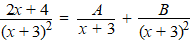Dat werkt, want als je die twee rechterbreuken samen wilt nemen, dan hoef je alleen van die eerste de teller en noemer met (x + 3) te vermenigvuldigen, en dan krijg je toch iets lineairs in die uiteindelijke teller. Kijk maar hoe het werkt:

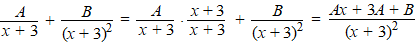Dat is gelijk aan de oorspronkelijke breuk als Ax + 3A + B = 2x + 4.
Groeperen: geeft in een keer het stelsel A = 2 en 3A + B = 4 ofwel A = 2 en B = -2

Het werkt zelfs nog algemener:

Daarin is P(x) een polynoom met graad die lager is dan de graad van de noemer.

Voorbeeld:

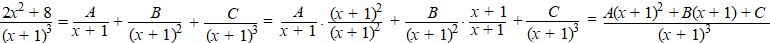⇒ A(x + 1)² + B(x + 1) + C = 2x² + 8
⇒ Ax² + 2Ax + A + Bx + B + C = 2x² + 8

Groepeer nu per macht van x: x² (A) + x(2A + B) + (A + B + C) = 2x² + 8

Dus A = 2 en 2A + B = 0 en A + B + C = 8
Dat geeft A = 2 en B = -4 en C = 10

Combineren maar!!!

Dit voorbeeld zal wel duidelijk maken hoe het werkt:

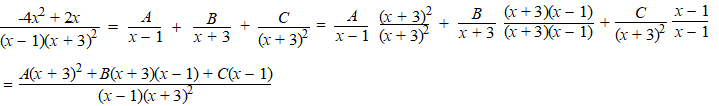⇒ A(x + 3)² + B(x + 3)(x - 1) + C(x - 1) = -4x² + 2x
⇒ Ax² + 6Ax + 9A + Bx² + 2Bx - 3B + Cx - C = -4x² + 2x
⇒ x² (A + B) + x(6A + 2B + C) + (9A - 3B - C) = -4x² + 2x
Dus A + B = -4 en 6A + 2B + C = 2 en 9A - 3B - C = 0
De eerste geeft A = -4 - B en invullen in de andere twee geeft: -24 - 4B + C = 2 en -36 - 12B - C = 0
De eerste geeft nu C = 4B + 26 en dat kun je invullen in de tweede: -62 - 16B = 0 ⇒ B = ^-62/₁₆ = ^-31/₈
Dan is C = ²¹/₂ en A = ^-1/₈


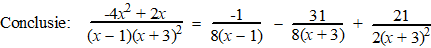1.	Splits de volgende breuken:

	a.	e.

	b.	f.

	c.	g.

	d.	h.



© h.hofstede (h.hofstede@hogeland.nl)