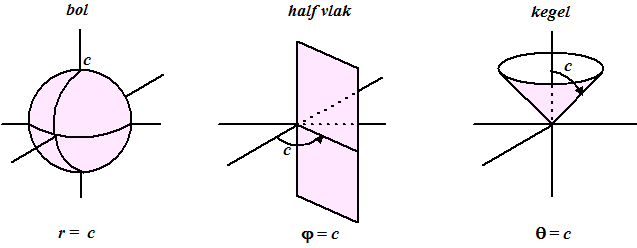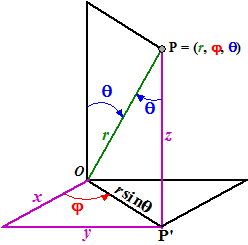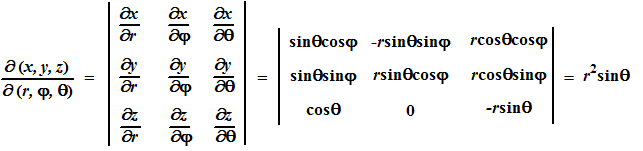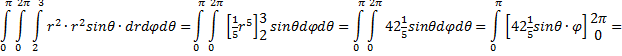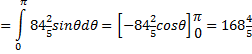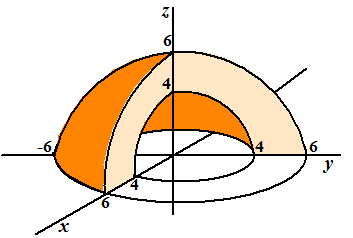Bolcoordinaten

© h.hofstede (h.hofstede@hogeland.nl)

Bolcoördinaten.

Na rechthoekige coördinaten en cilindercoördinaten zijn we nu toe aan de derde manier om ruimtelijke problemen te beschrijven, en dat zijn bolcoördinaten.
Die werken meestal het best als je te maken hebt met puntsymmetrische problemen (cilindercoördinaten waren vooral handig voor lijnsymmetrische problemen, weet je nog?).

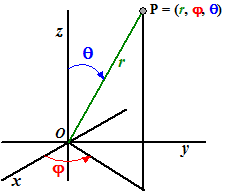
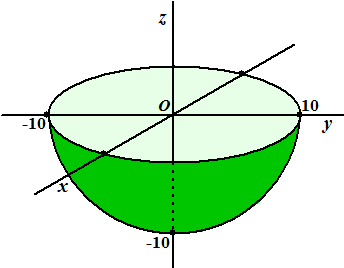
Het werkt als in de figuur hiernaast.
Om een punt in de ruimte aan te geven gebruiken we twee hoeken en een afstand.

r is de afstand OP tot de oorsprong

φ is de hoek in het Oxy- vlak met de positieve x-as (net als bij poolcoördinaten en cilindercoördinaten)

θ is de hoek van OP met de positieve z-as

De vergelijking van sommige gekromde vlakken kan daardoor erg veel eenvoudiger worden.
Hieronder zie je de drie simpelste:

Hiernaast zie je het verband tussen bolcoördinaten en rechthoekige coördinaten.
P' is de projectie van P in het grondvlak.
Vanwege de blauwe hoeken θ is dan OP'= rsinq en
z = rcosθ

In de driehoek met hoek j zie je dan dat
x = rsinθcosφ en y = rsinθsinφ

Daarmee kun je snel bolcoördinaten omrekenen in rechthoekige coördinaten.

x = rcosφsinθ
y = rsinφsinθ
z = rcosθ

Het omrekenen van rechthoekige coördinaten naar bolcoördinaten doe je meestal zó:
• Bereken r via r² = x² + y² + z²
• Bereken θ via cosθ =^z/_r
• Bereken φ via cosφ = ^x/_rsinθ Bedenk dat daarbij twee mogelijkheden zijn tussen 0 en 2π.
Aan de y kun je zien welke je moet hebben.


1.	Zet de volgende bolcoördinaten om in rechthoekige coördinaten.

	a.	A = (1, 0, ¹/₃π)

	b.	B = (4, ¹/₄π, ¹/₄π)

	c.	C = (2, -¹/₆π, π)

2.	Zet de volgende rechthoekige coördinaten om in bolcoördinaten. Rond indien nodig af op twee decimalen.

	a.	A = (1, 1, 1)

	b.	B = (√6, -√6, 2)

	c.	C = (2, 2√3, 4)

3.	Schets de vlakken waarvan hier de vergelijking in bolcoördinaten wordt gegeven:

	a.	r = sinθsinφ

	b.	rsinθ = 4

	c.	r = cosθ

Integralen met bolcoördinaten.

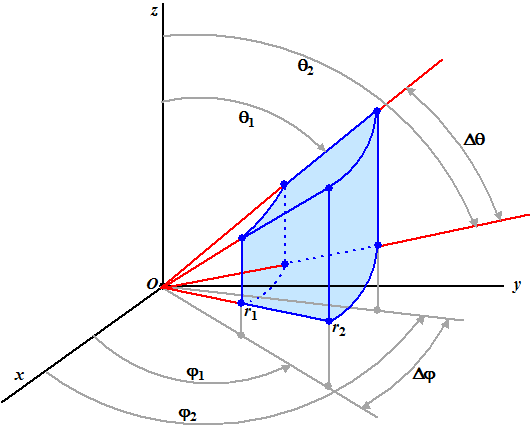
Als je met bolcoördinaten een integraal aan het uitrekenen bent, dan bereken je eigenlijk altijd die integraal over een bolschijfje zoals het blauwe bolstukje dat hieronder is geschetst.

Zoals je ziet varieert de hoek in het grondvlak (met de positieve x-as) tussen φ₁ en φ₂, en de hoek met de z-as tussen θ₁ en θ₂. De straal varieert van r₁ tot r₂.
De Jacobiaan (deze les) om dxdydz om te zetten in drdφdq bereken je zó

Die laatste stap moet je zelf maar narekenen.
Gewoon alles uitschrijven en een aantal keer gebruiken dat sin²α +cos²α = 1

Dat dat ongeveer zo is kun je als volgt zien: het kubusje met inhoud dxdydz gaat over in dat blauwe bolstukje. Daarvan zijn de afmetingen ongeveer rdθ (de hoogte) bij rsinθdφ (in de φ-richting) bij dr (richting de oorsprong) en daarvan is de inhoud rdθ • rsinθdφ • dr = r² sinθ • dθdφdr
Dus dxdydz = r² sinθ • dθdφdr
Vandaar die Jacobiaan....ongeveer....

Voorbeeld.
Bereken de integraal van f(x, y, z) = x² + y² + z² over de bolschil, die wordt ingesloten door twee bollen met middelpunt O en stralen 2 en 3.
Voor een hele bol loopt θ van 0 tot π en loopt φ van 0 tot 2π.
Omdat verder x² + y² + z² = r² geeft dat de volgende drievoudige integraal:

Bereken de integraal van f(x, y, z) = z
over het gekleurde lichaam hiernaast, waarvan de gekromde vlakken delen van bollen zijn.

15π

Bereken de integraal van f(x, y, z) = x² + y²
over de halve bol hiernaast.

Bedenk daarbij dat sin³x = (1 - cos²x) • sinx
Dus een primitieve van sin³x is -cosx + ¹/₃cos³x