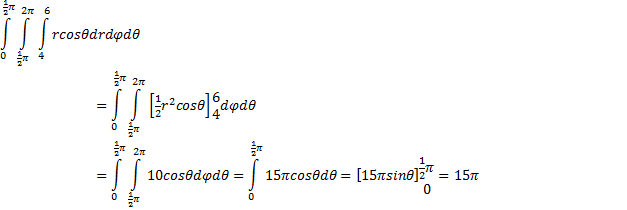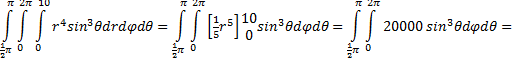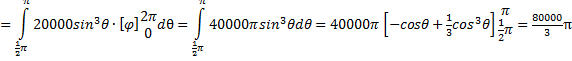|
|||||
| 1. | a. | x = 1• cos0 •
sin1/3π
= 1/2√3 y = 1 • sin0 • sin1/3π = 0 z = 1 • cos1/3π = 1/2 A = (1/2√3, 0, 1/2) |
|||
| b. | x= 4 • cos1/4π
• sin1/4π
= 2 y = 4 • sin1/4π • sin1/4π = 2 z = 4 • cos1/4π = 2√2 B = (2, 2, 2√2) |
||||
| c. | x = 2 • cos(-1/6π)
• sinπ = 0 y = 2 • sin(-1/6π) • cosπ = 1 z = 2 • cosπ = -2 C = (0, 1, -2) |
||||
| 2. | a. | r2
= 12 + 12 + 12 = 3 dus r
= √3 cosθ = 1/√3 geeft θ = 0,96 sinθ = √(1 - cos2θ) = √(2/3) cosφ = 1/(√3 • √2/3) = 1/2√2 dus φ = 1/4π of φ = 7/4π omdat y positief is de eerste. A = (√3, 1/4π, 0.96) |
|||
| b. | r2
= 6 + 6 + 4 = 16 dus r = 4 cosθ = 2/4 geeft θ = 1/3π dan is sinθ = 1/2√3 cosφ = √6/(4 • 0,5√3) = 1/2√2 dus φ = 1/4π of φ = 7/4π omdat y negatief is de laatste B = (4, 7/4π, 1/3π) |
||||
| c. | r2 =
4 + 12 + 16 = 32 dus r = √32
= 4√2 cosθ = 4/4√2 geeft θ = 1/4π dan is sinθ = 1/2√2 cosφ = 2/(4√2 • 0,5√2) = 1/2 dus φ = 1/3π of φ = 5/3π omdat y positief is de eerste B = (4√2, 1/3π, 1/4π) |
||||
| 3. | a. | r = sinθsinφ
= y/r dus r2 = y x2 + y2 + z2 = y x2 + y2 - y + z2 = 0 x2 + y2 - y + 1/4 + z2 = 1/4 x2 + (y - 1/2)2 + z2 = (1/2)2 Dat is een bol met straal 1/2 en middelpunt (0, 1/2, 0) |
|||
| b. | rsinθ
= 4 Dan is die schuine lijn OP' gelijk aan 4 (P' de projectie van P op het Oxy-vlak) Waar liggen al die punten P ? Op een cilinder met straal 4, en als as de z-as. |
||||
| c. | r = cosθ dan is r2 = rcosθ en dat is z r2 = x2 + y2 Dus x2 + y2 = z Cirkels waarvan de straal afhangt van z: Dat is een kegel met de top in de oorsprong, die omhoog gaat tot z = 1 |
||||
| 4. | Voor het lichaam
geldt: 4 < r < 6 en 1/2π < φ < 2π en 0 < θ < 1/2π Verder is z = rcosθ |
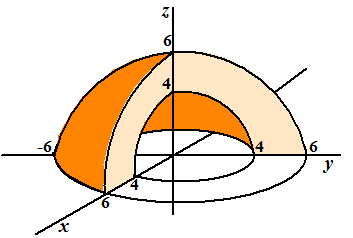 |
|||
|
|
|||||
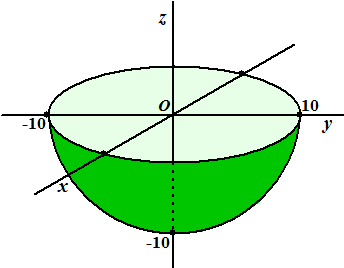
| 5. | Voor het lichaam
geldt: 0 < r < 10 en 0 < φ < 2π en 1/2π < θ < π Verder is x2 + y2 = r2sin2θcos2φ + r2sin2θsin2φ = r2sin2θ Met de Jacobiaan erbij wordt de integrand dan r2sin2θ • r2sinθ = r4sin3θ |
 |
|||
|
|
|||||
|
|
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||