|
|
 |
|
Bissectrice. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Een bissectrice van een hoek is
een lijn die die hoek doormidden deelt. Het heet daarom ook wel de
deellijn van die hoek. Ook zo´n bissectrice is een
meetkundige plaats.
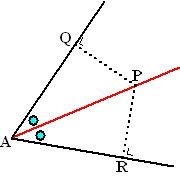
Dat kun je zien in de figuur hiernaast waarin de rode lijn een
bissectrice is.
Kies een willekeurig punt P op de bissectrice, en teken de loodlijnen PQ
en PR op de benen van de hoek. Dan geldt APQ ≅
APR (immers ∠QAP = ∠PAR en ∠PQA = ∠PRA en zijde AP
zit in beide driehoeken). Maar als die driehoeken congruent zijn, dan
geldt ook PQ = PR.
PQ en PR stellen de afstanden van punt P tot de benen van de hoek voor. |
 |
| |
|
| de bissectrice van een hoek is de verzameling punten die
gelijke afstanden tot de benen van die hoek hebben. |
|
| |
|
De bissectrice is dus een
conflictlijn, namelijk van beide benen van de hoek
Omdat we de afstand van een punt tot een lijn nodig hebben moeten we ons
daar eerst maar eens in verdiepen, lijkt me..... |
| |
|
|
De afstand van een punt tot een
lijn. |
| |
|
Stel dat P het punt (xP,
yP) is, en l de lijn ax + by =
c
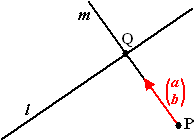
Stel dat m de lijn door P loodrecht op l is, en Q het
snijpunt van l en m |
 |
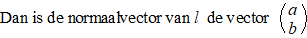 |
| Maar dat is de richtingsvector van m. |
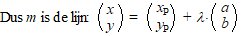 |
Een willekeurig punt van m
is dan te schrijven als (xP + aλ,
yP + bλ)
Om punt Q te vinden substitueren we dat punt in de vergelijking van l:
a(xP + aλ) +
b( yP +
bλ) = c
⇒
axP + a2λ
+ byP + b2λ
= c |
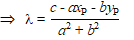 |
|
Maar nou komt het: die
λ zegt hoe vaak je de richtingsvector van
lijn m vanaf punt P moet nemen om in punt Q te komen.
Die richtingsvector heeft lengte
√(a2 + b2) dus
heeft lijnstuk PQ de lengte λ •
√(a2 + b2) |
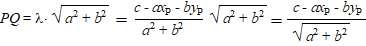 |
Daarmee hebben we een formule
voor de afstand PQ van P tot l gevonden!
Maar......
We hebben aan één ding niet gedacht. Het kan namelijk zijn dat de
λ die we vinden negatief is. In dat geval
vinden we een negatieve afstand PQ, en dat is eigenlijk niet de
bedoeling. We kunnen dat "repareren" door in de formule voor PQ de
absolute waarde te nemen van de teller. Dat geeft: |
| |
|
|
|
| |
|
Voorbeeld 1. Bereken de afstand van punt
(4,10) tot de lijn 2x + 6y = 5
|c - axP -
byP| =
|5 - 2 • 4
- 6 • 10|
= |-63|
= 63
√(a2 + b2)
= √40 dus de afstand is
63/√40 |
| |
|
|
En nu terug naar de bissectrice. |
| |
|
Voor de punten op de bissectrice
moet nu gelden dat de afstand tot het ene been van de hoek gelijk moet
zijn aan de afstand tot het andere been. Als de benen van de hoek de
lijnen k en l zijn, dan moet dus gelden: d(P,
l) = d(P, k), en voor die afstanden kunnen we de
hierboven gevonden formule gebruiken.
Kijk uit met die absolute waarden; bedenk dat
|x| = |y| betekent
x = y óf x = -y
Voorbeeld
2. Gegeven
zijn de lijnen 7x + 24y = 10 en 3x
- 4y = 8. Geef een vergelijking van de bissectrice. |
|
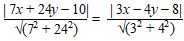 |
Daaruit
volgt 25 • |8
- 3x + 4y|
= 5 • |10 -
7x - 24y|
Vanwege de absolute waarde zijn er twee oplossingen:
25 • (8 - 3x + 4y) = 5
• (10 - 7x
- 24y)
of 25 • (8
- 3x
+ 4y) = -5 • (10 - 7x
- 24y)
Dat geeft na haakjes wegwerken als bissectrices de lijnen 4x
- 22y = 15 en 11x + 2y = 25 |
| |
|
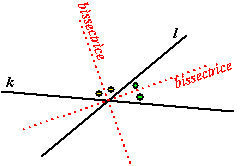
In de figuur hiernaast zie je dat er
inderdaad bij twee gegeven lijnen ook twee bissectrices zijn.
Dat klopt dus mooi met onze formule. |
 |
| |
|
| (Als we het in de volgende
opgaven hebben over de bissectrice van een hoek van een driehoek, dan
bedoelen we daarmee de bissectrice die binnen de driehoek ligt). |
| |
|
|
|
Het kan ook met een
vectorvoorstelling!
-en eigenlijk nog veel simpeler ook- |
| |
|
|
|
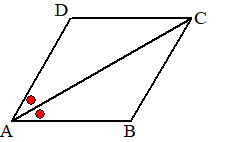
Met behulp van een
vectorvoorstelling kun je ook heel makkelijk een bissectrice opstellen.
Dat zit hem allemaal in de ruit hiernaast!
Omdat de driehoeken ACD en ACB congruent zijn (3 zijden gelijk) zijn ook
de rode hoeken gelijk, dus is diagonaal AC de bissectrice van AB
en AD.Maar voor de vectoren geldt: AC = AB + BC
Neem voor AB en AD de richtingsvectoren van de lijnen, en hun som is de
richtingsvector van de bissectrice! Simpel!! |
 |
| |
|
|
|
Je moet op één ding letten, en
dat is dat de richtingsvectoren wel even lang zijn, maar door ze met
geschikte getallen te vermenigvuldigen moet dat voor elkaar te krijgen
zijn natuurlijk.
Voorbeeld 2 nogmaals.
Gegeven zijn de lijnen 7x + 24y = 10 en 3x
- 4y = 8. Geef een vergelijking van de bissectrice. |
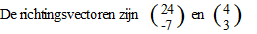 |
Die hebben lengte 25 en 5
dus als we die tweede nou vijf keer nemen zijn ze even lang.
Tel ze bij elkaar op om de richtingsvector van de bissectrice te vinden: |
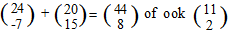 |
De vergelijking van de
bissectrice wordt dan 2x - 11y = c en
omdat het snijpunt (2.32, -0.26) van de lijnen daar op moet liggen geldt
2x - 11y = 7,5 ofwel 4x
- 22y = 15.
Dat is inderdaad één van de eerder gevonden bissectrices. Gelukkig maar. |
| |
|
|
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Geef de vergelijking van de bissectrices van de
volgende paren lijnen: |
| |
|
|
|
| |
a. |
5x - 12y = 4 en
4x + 3y = 8 |
|
| |
|
|
|
27x + 99y = 84 en -77x + 21y
= -124 |
|
| |
b. |
3x - 2y = 12 en 2x
+ 3y = -3 |
|
| |
|
|
|
5x + y = 9 en -x + 5y
= -15 |
|
| |
|
|
|
| 2. |
Gegeven zijn de evenwijdige lijnen
6x + 8y = 30 en 3x + 4y
= -10 |
| |
|
|
|
| |
a. |
Bereken de afstand tussen deze twee lijnen |
|
| |
|
|
|
| |
b. |
Stel een vergelijking op van de lijn
die evenwijdig is aan beide lijnen en er midden tussenin ligt.
Zo'n lijn heet een middenparallel en is dus de
conflictlijn van twee evenwijdige lijnen. |
| |
|
|
|
| 3. |
Een bekende wiskundige stelling zegt
dat de drie bissectrices van een driehoek door één punt gaan.
Bereken voor de driehoek ABC met A(1,2) en B(9,-6) en
C(4,6) de coördinaten van dat punt. |
| |
|
|
|
| 4. |
Gegeven is driehoek PQR met
P(1,2) en Q(5,5) en R(6,14)
Bereken het snijpunt van de bissectrice vanuit P met de
hoogtelijn vanuit Q. |
| |
|
|
|
| |
|
|
|
| 5. |
Gegeven is de lijn l:
10x + 24y = 50
Geef een vergelijking van de lijnen m en n
die evenwijdig zijn aan l en afstand 41/2
tot l hebben. |
| |
|
|
|
10x + 24y = 167
10x + 24y = -67 |
|
| |
|
|
|
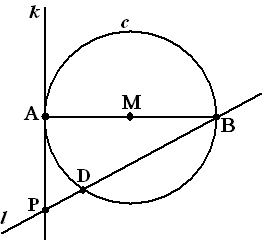
| 6. |
Gegeven is de cirkel c
met middellijn AB en middelpunt M. Lijn k raakt c in A.
Lijn l is een lijn door B die c in nog een ander punt D
(ongelijk aan A) snijdt. P is het snijpunt van k en l. Zie
de figuur hiernaast.
Er zijn twee cirkels die l raken en bovendien cirkel c
in A raken.
Teken in de figuur de twee
middelpunten van deze twee cirkels. Licht je werkwijze toe. |
 |
| |
|
|
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|