 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
Bernouilli-differentiaalvergelijkingen. |
| |
|
|
|
Die differentiaalvergelijkingen
uit de vorige les van eerste orde en tweede graad, met die
"wonderbaarlijke" substitutie-oplossing y = 1/u
waren eigenlijk niets meer dan een speciaal geval van de vergelijkingen
die we deze les zullen bespreken.
Het gaat vandaag om Bernouilli-differentiaalvergelijkingen, en die zien
er in het algemeen zó uit: |
| |
|
|
|
| dy/dx
= P(x) y + Q(x)
yn |
|
| |
|
|
|
De vorige les gold dat n =
2 en dat P(x) en Q(x) constant waren
(A en B). Nu niet meer....
De oplossing gaat in twee stappen: |
| |
|
|
|
|
stap 1: deel alles door yn
stap 2: substitueer u = y1
- n |
|
| |
|
|
|
Kijk maar waar dat toe leidt:
stap 1: dy/dx y -n
= P(x) y1 - n + Q(x)
stap 2: |
| |
u = y1 - n ⇒
u' = (1 - n) y' ⇒
y' y = 1/(1 - n) u' |
|
| |
Dan wordt de
differentiaalvergelijking uit stap 1: 1/(1-n)
u' = P(x) u + Q(x) |
| |
|
|
|
| En dat is weer een
lineaire eerste orde differentiaalvergelijking. Die kunnen we al lang
oplossen. Makkie! |
| |
|
|
|
Voorbeeld.
Los op: 2y' - 1/x y = x2y3
met y(1) = 1
stap 1: delen door y3 geeft 2y'
y -3 - 1/x
y -2 = x2
stap 2: u = y1-3 = y -2
dus u' = -2y -3 y'
en dat geeft dan bij stap 1: -2u' -
1/x
u = x2 ofwel u' +
1/2x
u = -1/2x2
|
De integrerende
factor is h = ò(1/2x)dx
= 1/2lnx
De algemene oplossing is dan: |
|
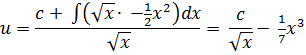 |
|
| |
|
|
|
| |
|
|
|
|
|
OPGAVEN |
| |
|
|
|
|
| 1. |
Los de volgende differentiaalvergelijkingen op: |
| |
|
|
|
|
| |
a. |
y' = y + e-x
y -2 met y(0) = 2 |
| |
|
|
|
|
| |
b. |
y'
-
3y = xy3 met y(0) =
6 |
| |
|
|
|
|
| |
c. |
y' + xy = xy2
met y(0) = 3 |
| |
|
|
|
|
|
 |
d. |
y' + xy = x3y3
met y(0) = 1 |
| |
|
|
|
|
| |
e. |
y' - y = xy5
(algemene oplossing). |
| |
|
|
|
|
| |
f. |
y' + 2xy + xy4
= 0 (algemene oplossing). |
| |
|
|
|
|
| |
g. |
yy' - xy2 +
x = 0 (algemene oplossing). |
| |
|
|
|
|
| 2. |
Van een touw van l m lang ligt 80 cm opgerold
aan de rand van een muur, de overige 20 cm hangt over de
muur naar beneden.
Vanaf het tijdstip t = 0 zakt het touw geleidelijk naar beneden onder invloed van de zwaartekracht
op het vrij hangende deel. Verwaarloos alle wrijving.
Dan geldt dv/dx
+ 1/x v = g/v
(v is de snelheid, x de lengte van het
loshangende stuk touw, g de
zwaartekrachtsversnelling))
|
| |
|
|
|
|
| |
a. |
Toon dat aan. |
| |
|
|
|
|
| |
b. |
Wat is de valsnelheid
van het touw op het moment dat het nét helemaal los is van
de muur? |
| |
|
|
|
|
| |
|
|
|
|
| 3. |
Geef de algemene oplossing van
(x/y - x3cosy)
y' = 2 |
| |
|
|
|
|
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|