asinx + bcosx = c


a sinx + b cosx = c	© h.hofstede (h.hofstede@hogeland.nl)

Dit is één van de weinige vergelijkingen die we nog niet direct algebraïsch aankunnen....
Maar via een omweg kan het toch.

We gaan proberen asinx + bcosx te herschrijven.
Haal eerst a buiten haakjes, dat geeft a(sinx + ^b/_a • cosx)
Stel nou, dat we een getal Φ kunnen vinden zodat tanΦ = ^b/_a(omdat tanf alle waarden kan aannemen, zal dat trouwens altijd lukken, dus dat stel kunnen we wel weglaten)
Dan staat er: a (sinx + tanΦ • cosx)

Maar daar in de teller staat een oude bekende: het is de formule voor sin(x + Φ) uit deze les.

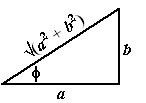
Dat volgt uit de figuur hiernaast, en daarmee kunnen we die cosΦ uit de noemer vervangen. Dat geeft:

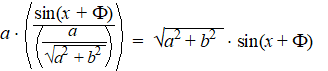En daarmee is de formule gevonden waarmee de vergelijking wél opgelost kan worden:

En als b negatief is, dan gaat het precies zo, maar krijg je aan de rechterkant sin(x - Φ) in plaats van sin(x + Φ)
Als a negatief is, zou ik eerst een minteken buiten haakjes zetten. Ook dan krijg je er weer zo eentje als hierboven.

Voorbeeld: Los op in [0, 2π]: 2sinx + 3cosx = 1. Geef je antwoord in twee decimalen.
2sinx + 3cosx = √(2² + 3²)sin(x + Φ) met tanΦ = ³/₂ dus Φ = 0,983
Dat geeft √13sin(x + 0,983) = 1 ⇒ sin(x + 0,983) = ¹/_√₁₃ = 0,277
⇒ x + 0,983 = 0,281 + k • 2π ∨ x + 0,983 = π - 0,281 + k • 2π
⇒ x = 5,58 ∨ x = 1,88

Voorbeeld. Los op in [0, 2π]: -4sinx + 2cosx = 3. Geef je antwoord in twee decimalen.
-4sinx + 2cosx = -(4sinx - 2cosx) = -√(4² + 2²)sin(x - Φ) met tanΦ = ²/₄ dus Φ = 0,464
Dat geeft -√20sin(x - 0,464) = 3 ⇒ sin(x - 0,464) = -³/_√20 = -0,671
⇒ x - 0,464 = -0,735 + k • 2π ∨ x - 0,464 = π - - 0,735 + k • 2π
⇒ x = 6,01 ∨ x = 4,34

OPGAVEN

Los algebraïsch op in [0, 2π]. Geef je antwoord in twee decimalen:

sinx + cosx = 0,5

1,99 en 5,86

4sinx - cosx = 2

0,75 en 2,88

4sinx + 3cosx = 3

0 en 1,85

sinx - 5cosx = -4

0,47 en 5,42

6sinx + 2cosx = -5

3,73 en 5,05

-2sinx + 5cosx = 3

0,60 en 4,92

Los algebraïsch op in [0, 2p]. Geef je antwoorden exact.

√3sinx - cosx = 1

π en ¹/₃π

sinx + √3cosx = -√3

π en 1¹/₃π

Voor welke waarde(n) van a hebben de volgende vergelijkingen géén oplossingen?

3sinx + 2cosx = a

a > √13 en a < -√13

asinx - 5cosx = 8

-√39 < a < √39

Gegeven is de functie f(x) = 3sinx - cosx in [0, 2π]

Bereken algebraïsch de nulpunten van f in twee decimalen nauwkeurig.

0,32 en 3,46

Voor welke waarden van x is de helling van de grafiek van f gelijk aan 1?
Geef een algebraïsche berekening en je antwoord in twee decimalen nauwkeurig.

(1.57, 3) en (5.36, -3)

Gegeven is de functie f(x) = psinx + cosx in [0, 2π]

Bereken a als deze vergelijking te schrijven is als f(x) = asin(x + ¹/₃π)

√(⁴/₃)

Bereken a als deze grafiek de grafiek van y = asin3x raakt in x = ¹/₆π.

²/₃√3

Los algebraïsch op in [0, 2p]:

geef je antwoord in 2 decimalen.

1.36 en 5.68

Bewijs dat de functie f(x) = 3sinx + 2cosx + 4 voor iedere x positief is.

Voor welke waarden van p heeft de vergelijking 6sinx + 8cosx = p geen oplossingen?

examenvraagstuk VWO, 1983.

V is de verzameling differentieerbare functies f van 〈0, π〉 naar R met de eigenschap dat voor elke x uit het domein geldt: f ' (x) = f(x) + 7cosx + sinx

Voor welke a ∈ R en b ∈ R geldt: de functie x → acosx + bsinx is een element van V?

De grafiek van een element van V raakt de grafiek van de functie x → e^x .
Bereken in twee decimalen nauwkeurig de coördinaten van het raakpunt.

(1.71, 5.54)

De grafiek van een element van V heeft een buigpunt op de lijn y = 10
Bereken de richtingscoëfficiënt van de raaklijn aan die grafiek in dit buigpunt.

16,2

Harmonische Trillingen.

Nu zijn we eindelijk in staat om te bewijzen dat de som van twee harmonische trillingen (= sinusgrafieken) met dezelfde frequentie altijd weer een harmonische trilling is met dezelfde frequentie. De fase en amplitude van beide trillingen mogen best verschillend zijn.

Neem f(x) = a • sinb(x - c) en g(x) = d • sinb(x - e) (de b's moeten gelijk zijn want die bepalen de periode/frequentie)
Omdat sin(a - b) = sinacosb - cosasinb geeft dat:
f(x) = a(sinbxcosbc - cosbxsinbc) en g(x) = d(sinbxcosbe - cosbxsinbe)
Optellen en groeperen geeft dan f + g = sinbx(acosbc + dcosbe) - cosbx(asinbc + dsinbe)
Maar daarin zijn (acosbc + dcosbe) en (asinbc + dsinbe) constanten. Noem ze bijvoorbeeld P en Q.
Er staat dus eigenlijk f + g = Psinbx - Qcosbx en dat is volgens bovenstaande theorie weer een gewone sinusfunctie.

Twee harmonische trillingen met dezelfde periode geven altijd weer een harmonische trilling

10.

Een punt beschrijft twee harmonische trillingen tegelijk.
De eerste trilling heeft amplitude 5 en de tweede amplitude 3.
De eerste trilling heeft loopt ¹/₆ periode op de tweede achter.
De periode van beide trillingen is 0,01 (dus de frequentie is 100)

Bereken de amplitude en de fase van de resulterende trilling.

√34 en 0,16