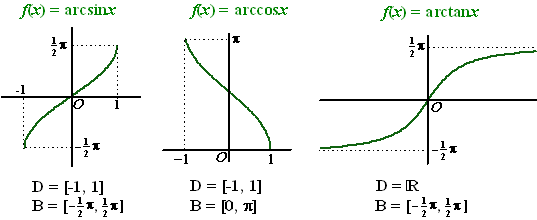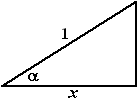Cyclometrische functies.

© h.hofstede (h.hofstede@hogeland.nl)
     

voorkennis:
inverse functies
Klinkt interessant en ook ingewikkeld, maar eigenlijk ken je die al!
De cyclometriche functies zijn de inversen van sinx en cosx en tanx. Dat zijn dus de functies die sinx en cosx en tanx "opheffen".
Je kent ze uiteraard ook al als de knoppen van je rekenmachine sin-1x en cos-1x en tan-1x. Die kon je gebruiken om bijvoorbeeld bij een gegeven sinx de hoek x te vinden.
 
Taalprobleem.

Nou is dat sin-1x  en cos-1x en tan-1x echt rekenmachine-taal. De functies hebben namelijk helemaal niets te maken met "tot-de-macht-min-één".
Immers dan zou het zijn  1/sinx enz.

Daarom is het beter om ze een andere naam te geven, en dat doen we door er "arc" voor te zetten:
 

arcsinx is de inverse van sinx
arccosx is de inverse van cosx
arctanx is de inverse van tanx
 
 
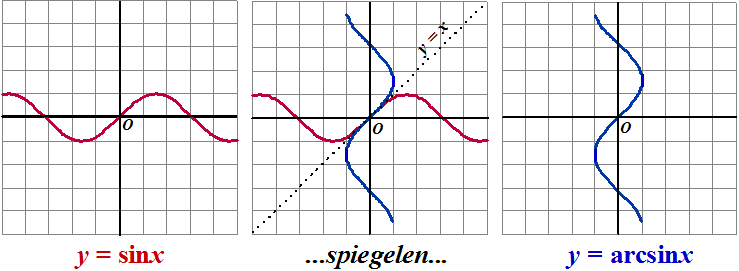
f(x) = arcsinx
       
Bij het maken van die "arc-functies" kom je één vrij groot probleem tegen, en dat zie je het best als je de grafieken ervan bekijkt.

Zoals je hopelijk nog weet vind je de grafiek van een inverse functie door de grafiek van de functie zelf te spiegelen in de lijn y = x. Dat is hieronder gebeurd voor de grafiek van f = sinx
       

       
Dat zou de blauwe grafiek van y = arcsinx opleveren.
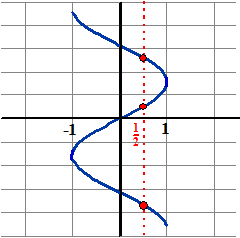
Maar dat geeft problemen........
Kijk maar naar de figuur hiernaast. Je ziet daar dat er bijvoorbeeld bij   x = 1/2 ineens oneindig veel y-waarden uitkomen.
En dat wist je natuurlijk ook al, want sinx = 1/2 levert de oplossingen
 x = 1/6π, 5/6π, 21/6π, 25/6π, enz. 

En dat willen we niet.
We willen graag dat een functie een apparaat is waar je één x in stopt, en waar dan hoogstens één y uitkomt (zodat je het kunt hebben over "de functiewaarde bij x = 0,5"  of   "de helling bij x = 0,2" en zo)
Om toch aan dit idee van een functie vast te kunnen houden, kun je daarom maar een deel van de blauwe grafiek hiernaast gebruiken. En dat moet dan een deel zijn waar er bij zo'n rode verticale lijn nooit twee snijpunten zijn met de grafiek.

       
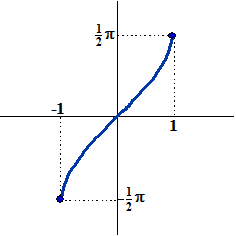
Er is gekozen voor het deel hiernaast. Lijkt me ook wel een vrij logisch keuze.

Dat betekent dat van de functie f(x) = arcsinx het domein gelijk is aan [-1, 1]  en het bereik  [-1/2π, 1/2π].

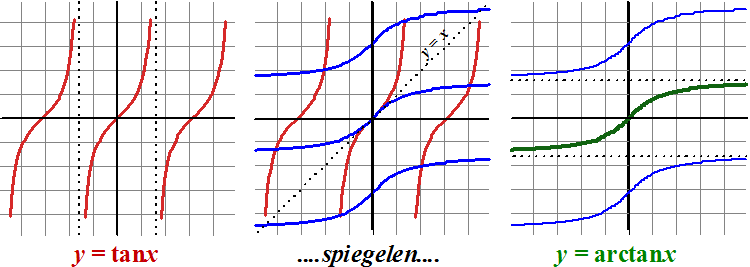
Dat betekent dus ook, dat als je de sin-1x knop van je rekenmachine gebruikt, je altijd een waarde tussen   -1/2π en 1/2π krijgt  (met graden is dat tussen -90° en 90°), en dat je zélf moet bedenken dat er nog veel meer mogelijke oplossingen zijn. (Misschien herinner je je nog dat we vroeger, bij de sinusregel, waar je steeds goed zélf moesten opletten of de hoek niet stomp was?) En ook die stomme "tweede oplossing" en dat "+k2π" bij sinusvergelijkingen zijn daar een gevolg van.

       
f(x) = arccosx  en  f(x) = arctanx
       
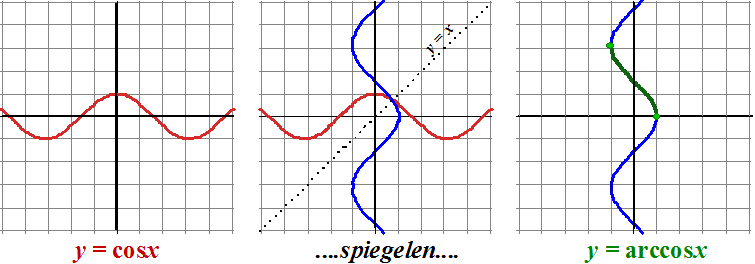
Deze functies ontstaan precies zo als die van arcsinx. Elke keer moet er gekozen worden welk deel van de grafiek we  nemen omdat bij elke x maar één y mag horen.
Hieronder zie je hoe dat in z'n werk is gegaan, en in de laatste grafiek rechts is aangegeven welk deel gekozen is (het groene deel).
       
       

       
Samengevat....
       
Hieronder zie je nog een keer de afspraken over de functies arcsinx en arccosx en arctanx
Bij elke grafiek staat vermeld wat het domein en wat het bereik is.
       

       
Vergelijkingen met deze functies.

De meeste directe vergelijkingen zijn vrij eenvoudig door te bedenken dat deze functies de inversen van de gewone sinx en cosx en tanx zijn.
Als je bijvoorbeeld moet oplossen  2 • arcsin(x - 1) = 1/2π dan gaat dat gewoon zó:

2 • arcsin(x - 1) = 1/2π  ⇒  arcsin(x - 1) = 1/4π ⇒  x - 1 = sin(1/4π) = 1/2√2 ⇒  x = 1/2√2 + 1
Je moet alleen even controleren of die 1/4π wel in het bereik van arcsinx zit. Als dat niet zo is, dan heeft de vergelijking geen oplossing, zoals in het volgende geval (oeps, nou heb ik alles al weer verraden):

arccos(2x) - π = 1/2π  ⇒  arccos(2x) = 11/2π  en dat kan niet want 11/2π  valt buiten het bereik van de arccosx functie (alhoewel cos11/2π  natuurlijk wel gewoon bestaat...)

Combinaties.

Leuker wordt het als we deze drie nieuwe functies gaan combineren met de oude drie gonio-functies!
Kijk, sin(arcsinx) is natuurlijk saai, want dat is gewoon x.
Maar hoe zit het met  cos(arcsinx) of  arctan(cosx)  of  tan(arccosx) .....................?
       
Bij zulke gevallen kun je het beste gewoon een sos-cas-toa-driehoekje tekenen.

Neem bijvoorbeeld  sin(arccosx)
Als je arccosx nou even α noemt, dan is dus cosα = x = x/1
Waarom schrijf ik daar nou weer ineens x/1 achter?
Nou, dan kun je dat tekenen  in een driehoekje met hoek α en aanliggende zijde x en schuine zijde 1, zoals hiernaast.

Dan is die andere rechthoekszijde (met Pythagoras) gelijk aan   √(1 - x2), dus is sinα = √(1 - x2)
Maar α was arccosx, dus is sin(arccosx) = √(1 - x2)
       
             
1. Bereken zonder je GR te gebruiken:
             
  a. arctan(√3)

1/3π
d. arcsin(tan1/4π)

1/2π
             
  b. arccos(-1/2)

2/3π
e. tan(arcsin1/2)

1/3√3
             
  c. arcsin(sin12/3π)

-1/3π
f. arccos(cos31/6π)

5/6π
             
2. Herleid:
             
  a. sin(arctanx)

x/√(1 + x2)
c. cos(arcsin2x)

√(1 - 4x2)
             
  b. tan(arccosx)

√(1-x²)/x
d. sin(2arctanx)

2x/(1+x2)
             
3. a. Leg duidelijk uit hoe de grafiek van sin(arcsinx) eruit zal zien. Denk om het domein en het bereik.
             
  b. Leg duidelijk uit hoe de grafiek van arcsin(sinx) eruit zal zien. Denk om het domein en het bereik.
             
4. Als je de grafiek van arcsinx spiegelt in de x-as en daarna 1/2p omhoog schuift krijg je de grafiek van arccosx.
Welk verband tussen arcsinx en arccosx volgt daaruit?
             
5. Los algebraïsch op:
             
  a. π + 2arcsin(2x) = 1/2π
           

-1/4√2
  b. 3arctan(x - √3) = 2π  
           

geen opl
  c. 1/3π + 2arccos(√x) = π  
           

1/4
             
6. We willen graag berekenen hoe groot  arcsin(cosx) is.
Als je dat getal even p noemt, dan geldt dus  sinp = cosx
Wat volgt daaruit voor  arcsin(cosx)?
           

1/2π - x
   
7. Los op:  arccosx = arctanx
           

x = √(-1/2 ± 1/2√5)
             
8. Gegeven zijn de volgende twee vergelijkingen:    cosy + xsiny = 2  en   xcosy + siny = x

Schrijf y als functie van x
           

y = arcsin(x/(1 - x)2)
             

© h.hofstede (h.hofstede@hogeland.nl)