| |
 |
| De
afgeleide functie. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
|
Een
opdracht.... |
|
|
| a. |
Bereken de helling van de grafiek van y
= 0,2x3 + 4x in het punt waar x
= 1 |
| b. |
Bereken de helling van de grafiek van y
= 0,2x3 + 4x in de punten waar x =
-3, -2, -1, 0, 2, 3 en vul de volgende tabel in. |
|
|
|
| x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
| helling |
|
|
|
|
|
|
|
|
|
|
|
c. |
Teken een grafiek met de punten
van deze tabel.
Op de y-as staat dus nu de helling van de grafiek
van y = 0,2x3 + 4x |
|
|
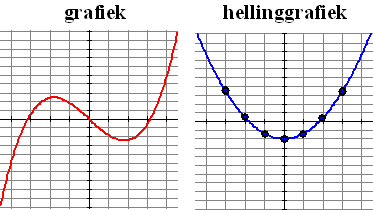
De grafiek die je zojuist getekend
hebt heet de hellinggrafiek van de grafiek van f.
Hopelijk heb je zoiets als hieronder gevonden: |
|
|
|
|
|
|
We gaan eens bekijken hoe je de
vorm van die hellinggrafiek kunt afleiden uit de vorm van de grafiek van
f zélf.
Een paar dingen zul je hopelijk logisch vinden.... |
|
|
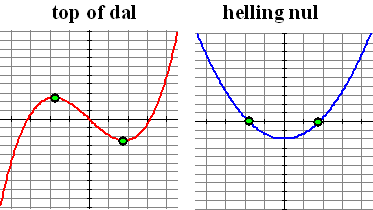
| 1.
Waar de grafiek van f een top heeft, snijdt zijn hellinggrafiek
de x-as. |
| |
|
|
Immers in een top (of dal natuurlijk) van een
grafiek is de helling nul (de raaklijn loopt horizontaal). Dus is de y
van de hellinggrafiek nul, dus ligt de hellinggrafiek op de x-as.
De volgende groene punten "horen bij elkaar". |
|
|
|
|
|
|
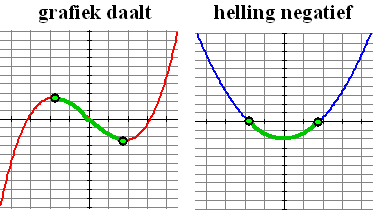
| 2.
Waar de grafiek van f daalt, ligt zijn hellinggrafiek onder
de x-as. |
| |
|
|
Immers als de grafiek daalt is de helling
negatief, dus is de y van de hellinggrafiek negatief, dus ligt de
hellinggrafiek onder de x-as. |
|
|
|
|
|
|
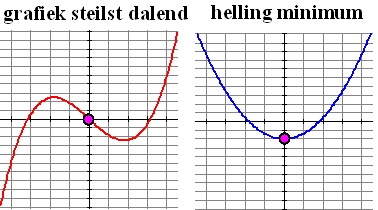
| 3. Waar
de grafiek van f het steilst daalt, heeft zijn
hellinggrafiek een minimum. |
| |
|
|
Immers, als de grafiek daalt is de helling
negatief, en als hij met meest daalt is de helling het meest negatief.
Dat moet dan wel een minimum zijn (en we weten ook dat dat minimum onder
de x-as zal zitten) |
|
|
|
|
|
|
Andere
namen...
Er zijn nog twee andere namen voor de hellingfunctie die bij een functie
f hoort, namelijk "afgeleide" en f
' (spreek uit: f-accent)
|
|
|
hellingfunctie
= afgeleide = f ' |
|
|
|
|
|
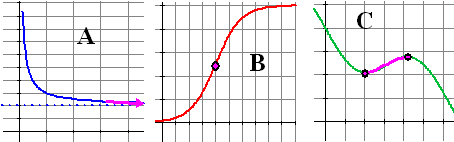
| 1. |
Hieronder staan drie
grafieken van functies f. Leg duidelijk uit wat de
paarse stippen of paarse delen van de grafiek van f
betekenen voor de grafiek van de afgeleide, f '. |
|
|
|
|
|
|
|
|
|
|
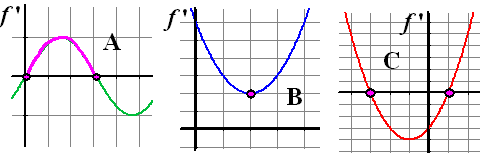
| 2. |
Hieronder staan drie
grafieken van hellingfuncties f ' . Leg duidelijk
uit wat de paarse stippen of paarse delen van de hellinggrafiek
betekenen voor de grafiek van f . |
|
|
|
|
|
|
|
|
|
|
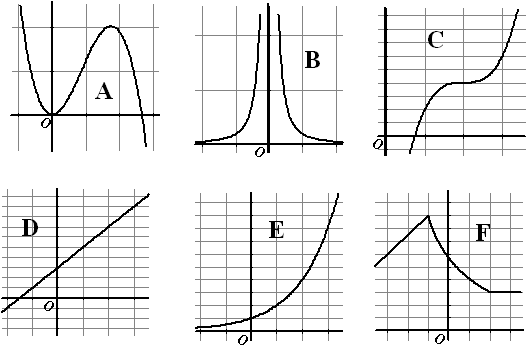
| 3. |
Schets van de grafieken hieronder de
bijbehorende hellinggrafiek. |
|
|
|
|
|
|
|
|
|
|
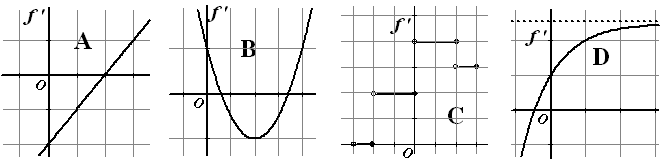
| 4. |
Schets van de
hellinggrafieken hieronder een mogelijke bijbehorende
grafiek van de functie zélf.
Leg uit waarom er meerdere mogelijkheden zijn. Wat hebben die
verschillende mogelijkheden met elkaar te maken? |
|
|
|
|
|
|
|
|
|
|
| 5. |
a. |
Wat betekent het voor de grafiek van
een functie f als de grafiek van zijn
hellingfunctie de x-as raakt? |
| |
|
|
|
b. |
Wat betekent het voor de
grafiek van een functie f als de grafiek van zijn
hellingfunctie een horizontale asymptoot heeft? |
| |
|
|
| |
c. |
Kun je een grafiek verzinnen die
gelijk is aan zijn eigen hellinggrafiek? |
| |
|
|
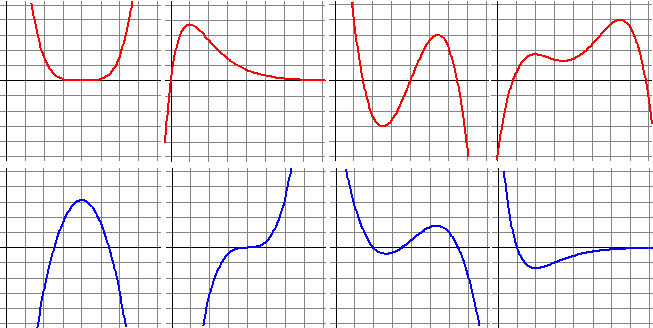
| 6. |
Van vier functies staat hieronder een rode grafiek.
Daaronder staan de bijbehorende vier afgeleide functies in het blauw en in
willekeurige volgorde.
Zoek bij elke functie de bijbehorende afgeleide.
Geef een duidelijke uitleg. |
| |
|
|
|
 |
| |
|
|
| |
|
|
|
|
|
|
|
| |
|
|
De afgeleide met de Grafische
Rekenmachine |
| |
|
De Grafische Rekenmachine heeft
een optie waarmee je direct de afgeleide functie kunt vinden.
Dat scheelt een boel werk!
Je vindt de optie bij
MATH
en dan nummer 8: nDeriv(
Het werkt als volgt: Zet de functie waarvan je de
afgeleide wilt berekenen in Y1.
Zet dan bij Y2: nDerive(Y1, X, X)
(Gebruik de dikke komma boven de 7, en die Y1 vind je bij VARS -
Yvars-Function, weet je nog?)
Dan is Y2 nu de afgeleide functie van Y1. |
| |
|
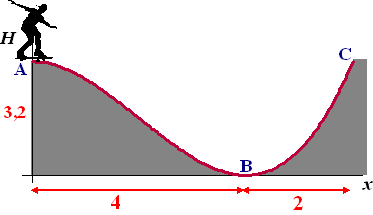
| 7. |
Om
sprongen en andere stunts met een skateboard te oefenen zijn in veel
parken skatebanen aangelegd. De meest gangbare vorm is de zogenaamde
"Halfpipe". Er zijn echter ook andere mogelijkheden. Hiernaast
is het zijaanzicht van een skatebaan getekend. Deze baan begint in punt
A op een hoogte van 3,2 meter en loopt daarna eerst af tot punt B op de
grond (4 meter horizontaal vanaf A). De baan gaat dan weer omhoog tot
een punt C op horizontale afstand 6 meter vanaf A. |
 |
| |
De formule die de vorm van de baan beschrijft is: H(x) = 0,1x3 - 0,6x2 +
3,2
Hierin is H de hoogte van de baan vanaf de grond gemeten en x
de horizontale afstand vanaf punt A, beiden in meters. |
| |
|
|
|
| |
a. |
Bewijs
dat de baan in de punten A en B inderdaad horizontaal loopt en bereken
vervolgens de hoogte van punt C. |
| |
|
|
|
| |
b. |
Tussen
A en B wordt de baan eerst steiler naar beneden en daarna weer vlakker.
Ergens tussen A en B ligt dus een punt waar de baan het steilst daalt.
Bereken de coördinaten van dat punt. |
| |
|
|
|
| 8. |
Het zuurstofgehalte van
de lucht is normaal gesproken gelijk aan 21%.
Maar als een grote groep mensen zich in een ruimte met
onvoldoende ventilatie bevindt, dan zal dat zuurstofgehalte
dalen.
Tijdens een erg lange vergadering van de ministerraad meet een
conciërge regelmatig het zuurstofgehalte in de vergaderruimte.
Op een gegeven moment vindt hij het onacceptabel laag geworden
en doet hij een boel ramen open.
Dan stijgt het zuurstofniveau gelukkig weer, zodat onze
ministers (voorzover ze daartoe in staat zijn) weer helder
kunnen nadenken.....
De conciërge stelt na afloop met zijn meetgegevens twee modellen
op; eentje voor het dalende zuurstofverloop (D) en eentje voor
het stijgende (S). Zijn metingen leveren op dat ongeveer geldt:
D(t) = 21 - 4t2 + t3
en S(t) = 21 - 12,56 • 0,9t
Daarin is t de tijd in uren |
| |
|
|
|
| |
a. |
Bepaal met je GR na
hoeveel tijd de conciërge de ramen openzette. |
| |
|
|
|
| |
b. |
Hoe snel daalde het zuurstofniveau
op t = 1? |
| |
|
|
|
| |
c. |
Op welk moment steeg het
zuurstofgehalte weer met 0,9 %/uur? |
| |
|
|
|
| |
|
| |
De conciërge merkt na afloop dat er
tussen t = 2 en het moment dat hij de ramen openzette
toch wel erg domme beslissingen zijn genomen. Hij besluit daarom
een soort alarmsysteem aan te leggen, dat waarschuwt als het
zuurstofgehalte in de ruimte te laag wordt.
Hij kan daarvoor kiezen uit twee verschillende systemen:
• Systeem I waarschuwt als het zuurstofgehalte onder de
19,5% komt.
• Systeem II waarschuwt als het zuurstofgehalte daalt met
meer dan 4% per uur |
| |
|
|
|
| |
d. |
Laat zien dat beide systemen met
bovenstaande functie D(t) ongeveer hetzelfde alarmmoment
opleveren. |
| |
|
|
|
 |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|
|
|