De afgeleide van gx

© h.hofstede (h.hofstede@hogeland.nl)

Terug naar de basis:
Ooit zijn we begonnen met de afgeleide in een punt door een punt vlak ernaast te nemen en dan tussen beide punten Δy/Δx uit te rekenen.  Als het punt  (x, f(x)) is, dan is het punt vlak ernaast  (x + dx, f(x + dx))
Dat geeft de volgende formule:

( dx nul nemen kan helaas niet want dan staat er 0/0))
Laten we dat gaan toepassen op f(x) = gx :
Waauw!! Wat een ontdekking.  Zie je het????
Het laatste stukje achter gx daar zit geen x meer in, dus dat is een constant getal! (hangt alleen nog van g af)
Neem bijvoorbeeld g = 2, dan is dat getal ongeveer  (20,0001 - 1) / (0,0001) = 0,693 dus de afgeleide is  2x • 0,693
Neem bijvoorbeeld g = 3, dan is dat getal ongeveer  (30,0001 - 1) / (0,0001) = 1,098 dus de afgeleide is  3x • 1,098
enz.
Zo heeft elke g zijn eigen constante getal.
Hiernaast staan voor een aantal g-waarden de bijbehorende waarden van dat constante getal.
Vroeger had je tabellenboeken om deze constante getallen voor allerlei g op te zoeken. maar tegenwoordig zijn die natuurlijk onder een knop van je rekenmachine gestopt.
Het is de knop  "ln".  Dus we schrijven:  constante getal = ln(g).
f(x) = gx  ⇒  f '(x) = gx • ln(g)
functie afgeleide
2x 2x • 0,693
3x 3x • 1,098
4x 4x • 1,386
5x 5x • 1,609
6x 6x • 1,792
enz. enz.
1. a. Gegeven is de functie  f(x) = 4 • 3x .  Benader de helling in het punt  (2, 36)
   

39,55
b. Gegeven is de functie  g(x) = 5 - 2x .  In welk punt is de helling ongeveer gelijk aan  -9 ?
   

3,699
c. Bereken het maximum van de grafiek van  y = 8x - 3x .
   

(1.81, 7.18)
d. Gegeven is de functie  h(x) = 2 - 0,5x .  Geef een vergelijking van de raaklijn in (-1, 0)
 

y = xln2 + 2ln2
2. Het is een vast gebruik geworden dat de eindexamenleerlingen een prachtig T-shirt ontwerpen als aandenken aan hun laatste schooljaar. Ook dit jaar koop ik het uiteraard, maar ik krijg er wel wat spijt van dat ik niet maat XXL, maar slechts maat L besteld heb. Het shirt blijkt namelijk nogal te krimpen bij het wassen.
Als ik dat door krijg houd ik een aantal wasbeurten de lengte angstvallig in de gaten:
lengte L (in cm) 46,4 44,1 41,9 39,8 37,8
na wasbeurt nr.: 5 6 7 8 9
Voor de lengte L als functie van de wasbeurt n blijkt te gelden  L(n) = 60 • 0,95n
a. Leg duidelijk uit hoe je dit verband uit bovenstaande tabel zelf ook zou kunnen afleiden.
b. Bij welke wasbeurt krimpt het shirt 0,4 cm? Bereken dit op twee manieren:
•  met behulp van de afgeleide van L(n)
•  algebraïsch met alleen de L(n) functie zelf.
   

n = 40
Denk om de kettingregel en al die anderen!
Natuurlijk blijven alle "oude" differentieerregels, zoals de productregel, de quotiëntregel en de kettingregel,  ook gelden.
De meest voorkomende regel bij afgeleiden met exponentiële functies is de kettingregel.
Dus denk erom:   23x - 4  moet je lezen als  2[  ]  dus de afgeleide is  2[  ] • ln2 • [  ]'  =  23x - 4 • ln2 • 3
  OPGAVEN
 
3. Geef de afgeleide functie van de onderstaande functies.
a. f(x) = 3 • 46-2x e. f(x) = √(x + 3x)
b. f(x) = 2x + 3√x f. f(x) = 5 - 12 • 0,54x - 2
c. f(x) = (2x + 3)4 g. f(x) = 4x + 52x
d. f(x) = x • 5x h.

 
4. 52x is hetzelfde als  25x
a. Bewijs dat dat inderdaad zo is.
b. Bewijs met de afgeleiden van deze functies dat moet gelden  ln25 = 2 • ln5.
c. Bewijs op dezelfde manier dat moet gelden  a • lng = ln ga .
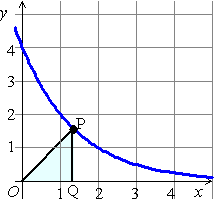
5. Hiernaast zie je de grafiek van y = 4 • 0,5x
Vanaf punt P is een loodlijn op de x-as neergelaten.
Dat geeft punt Q op de x-as, en driehoek OPQ.

Bereken voor welke P de oppervlakte van driehoek OPQ maximaal zal zijn. Geef een algebraïsche berekening, en geef de coördinaten van P in twee decimalen nauwkeurig.

   

(1.44, 1.47)
6. Een zonnebloem groeit zeer snel. De  lengte is 12 cm op t = 6, en al 350 cm op t = 14 waarbij t de tijd in weken na het zaaien is. 
         
  a. Stel een functievoorschrift voor de lengte op als de groei vanaf t = 6 lineair verloopt en bereken vervolgens daarmee de lengte van de zonnebloem op t = 12
       

265,5 cm
  b. Stel een functievoorschrift voor de lengte op als de groei vanaf t = 6 exponentieel verloopt en bereken vervolgens daarmee de lengte van de zonnebloem op t = 12
       

150,61 cm
  c. Bereken algebraïsch op welk tijdstip het lineaire groeimodel en het exponentiële groeimodel dezelfde groeisnelheid geven.
       

t = 11,03
         
7. Koolstof -14  (C-14) is een radioactieve stof. Dat houdt in dat C-14 straling uitzendt met een bepaalde activiteit A (eenheid 'Curie'). Deze activiteit neemt in de loop der jaren heel langzaam af. Metingen aan oude opgravingen hebben de grafiek  hiernaast (op enkellog-papier) opgeleverd.  Daarin is de tijd (t) in jaren gegeven en de activiteit (A) in Curie.

       
  a. Geef het functievoorschrift van A als functie van t (neem een groeifactor van 4 decimalen nauwkeurig)
     

A = 0,1 • 0,9988t
  Neem, als je de vorige vraag niet hebt beantwoord:  
A(t) = 0,2 . (0,9995)t
       
  b. Wanneer (in gehele jaren) was de activiteit van C-14 gelijk aan 480 milliCurie?
       

-6907 of -15198
  c. Bereken de halfwaardetijd van C-14 (dat is de tijd waarin de activiteit halveert).
       

577 of 1386
  d. Wanneer daalt de activiteit van C-14 met een snelheid van 0,02 milliCurie per jaar?
       

-4260 of -10593
         
8. Voor het aantal kakkerlakken (K, in duizenden) in een verlaten flatgebouw geldt bij benadering de volgende formule, waarin t de tijd in maanden is.
 

         
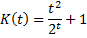  Bereken algebraïsch het maximale aantal kakkerlakken.
       

2127
         
9. In een regenton zit 1200 liter water. Je kunt de ton leeg laten stromen door een kraantje aan de onderkant open te zetten. Tijdens dat leegstromen geldt voor het aantal liters (L)  in de ton bij benadering de volgende formule:
         
 

         
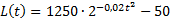  Daarin is t de tijd in minuten met t = 0 het moment van openzetten van het kraantje.
         
  a. Na hoeveel tijd zit er nog 500 liter in de ton?
       

7,696 min.
  b. Hoe snel (in liter per minuut) stroomt het water op t = 5 uit de ton?
       

122,5 l/min
  c. Op welk tijdstip is de uitstroomsnelheid maximaal? Geef een algebraïsche berekening.
       

t = 6
         
10. Een zware storm op de Zwarte Zee in november 2007  waarbij vijf vrachtschepen gezonken zijn was één van de grootste Russische ecologische rampen van de laatste jaren.  De meeste schepen kwamen in de problemen in de Straat van Kertsj, die de Zwarte Zee verbindt met de kleinere Azov-zee. Een Russische olietanker brak in tweeën en verloor een grote hoeveelheid stookolie in de buurt van de Oekraïense haven Kertsj.
Voor de hoeveelheid olie (H(t) in liters)  in de tanker gold het volgende model (met t de tijd in uren met t = 0 op het moment van zinken van de tanker):  H(t) = 40000 • 3-0,15t
         
  a. Bereken wanneer er nog de helft van de olie in het schip aanwezig zal zijn
       

t = 4,21
  b. Met welke snelheid (liters per minuut) stroomde de olie op t = 3 de zee in?
       

67 l/min
  Door het zware weer konden de oliebestrijdingsvaartuigen pas 5 uur na de ramp aanwezig zijn.
De bestrijdingsvaartuigen kunnen per uur 500 liter uit zee halen, dus voor de verwijderde hoeveelheid olie geldt de formule  V(t) =  500 • (t - 5)
         
  c. Bereken hoe groot de maximale hoeveelheid olie in zee zal zijn.
       

31641 liter
         
11. In 2003 waren er 8000 meisjes en 23000 jongens die VMBO-techniek deden.
Dankzij een intensieve reclamecampagne nam vanaf 2003 het aantal meisjes dat VMBO-techniek deed toe met 4,5% per jaar. Tegelijkertijd nam het aantal jongens dat VMBO-techniek deed af met 600 per jaar.
Neem aan dat deze groei en afname voorlopig zo door zullen gaan.
         
  a. In welk jaar zullen er dan voor het eerst meer meisjes dan jongens VMBO-techniek doen?
       

2017
  b. Toon aan dat het totaal aantal leerlingen in VMBO-techniek tussen 2007-2008 daalde.
         
  c. Bereken met behulp van een afgeleide in welk jaar de daling van het totaal aantal VMBO-techniek studenten zal worden omgebogen naar een stijging.
       

2015-2016
         
12. Het reclamebureau UNICOM heeft onderzoek verricht naar de advertenties voor tweedehands auto's in veel landelijke dagbladen. Men  wilde onderzoeken of er ook op deze tweedehands markt een vraag-en-aanbod principe van toepassing was. Daartoe telde men van 7 dagbladen hoeveel advertenties er in een heel jaar  voor tweedehands auto's in verschenen  en ook wat de gemiddelde verkoopprijs van deze auto's was. De volgende tabel was het resultaat:
   
 
aantal advertenties (A) 456 725 827 989 1297 1392 1697
gemiddelde prijs (P) 41,6 29,0 25,3 20,4 13,5 11,9 7,9
         
  Daarin is P in duizenden euro's. 
Het leek er op dat de gevonden prijs P bij benadering exponentieel afhankelijk was van het aantal advertenties A.
         
  a. Laat zien dat deze constatering juist is.
         
  Wanneer er van uit wordt gegaan dat er een exponentieel verband is tussen A en P en dat de grafiek door de punten (700,30) en (1600,9) gaat, kan de gemiddelde  prijs bij een aantal van 600 advertenties berekend worden.
         
  b. Bereken deze prijs in duizenden euro's nauwkeurig.
       

34
  In hun model namen de mensen van UNICOM de volgende formule voor  het verband tussen A en P aan:
P = 76 • 2-0,00193A
         
  c. Als alle geadverteerde auto's ook verkocht zouden worden, bij welk aantal advertenties in een krant is de "omzet" van die krant  (hoeveelheid geld die bij de adverteerders terechtkomt) dan het grootst?
       

748
   
   

© h.hofstede (h.hofstede@hogeland.nl)