 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
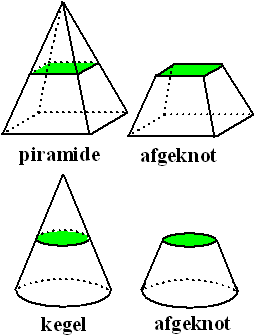
Afgeknotte Kegel en Piramide. |
|
|
Een afgeknot lichaam is een
ruimtelijke figuur waar stukken zijn afgesneden. In deze les
bekijken we twee soorten daarvan: de kegel en de piramide waarvan de top
is afgesneden door een vlak evenwijdig aan het grondvlak.
Hiernaast zie je dat. De piramide kan trouwens elk grondvlak hebben, het
hoeft niet per se vierkant te zijn zoals hiernaast.
De berekening van de inhouden van zulke afgeknotte piramides en
afgeknotte kegels gaan allemaal op dezelfde manier. En die manier gaat
in drie stappen:
| |
1. Bereken de inhoud van
de niet-afgeknotte figuur.
2. Bereken de inhoud van het deel dat eraf
wordt gesneden.
3. Trek die twee van elkaar af. |
|
| |
De moeilijkste stap is nummer 2. ......
|
 |
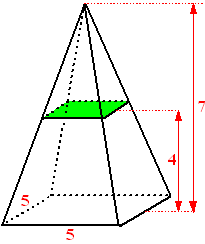
| Ik zal het voordoen met een
piramide (de kegel gaat precies zo). Laten we een piramide nemen met
vierkant grondvlak met zijden 5 bij 5 en hoogte 7. |
We snijden de top eraf op
hoogte 4 vanaf het grondvlak.
De inhoud van de hele piramide was 1/3
G
h = 1/3 25 7 = 581/3
Nu het eraf gesneden stuk. Het belangrijkste dat je moet zien is, dat de
piramide die er afgesneden is gelijkvormig is met de hele piramide (want
alle hoeken zijn gelijk). Dus geldt tussen die beide figuren een
verkleiningsfactor k. De afgesneden top heeft hoogte 3 en de
oorspronkelijke piramide had hoogte 7. Dat betekent dat die
verkleiningsfactor k gelijk is aan 3/7.
En nou komt het:
| |
|
Als voor de lengtes factor k
geldt,
Dan geldt voor de inhouden factor k3
|
|
| |
|
 |
In dit geval is de
verkleiningsfactor voor de inhouden dus gelijk aan (3/7)3
= 27/343
Dus de inhoud van de afgesneden top is gelijk aan
27/343
581/3
≈ 4,5918
Dan is de inhoud van de afgeknotte piramide gelijk aan 581/3
- 4,5918 ≈ 53,74 |
|
|
|
Als de hoogtes niet gegeven zijn. |
|
|
Dan wordt het iets lastiger.
Deze keer maar een kegel als voorbeeld. De afgeknotte kegel hiernaast
heeft hoogte 6, straal grondvlak 12 en straal bovenvlak 8.
De grote vraag is nu: Hoe hoog was de oorspronkelijke kegel?
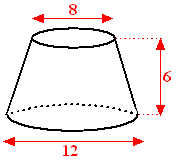
Om die vraag te beantwoorden teken je het vooraanzicht van de
oorspronkelijke kegel. Dat ziet er zó uit:
|
 |
|
|
Daarin kun je zien dat dat blauwe
driehoekje gelijkvormig is met driehoek TMA. Dus zijn de verhoudingen
van de zijden gelijk, dus geldt 4/x =
6/(6+x) . Vermenigvuldig met x
en met 6 + x en je hebt 4(6 + x) = 6x
Daaruit volgt 24 + 4x = 6x ⇒
x
= 12 dus de hoogte was
oorspronkelijk 6 + x = 6 + 12 = 18
Dan was de oorspronkelijke inhoud 1/3 π 62
18 = 216π
De verkleiningsfactor voor het topje is 12/18 =
2/3 dus de voor de inhoud is dat (2/3)3
= 8/27
Dus de inhoud van de toppiramide is 8/27
216π = 64π
Dan blijft voor de afgeknotte piramide over 216π - 64π
=
152π
(≈ 478). |
| |
|
| Het kan
ook zó: |
| |
|
Je kunt de hoogte van de oorspronkelijke
kegel ook als volgt beredeneren.
over een hoogte van 6 cm neemt de diameter af van 12 naar 8.
bij 6 cm hoogteverschil hoort dus 4 cm afname van de diameter
bij 12 cm afname van de diameter hoort dan 18 cm hoogteverschil
dus de oorspronkelijke hoogte was 18.
Als de getallen niet zo mooi uitkomen kun je er natuurlijk zo'n
verhoudingsschema voor maken: |
 |
| |
|
|
Δ hoogte |
6 |
?? |
|
Δ diameter |
4 |
12 |
|
|
| |
|
| |
|
|
OPGAVEN |
| |
|
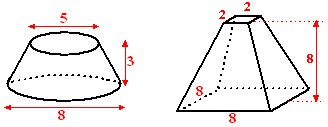
| 1. |
Bereken de inhoud van de volgende twee
afgeknotte figuren. |
| |
|
|
| |
 |
| |
|
| |
|
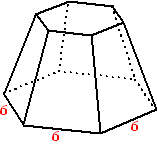
| 2. |
Hiernaast zie je een
afgeknot zeszijdig prisma. Het grondvlak is een regelmatige
zeshoek met zijden 6.
Het bovenvlak is een zeshoek met zijden 2.
De loodrechte afstand tussen bovenvlak en ondervlak is 10.
Bereken de inhoud in twee decimalen nauwkeurig. |
 |
| |
|
|
|
|
| |
|
|
|
|
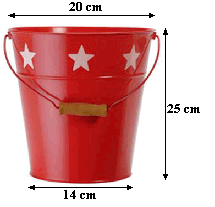
| 3. |
Hoeveel liter gaat er in het
speelgoedemmertje
hiernaast? |
 |
| |
|
|
|
|
| |
|
|
|
|
| 4. |
Hiernaast zie je een
originele klok.
Het is een piramide die verdeeld is in 4 stukken. De middelste
twee stukken draaien rond en geven zo de uren en minuten aan.
Aan de vorm van de piramide kun je dan zien hoe laat het is!!
(Of als je een watje bent, dan kijk je naar de schaalverdeling
op de middelste twee stukken)De vier stukken van de piramide
hebben hoogtes (van onder naar boven) gelijk aan 4, 3, 2 en 6 cm
Het grondvlak is een vierkant met zijden 12.
Bereken de inhoud van de vier afzonderlijke stukken. |
 |
| |
|
|
|
436,05
174,72
63,15
46,08 |
|
| |
|
|
|
|
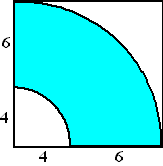
| 5. |
Hiernaast zie je in het
blauw de uitslag van de mantel (dat is het gekromde oppervlak)
van een afgeknotte kegel.
Bereken de inhoud van die afgeknotte kegel. Geef je antwoord in
één decimaal nauwkeurig. |
 |
| |
|
|
|
|
| |
|
|
|
|
 6. 6. |
Een slimme leerling moet van
een groot aantal afgeknotte kegels de inhoud berekenen. Zij
ontwikkelt daarom de volgende formule: I =
1/3πh
(R2 + rR + r2)
Daarbij is h de hoogte van de kegel en zijn R en r
de stralen van ondervlak en bovenvlak.
Toon aan dat deze formule juist is!!! |
| |
|
|
|
|
| 7. |
Het heerlijke toetje
hiernaast heeft een grondcirkel met straal 8 cm.
De bovencirkel heeft straal 6 cm.
Bereken de hoogte van het toetje als de inhoud gelijk is aan 850
cm3
|
 |
| |
|
|
|
|
| |
|
|
|
|
| 8. |
Een goudstaaf
heeft als grondvlak een rechthoek van 18 bij 7,2 cm en als
bovenvlak een rechthoek van 15 bij 6 cm.
De hoogte van de goudstaaf is 4 cm.
Goud heeft een soortelijk gewicht van 19,3 gram per cm3
. |
 |
| |
a. |
Toon aan dat deze goudstaaf de vorm
van een afgeknotte piramide heeft. |
| |
|
|
| |
b. |
Bereken het gewicht van deze
goudstaaf. |
| |
|
|
|
|
| |
|
|
|
|
 |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|