| |
 |
|
Absolute Waarde (deel 2) |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
 |
| |
|
|
absolute waarde (1) |
In de vorige les over absolute
waarde heb je (hopelijk) geleerd wat het eigenlijk is, en hoe je
eenvoudige vergelijkingen kunt oplossen en eenvoudige grafieken kunt
tekenen.
De hoofdregel die daar behandeld werd is eigenlijk: |
| |
|
|
|
|
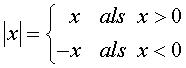 |
| |
|
|
|
In deze les zullen we wat
"spannender" gevallen bekijken, met steeds in ons achterhoofd deze
hoofdregel.
Het gaat dan vooral om de gevallen waarin dat stuk tussen die absolute
waarde strepen slechts een deel is van een groter vergelijking of
formule.
De algemeen oplossing voor zulke gevallen is: |
| |
|
|
|
|
|
|
|
Splits het stuk wat tussen die
strepen staat. Als het positief is, dan kun je de strepen gewoon
weglaten. Als het negatief is, dan kun je ze ook weglaten, maar dan moet
je het positief maken door er een extra minteken voor te zetten.
Voorbeeld: |
|
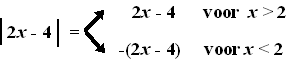 |
| |
|
|
|
Het resultaat van dat splitsen is
dat je twee "gewone" formules overhoudt zonder die vervelende
absolute-waarde-strepen.
Dat werkt ook bij ingewikkelder vergelijkingen, kijk maar: |
| |
|
|
|
| Voorbeeld. |
|
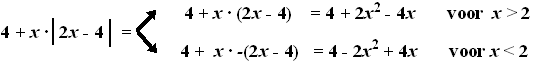 |
| |
|
|
|
| Nu zijn twee formules
overgebleven (4 + 2x2 - 4x en
4 - 2x2 + 4x) waar geen vervelende
absolute waarde meer in voorkomt. Bedenk wel dat de eerste formule
alleen geldig is voor x > 2 en de tweede alleen voor x <
2. |
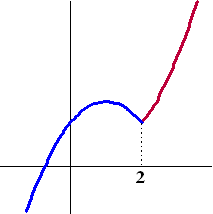
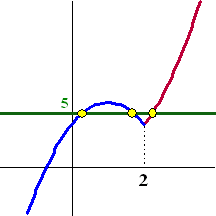
De grafiek van
y = 4 + x │2x
- 4│ ziet er bijvoorbeeld uit als
hiernaast.
Het zijn twee delen van parabolen.
de parabool y = 4 + 2x2
- 4x
voor x > 2 (de rode
parabool)
de parabool y = 4 - 2x2 + 4x
voor x < 2 (de blauwe
parabool)En voor
vergelijkingen gaat het natuurlijk precies zo!
Stel dat je moet oplossen 4 + x
│2x
- 4│
= 5
Dan geeft dat na het splitsen twee nieuwe vergelijkingen:
1: 4 + 2x2 - 4x = 5
voor x > 2
2: 4 - 2x2 + 4x = 5 voor
x < 2 |
 |
| |
|
|
|
| Die zijn apart
eenvoudig op te lossen. Bedenk wel dat je van de eerste vergelijking
alleen de oplossingen die groter dan 2 zijn mag nemen, en van de tweede
alleen de oplossingen die kleiner dan 2 zijn. |
De oplossingen van de eerste vergelijking zijn ongeveer 2,22 en -0,22 en
daar blijft alleen 2,22 van over. Vanwege de voorwaarde x >
2
De oplossingen van de tweede vergelijking zijn ongeveer 0,29 en 1,71 en
die zijn beide goed (kleiner dan 2)
De vergelijking heeft dus 3 oplossingen, zoals je hiernaast in de
grafiek inderdaad ziet.
Inderdaad twee snijpunten met de blauwe grafiek en eentje met de rode. |
 |
| |
|
|
|
|
Hoe zie je waar je moet splitsen? |
| |
|
|
|
Dat is erg eenvoudig:
de grensgevallen zijn de x-waarden waar "dat wat tussen de
absolute-waarde-strepen staat" nul is.
Dat kan soms wel op meerdere plekken zijn.
Voorbeeld. Los op x +
│x2
- 4│ = 1
Los eerst op x2
- 4
= 0 (alleen het stuk tussen de absolute-waarde-strepen).
Dat geeft x = 2 en x = -2
Voor x < -2 is het stuk tussen de strepen positief.
Voor -2 < x < 2 is het stuk tussen de strepen
negatief.
Voor x > 2 is het stuk tussen de strepen positief.
Daarom splitsen we als volgt: |
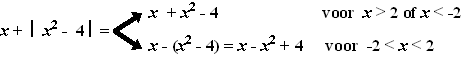 |
| |
dan hebben we twee
vergelijkingen over:
1. x + x2 - 4 = 1 voor
x > 2 of x < -2
2. x - x2 + 4 = 1 voor
-2 < x < - 2
De oplossing van de eerste vergelijking is x = 1,79 of
x = -2,79 en alleen die tweede is goed
De tweede vergelijking heeft oplossingen -1,30 en 2,30 en
alleen die eerste is goed.
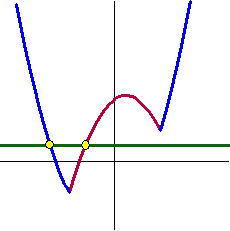
Dus heeft deze vergelijking twee oplossingen: x = -2,79
of x = -1,30.
Hiernaast zie je de grafiek met die oplossingen. |
 |
| |
|
|
|
|
Drie (of zelfs meer)
functievoorschtiften... |
|
| |
|
|
|
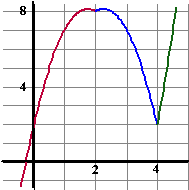
Neem bijvoorbeeld de
functie f(x) = │x
- 2│+ x │2x
- 8│
Je moet splitsen waar die stukken tussen de absolute-waarde-strepen nul
zijn. Dat is bij x = 2 en bij x = 4.
Daarom krijg je drie "gebieden": |
 |
| |
als x < 2 dan
zijn beide stukken tussen die strepen negatief, dus moet er, om de
strepen weg te halen, een extra min voor worden gezet.
Dat geeft f(x) = -(x - 2) + x -(2x
- 8) = -2x2 + 7x + 2 |
| |
als 2 < x < 4
dan is het eerste stuk positief, en het tweede negatief, dus alleen voor
het tweede moet een minteken komen.
Dat geeft f(x) = (x - 2) + x -(2x
- 8) = -2x2 + 9x
- 2 |
| |
als x > 4 is
alles positief en kunnen alle strepen weg.
Dat geeft f(x) = (x - 2) + x(2x
- 8) = 2x2
- 7x - 2 |
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Los op (rond indien nodig af op 2 decimalen): |
| |
|
|
|
| |
a. |
x │6
-
x │ = 5 |
|
| |
b. |
2x + x
│1 - x│ = 0 |
|
| |
c. |
│x
-
1│ = 2 │5
- x│ |
|
| |
|
|
|
| 2. |
Een leerling beweert:
│x
- a│ │x
-
b│ = │(x - a)(x
- b)│
Leg uit of dat klopt of niet. |
| |
|
|
|
| 3. |
Splits de volgende
functievoorschriften in voorschriften zonder
absolute-waarde-strepen. |
| |
|
|
|
| |
a. |
f (x) = 2│4
- 2x│
- 3│x + 4│ |
|
| |
b. |
g(x) = 2x
│x2 -
6x + 8│ |
|
| |
c. |
h(x) =
│x
- │2
- x││ |
|
| |
|
|
|
| 4. |
De
vergelijking | | x - 2 |
- 3 | = a heeft
precies drie verschillende oplossingen.
Wat is a ? |
| |
|
|
|
| |
|
|
|
| 5. |
Schets de grafiek
van f(x) = | -8 + | x |
| |
| |
|
|
|
| 6. |
examenvraagstuk 1981. |
| |
|
|
|
| |
De functie f van R
naar R is gegeven door: |
| |
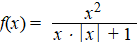 |
| |
|
|
|
| |
a. |
Los op: f(x) <
1/2x |
| |
|
|
|
| |
b. |
Onderzoek f en
teken de grafiek van f. |
| |
|
|
|
| 7. |
examenvraagstuk VWO Wiskunde B, 1991. Van R naar R is
gegeven de functie: |
| |
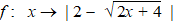 |
| |
|
|
|
| |
Ten opzichte van
een rechthoekig assenstelsel Oxy is K de grafiek van f.
Een lijn y
= a met a ∈ 〈 0,2 ]
snijdt K in de punten A en B.
Bewijs dat AB = 4a. |
| |
|
|
|
| 8. |
examenvraagstuk VWO,
1971
De functie f wordt gedefinieerd door: |
| |
f(x)
= |2x - 4|/(x
- 1) |
| |
|
|
|
| |
a. |
Teken in één figuur de grafieken van
f en g1 |
| |
|
|
|
| |
b. |
Voor welke p ∈ R
geldt: de grafiek van gp heeft geen punt
gemeen met die van f ? |
| |
|
|
|
| |
c. |
Voor welke p ∈ R
geldt: de grafiek van gp heeft één punt
gemeen met die van f ? |
| |
|
|
|
| |
d. |
Voor welke p ∈ R
geldt: de grafiek van gp heeft twee
punten gemeen met die van f ? |
| |
|
|
|
| |
e. |
Voor welke p ∈ R
geldt: de grafiek van gp heeft drie
punten gemeen met die van f ? |
| |
|
|
|
| |
f. |
Voor welke p ∈ R
geldt: de grafiek van gp heeft vier
punten gemeen met die van f ? |
| |
|
|
|
| 9. |
Examenopgave VWO wiskunde B, 2019-II De functie
f
wordt gegeven door
f
(x)
= |
x
-
2 |
(1/2x
+
2) + 1
De grafiek van
f
heeft een knik in het punt
A.
Dit punt verdeelt de grafiek in twee delen. De lijn
l
is de raaklijn in
A
aan het linkerdeel van de grafiek. Zie de
figuur. |
| |
|
|
|
| |
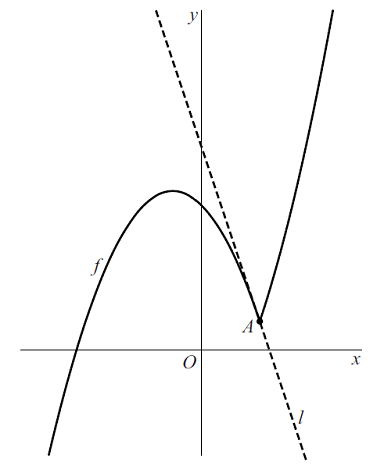 |
| |
Stel op exacte wijze een vergelijking van
lijn l
op. |
| |
|
|
|
| 10. |
De functie f is
gegeven door |
| |
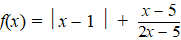 |
| |
|
|
|
| |
In de
figuur is de grafiek van f weergegeven. |
| |
|
|
|
| |
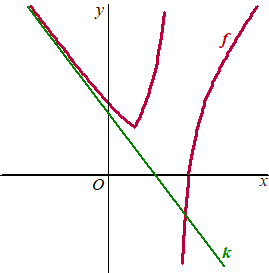 |
| |
|
|
|
| |
Bereken
exact voor welke waarden van x de grafiek van f
onder de x-as ligt |
| |
|
|
|
 |
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|