Absolute Waarde.

© h.hofstede (h.hofstede@hogeland.nl)

Soms wil je gewoon graag dat iets positief is. Normale mensen denken dan natuurlijk meteen aan het saldo op hun bankrekening, maar wiskundigen hebben vaak een andere kijk op de zaak. Die willen graag dat functies die bijvoorbeeld de afstand tussen twee punten of een oppervlakte een positief getal opleveren.
Om te zorgen dat iets positief wordt hebben ze daarom een aparte notatie verzonnen; twee verticale strepen ergens omheen maken het positief.
Voorbeelden:
| 3 | = 3
| -5 | = 5
| 2 - 6 | = 4
| 5 - 2 | = 3
In het algemeen geldt: 

 
(en als x gelijk is aan 0 dan is de absolute waarde ervan dat uiteraard ook)
GEVOLGEN VOOR VERGELIJKINGEN.
Voor eenvoudige vergelijkingen met absolute waarde erin moet je er steeds op bedacht zijn dat er twee mogelijke oplossingen zijn, namelijk positief en negatief.

Voorbeeld:      Los op:   | 2x - 10 | = 6 
Deze vergelijking heeft twee mogelijkheden, namelijk  2x - 10 = 6  of  2x - 10 = -6  (want in beide gevallen is het 6 als je het positief maakt)  Dat geeft dus oplossingen   x = 8  of  x = 2.
GEVOLGEN VOOR GRAFIEKEN.
Voor grafieken betekent het dat ze altijd positief zijn, dus boven de x-as. De stukken die onder de x-as zitten worden door zulke absolute-waarde strepen "omgeklapt". Bekijk de volgende paren grafieken maar:

1.  Los op:
a. | x + 3 | = 2
-1 of -5
e. 2 + | -2x + 1 | = 3
0 of 1
b. | 3x - 5 | = 7
-2/3 of 4
f. 5 - | 3 + 6x | = 2
0 of -1
c. | 5x + 1 | = 3
-4/5 of 2/5
g. 2 • | 7x + 2 | =  12
-8/7 of 4/7
d. | 1 - 3x | = 5
-4/3 of 2
h. 1 + 3 • | x + 4 | = 22
-11 of 3
2. Los op:
a. | x + 1 | = | 3 - 2x |
2/3 of 4
c. | x2 + 2x + 5 | = 8 
1 of -3
b. | 2x - 1 | = | x |
1/3 of 1
d. | x3 + 6 | =  80 
741/3 of (-86)1/3
3.  Schets de grafieken van:
a. y = | 2x - 4 |   d. y = 3 + 5 • | x + 2 |  
b. f(x) =  1 + | x - 4 |   e. f(x) = | x3 |  
c. y = 2 • | x - 6 |   f. f(x) =  | x2 + 2x - 3 |  
4. Twee veerboten varen op en neer tussen Harlingen en Vlieland. Ze varen volgens het zelfde traject. De afstand Vlieland-Harlingen is 17 mijl en dat is ongeveer 27,4 km.
Op tijdstip t = 0 vertrekt uit Vlieland  boot A naar Harlingen  met een snelheid van 20 km/uur. Tegelijkertijd vertrekt vanuit Harlingen boot B naar Vlieland. Die gaat vanwege de wind en de getijden sneller, nl.  25 km/uur
a. Geef één formule voor de afstand y tussen beide boten als functie van de tijd t. Denk eraan dat de afstand altijd positief moet zijn.
   
y = │45t - 27,4 │
De beide kapiteins kunnen via de mobilofoon contact met elkaar hebben, maar dan moet hun afstand minder dan 8 km zijn.
b. Bereken hoe lang de bestuurders via de mobilofoon contact kunnen hebben.
       
211/3 minuut
         
5. Een luie wiskundige moet de wortel trekken uit een groot aantal getallen tussen 0 en 1.
Hij heeft echter alleen een gewone simpele rekenmachine waar geen wortelknop op zit.
Daarom benadert hij die wortels eenvoudig door te zeggen dat  √x » 0,7x + 0,2
Hij zegt dus bijvoorbeeld  √(0,1) = 0,7 • 0,1 + 0,2 = 0,27 terwijl dat eigenlijk gelijk is aan 0,316227766....
De afwijking (A) is hoe ver hij met zijn benadering naast de werkelijke waarde van √x zit. (in het voorbeeld 0,046...)
         
  a. Schets de grafiek van A(x)
         
  b. Wat is de grootste afwijking die hij kan krijgen?

0,157
   
6.
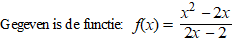  Los op:  | f(x) | ≥ 1/4x
       
〈←, 1〉 en 〈12/3] en [12/3,→〉
         
7. Als  | x | + y = 10  en   x + y = 2,  waaraan is x - y dan gelijk?
       

-10
8. Voor hoeveel natuurlijke getallen geldt:  |√n - 7| < 1 ?
       

27
       

© h.hofstede (h.hofstede@hogeland.nl)