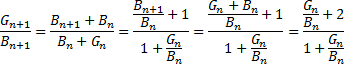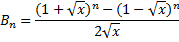© h.hofstede (h.hofstede@hogeland.nl)

Wortels benaderen.
       
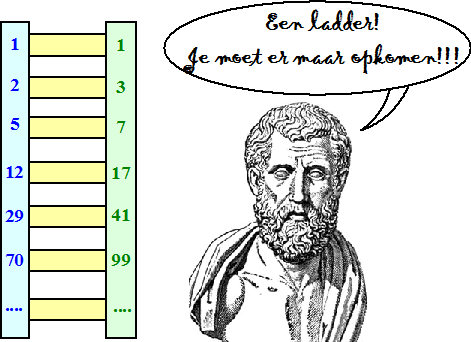
De oude Griek Theon van Smyrna had een coole manier om de wortel van 2 te benaderen. Dat deed hij door als volgt een "ladder" van getallen te maken, van boven naar beneden:
       

       
Een blauw getal is steeds gemaakt door de twee getallen (groen plus blauw) op de trede erboven bij elkaar op te tellen. Een groen getal is die nieuwe blauwe plus de vorige blauwe.
Als je nu twee getallen op dezelfde trede van de ladder op elkaar deelt  (groen gedeeld door blauw),  krijg je de serie:
1/1 = 1
3/2 = 1,5
7/5 = 1,4
17/12 ≈ 1,41666
41/29 ≈ 1,41379
99/70 ≈ 1,41429
Dat loopt langzaam naar √2 (1,414213562...) toe.
       
Waarom gaat die ladder naar √2?
       
Noem de blauwe op trap n gelijk aan Bn en de groene aan Gn, dan gelden volgende recursievergelijkingen;
Bn+1  = Bn + Gn
Gn+1 = Bn+1 + Bn  
op elkaar delen geeft als benadering:

Maar als er een limiet bestaat dan wordt die verhouding  Gn+1/Bn+1 = Gn/Bn constant, en kunnen we die gelijk stellen aan L (van limiet)
Dan staat hierboven   L = (L + 2)/(1 + L)
Dat geeft  L(1 + L) = L + 2  ⇒  L + L2 = L + 2  ⇒  L2 = 2  ⇒  L = √2
       
Kunnen we er ook andere wortels mee benaderen?
       
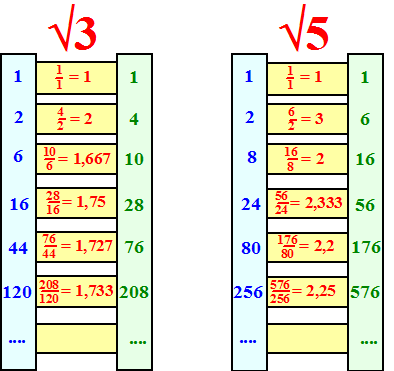
Tuurlijk;  kijk maar waar die 2 in L2 = 2 vandaan kwam:  volg de "weg terug"  en je ziet dat dat komt van de factor 1 in de recursievergelijking  Gn+1 = Bn+1 + 1 • Bn.  Die 2 was één meer dan de 1 uit deze vergelijking.
Dat betekent dat we voor √3 gewoon die 1 door een 2 vervangen , en voor √5 die 1 door een 4
Voor de benadering van √x  geeft dat  de volgende recursievergelijkingen:
       

Benaderen van √x:

Bn+1  = Bn +  Gn
Gn+1 = Bn+1 + (x - 1) • Bn

       
Dat geeft bijvoorbeeld de volgende ladders voor √3 en √5 

       
Kan het niet wat sneller?
       
De waarden die deze vergelijkingen als benadering opleveren lopen wel erg langzaam naar de exacte wortel toe.  Er is echter een mooie methode om dat proces wat te versnellen.
Waarom zou je bij het beklimmen (of in dit geval afdalen)  van een ladder niet wat treden over mogen slaan?

We bewijzen daarvoor eerst dat geldt:  Gn + √x • Bn =  (1 + √x)n

Dat bewijzen we met volledige inductie:
  Het geldt voor n = 1, want dat geeft  G1 + √x • B1 = 1 + √x  en met  G1 = B1 = 1  klopt dat.
Stel dat het klopt voor bepaalde N....  (de inductie-aanname)
(1 + √x)N + 1
= (1 + √x)N • (1 + √x)
= (GN + √x • BN) • (1 + √x)     (de inductie-aanname)
=  xBN + GN  + √x • GN + √x • BN  (haakjes wegwerken)
=  (xBN + GN) + √x(GN + BN)    (hergroeperen)
=  (xBN + GN) +  √x • BN+1      (recursievergelijking voor BN)
=  (x - 1)BN + BN + GN + √x • BN+1
=  (x - 1)BN + BN+1 + √x • BN+1    (resursievergelijking voor BN)
=  GN+1 + √x • BN+1 
Dus dan klopt het ook voor N + 1 
q.e.d.

(op dezelfde manier kun je trouwens ook de verwante relatie GN - √x • BN = (1 - √x)n  bewijzen)

Maar als die vergelijking voor elke n geldt, dan geldt hij dus ook voor 2n:
G2n + √x • B2n =  (1 + √x)2n
= ((1 +√x)n)2
= (Gn + √x • Bn)2
= Gn2 + 2Gn√xBn + xBn2
= (xBn2 + Gn2) + √x(2BnGn)  en dat moet gelijk zijn aan  G2n + √x • B2n

Dus dan is:

B2n = 2BnGn
G2n = xBn2 + Gn2
       
Kijk! Dat schiet tenminste op.
Als we bijvoorbeeld B10  en G10 hebben, dan kunnen we daaruit in één stap B20 en G20 berekenen.
En daaruit dan weer B40 en G40.
En dan B80 en G80.
We gaan met steeds grotere reuzenstappen de ladder af.
       
Kan het niet nóg wat sneller?
       
Er is zelfs een directe formule voor Bn en Gn af te leiden!! Maar dat is wel een beetje lastiger......

Bn + 1 = Bn + Gn    maar  Gn = Bn + (x - 1)Bn - 1
invullen van de tweede in de eerste geeft:   Bn + 1 = Bn + Bn + (x - 1)Bn - 1
Bn + 1  = 2Bn + (x - 1)Bn - 1
Bn + 2 = 2Bn + 1 + (x - 1)Bn

(Wat we nu moeten oplossen heet een lineaire tweede-orde-differentievergelijking. In deze les staat preciezer hoe dat moet, wat hier volgt is een een korte afleiding).

Laten we nou voor de grap eens proberen of misschien een machtsfunctie  Bn = a • pn   een oplossing is. 
Invullen dus maar:
apn + 2 = 2apn + 1 + (x - 1)apn    en dat kun je delen door  apn :
p2 = 2p + (x - 1)
p2 - 2p - (x - 1) = 0
ABC-formule:    p = (2 ±√(4 + 4(x - 1))/2  = (2 ± 2√x)/2 = 1 ± √x
We vinden dus de twee mogelijke oplossingen   Bn = a(1 + √x)n  en  Bn = b(1 - √x)n  

Stel dat we als meest algemene oplossing een combinatie van beiden nemen:  Bn = a(1 + √x)n  +  b(1 - √x)n  
We willen verder ook nog graag dat  B1 = 1 en B2 = 2  (kijk maar naar de ladders hierboven, dat is steeds zo))
Dan moet gelden:   a(1 + √x) + b(1 - √x) = 1   en   a(1 + √x)2 + b(1 - √x)2 = 2
De eerste geeft   a(1 + √x) = 1 - b(1 - √x)  = 1 - b + b√x  en dat kun je invullen in de tweede:
(1 - b + b√x)(1 + √x) + b(1 - √x)2 = 2
1 + √x - b - b√x + b√x + bx + b - 2b√x + bx = 2
√x + 2bx - 2b√x = 1
2b(x - √x) = 1 - √x
b = (1 - √x)/2√x(√x - 1)  = -1/2√x  
Dan is  a(1 + √x)  =  1 - b + b√x  = 1 + 1/2√x - 1/2 = 1/2(1 + 1/√x) = 1/2√x • (√x + 1)
Dat betekent dat  a = 1/2√x
Conclusie:

       
Dat schiet nóg meer op.
Daaruit zie je bijvoorbeeld direct dat (voor de berekening van √2) geldt:  B29 = 44560482149  en  B30 = 107578520350
Dus  G30 = 44560482149  +  107578520350 = 152139002499
dat geeft als dertigste benadering:  √2 = 152139002499 /107578520350 = 1,414213562.....
       
       

© h.hofstede (h.hofstede@hogeland.nl)