| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Teken de eerste vier stappen
in een webgrafiek voor de recursievergelijking u(n)
= 0,9u(n - 1) + 10 met u0
= 10. |
| |
|
|
|
| 2. |
a. |
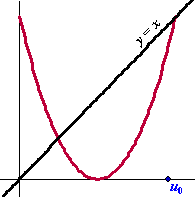
Teken de eerste vier stappen
van de tijdgrafiek die bij onderstaande webgrafiek hoort. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
b. |
Als je oneindig veel stappen zou tekenen, wat
zijn dan de mogelijke waarden voor u¥? |
| |
|
|
|
| 3. |
Gegeven is de rij getallen un
met recursievergelijking un = 6/u(n-1)
+ 1 |
| |
|
|
|
| |
a. |
Bereken in vier decimalen nauwkeurig u10 als
u0
= 2 |
| |
|
|
| |
b. |
Deze rij nadert naar een grenswaarde. Bepaal deze
grenswaarde eerst met je GR en daarna exact algebraïsch. |
| |
|
|
|
| |
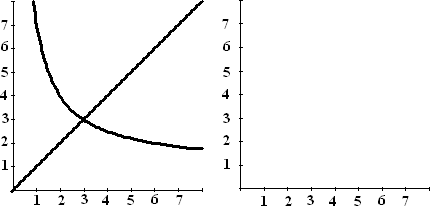
Hieronder staan in de linkerfiguur de grafieken
van y = x en y = 1 + 6/x getekend. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
c. |
Teken in deze figuren de eerste 4
stappen van een webgrafiek en van een tijdgrafiek als u0
= 1. Doe dat zonder berekeningen te maken. |
| |
|
| 4. |
Gegeven is
de rij getallen un met un
= un-12 – 6un-1
+ 10 |
| |
|
|
|
| |
a. |
Neem u0 = 2,8 en bereken
u20 in vier decimalen nauwkeurig.
|
| |
|
|
|
| |
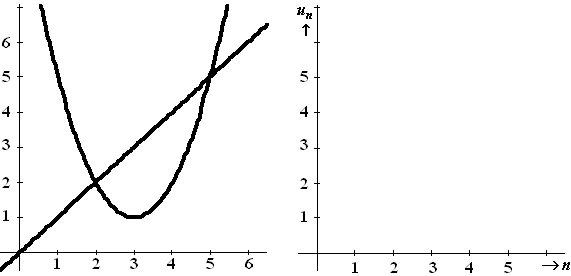
Hieronder zie je de grafieken van y = x en
y
= x2 – 6x + 10 |
| |
|
|
|
| |
b. |
Neem u0 = 3,5 en teken 4
stappen van de webgrafiek. Teken ook vier stappen van de tijdgrafiek in de rechterfiguur.
|
| |
|
|
|
| |
 |
| |
|
|
|
| 5. |
examenvraagstuk VWO wiskunde B,
2003
Gegeven is de rij: |
| |
|
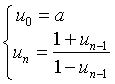 |
| |
In de volgende twee vragen
kiezen we de startwaarde a = 2
In de figuur hieronder staat de webgrafiek bij deze startwaarde. |
| |
|
|
|
| |
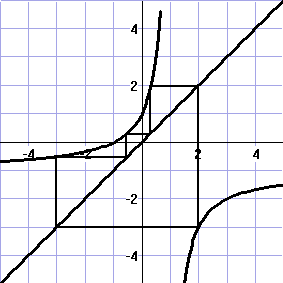 |
| |
|
|
|
| |
a. |
Bereken u1,
u2, u3 en u4. |
|
| |
|
|
|
| |
b. |
Bereken u999999.
Licht je antwoord toe. |
|
| |
|
|
|
| |
We kunnen ook andere
startwaarden a nemen dan 2. Als we a = 0 nemen, heeft de
rij maar twee termen: u0 en u1; dan
is de term u2 namelijk niet gedefinieerd.
Behalve a = 0 is er nog een startwaarde waarbij één van de
termen in de rij un gelijk is aan 0. De daaropvolgende
term in de rij is dan niet gedefinieerd. |
| |
|
|
|
| |
c. |
Welke startwaarde is dat? Licht je
antwoord toe. |
|
| |
|
|
|
| |
In de rest van deze opgave
werken we met startwaarden waarbij u1, u2 en u3
wél gedefinieerd zijn. Bij zo'n startwaarde a kun je
achtereenvolgens u1 en u2
bepalen. |
| |
|
|
|
| |
d. |
Toon langs algebraïsche weg
aan dat de uitdrukking die je voor u2 krijgt kan
worden
vereenvoudigd tot -1/a |
| |
|
|
|
| |
Nu je u2
hebt gevonden kun je u4 ook bepalen. |
| |
|
|
|
| |
e. |
Toon aan dat u4 = a |
|
| |
|
|
|
| 6. |
Examenvraagstuk VWO, Wiskunde B,
2003. Gegeven zijn de
functies f`(x) = 1/4x2
en g(x) = -4/x²
Bij een startwaarde u0
> 0 is de rij van positieve getallen un gedefinieerd
door un= f(un-1).
De rij van negatieve getallen vn is gedefinieerd door vn
= g(un).
In de figuur hieronder zijn de plaats van u0 op de x-as,
de grafieken van f en g en de lijn y = x
getekend. |
| |
|
|
|
| |
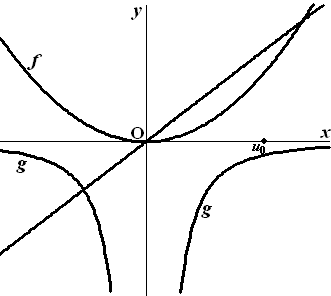 |
| |
|
|
|
| |
a. |
Teken in bovenstaande figuur de plaats van v2
op de x-as. |
| |
|
|
|
| |
b. |
Bij een bepaalde startwaarde van
u0 krijgt v1 de waarde -1. Bereken deze startwaarde u0 |
| |
|
|
|
| |
|
|
|
| 7. |
Examenvraagstuk VWO Wiskunde B,
2007. |
| |
|
|
|
| |
| De functie f is gegeven door: |
|
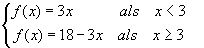
|
|
| |
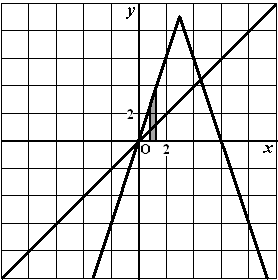
In de figuur hiernaast is de
grafiek van f getekend, evenals
de lijn y = x
Bij elke startwaarde s is
er een rij u0, u1, u2,
... vastgelegd door:
Neem s = 5. Bij deze startwaarde vertonen de termen van de
rij vanaf n = 3 een bepaalde regelmaat. |
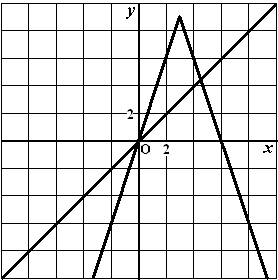 |
| |
|
|
| |
a. |
Geef voor n ≥
3 een directe formule waarin je un
uitdrukt in n. Licht je
antwoord toe. |
| |
|
|
|
| |
Er zijn startwaarden waarvoor de rij
bestaat uit twee verschillende getallen die elkaar
afwisselen. Dus u2 = u0. |
| |
|
|
|
| |
b. |
Eén van die startwaarden is groter dan
5. Bereken deze startwaarde exact. |
| |
|
|
|
| |
We bekijken het gedrag van de rij
voor startwaarden tussen
5/6 en
7/6.
Veronderstel dat je voor alle startwaarden
tussen 5/6 en
7/6
de eerste stap tekent van de
webgrafiek. In de figuur hiernaast is de strook die
dan ontstaat met grijs aangegeven.
Wanneer je voor
alle startwaarden tussen 5/6 en
7/6
het vervolg van de webgrafiek
tekent, ontstaat het vervolg van de strook. |
 |
| |
|
|
| |
c. |
Onderzoek met behulp van de
figuur of de rijen met startwaarden tussen
5/6
en 7/6 convergeren. |
| |
|
|
|
|
|
|
|
|
|
|
|