© h.hofstede (h.hofstede@hogeland.nl)

       
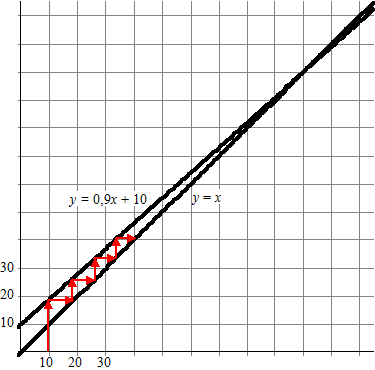
1. Hieronder zijn de lijnen y = x  en y = 0,9x + 10 getekend met de webgrafiek:
       
 

       
2. a.

       
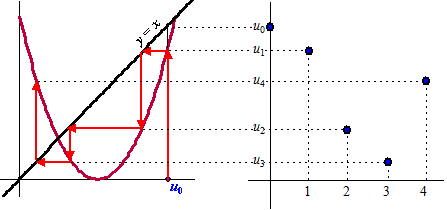
  b. De snijpunten van de parabool met de lijn y = x zijn mogelijkheden, maar of de rij ook werkelijk naar die waarden toegaat is niet te zeggen.
       
3. a. mode seq
nMin = 0
u(n) = 6/u(n - 1) + 1
u(nMin) = 2
TABLE geeft dan u10 = 2,9784
       
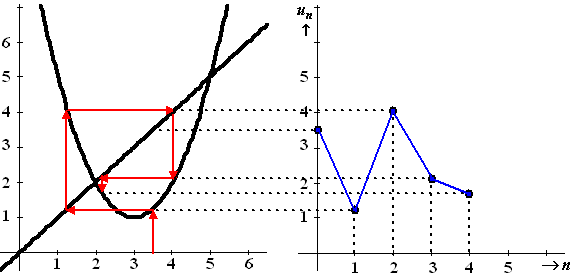
  b. Kijk in  TABLE bij erg grote waarden van n.
Dat loopt naar  u = 3 toe

evenwicht:   u = 6/u + 1
u2 = 6 + u
u2 - u - 6 = 0
(u - 3)(u + 2) = 0
u = 3 ∨ u = -2
Met deze beginwaarde geldt kennelijk u = 3
       
  c.
       
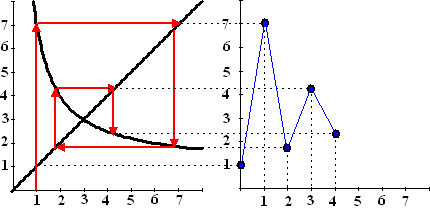4. a. mnode seq
nMin = 0
u(n) =   u(n -1)^2 – 6u(n-1)  + 10
u(nMin) = 2,8
TABLE en dan bij n = 20  geeft u20 = 1,0816
       
  b.

       
5. a. u0 = 2 
⇒  u1 = (1 + 2)/(1 - 2)= -3 
⇒  u2 = (1 + - 3)/(1 - -3) = -0,5
⇒  u3 = (1 + -0,5)/(1 - -0,5) = 1/3 
⇒ u4 = (1 + 1/3)/(1 - 1/3) = 2
       
  b. Omdat u4 = u2 gaat het rijtje  2 , -3 , -0,5 , 1/3 ,....... zich alsmaar herhalen.
Elk nummer dat een veelvoud van 4 is, geeft  daarom weer u = 2.
Dus ook u999996 = 2 en dan is u999999 gelijk aan  u3 = 1/3
       
  c. u1 = 0  ⇒  (1 + a)/(1 - a) = 0  ⇒  1 + a = 0  ⇒  a = -1
       
  d.
       
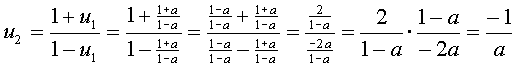  e.
       
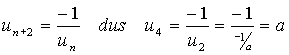6. a.

       
  b. u0 = x ⇒  u1 = 1/4x2 Þ  u2 = 1/4(1/4x2)2 = 1/64x4
   
       
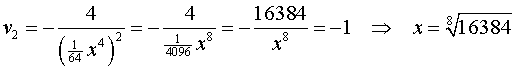7. a. 5 → 3 → 9 →  -9 → -27  →  -81   ...
Zodra un is negatief wordt het met 3 vermenigvuldigd. Daardoor blijft het negatief en wordt de volgende keer wéér met 3 vermenigvuldigd. Kortom: we blijven de bovenste van beide formules voor f gebruiken.
De formule zal zijn van de vorm  un = B • 3n
Omdat u3 = -9  moet gelden:  -9 = B • 33  ofwel  B = -1/3  en de formule is  un = -1/3 • 3n  (of un = 3n-1)
       
  b. Stel, u0 = x
Dan is  u1 = 18 - 3x  (immers  x > 5)
Er zijn twee mogelijkheden:

Als u1 < 3 dan geldt  u2 = 3u1 = 3(18 - 3x) en dat moet gelijk zijn aan u0 dus aan  x
3(18 - 3x) = x  ⇒  54 - 9x = x  ⇒  10x = 54  ⇒  x = 5,4
u0 = 5,4  ⇒  u1 = 1,8  ⇒   u2 = 5,4  KLOPT!

Als u1 > 3 dan geldt  u2 = 18 - 3u1 = 18 - 3(18 - 3x) = 18 - 54 + 9x = 9x - 36
Dat moet gelijk zijn aan u0 dus aan x:  9x - 36 = x  ⇒  8x = 36  ⇒  x = 4,5
Maar dat klopt niet want dat is niet groter dan 5.

Conclusie:  u0 = 5,4
       
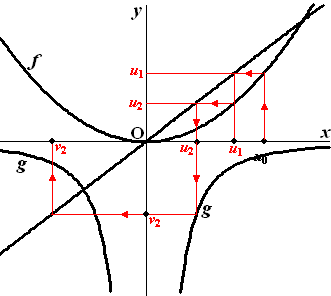
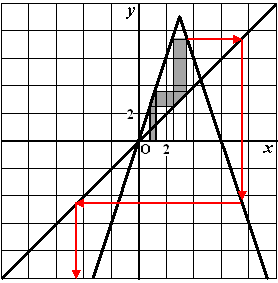
  c. Hiernaast zie je dat het grijze gebied na twee keer reduceert tot de rode lijn!
En die divergeert duidelijk, dus elke rij met startwaarde uit het grijze gebied divergeert.
(ze gaan allemaal de rode lijn volgen)
       

© h.hofstede (h.hofstede@hogeland.nl)