| |
 |
|
De vergelijking van een vlak. |
ę
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
Om langzaamaan een idee te
krijgen van hoe de vergelijking van een vlak er uit ziet, beginnen we
eerst maar eens met een paar eenvoudige vergelijkingen. Nou ja ...
eenvoudig.... je kunt beter zeggen kinderlijk eenvoudig.
EÚn van de allersimpelste vergelijkingen die mij zo te binnen schiet is
de vergelijking x = 3 |
De vraag is dus: "Waar
liggen de punten waarvoor geldt x = 3, en hoe ziet de verzameling
van al die punten er uit?"
Je kunt om dat te ontdekken er natuurlijk gewoon een aantal gaan
tekenen.
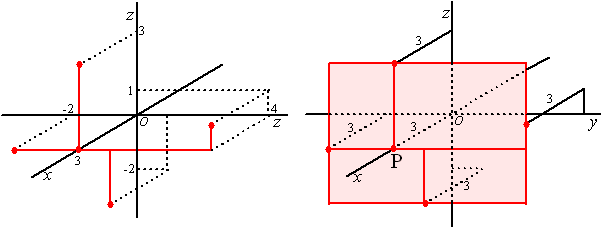
Bijvoorbeeld (3, 4, 1) en (3, 0, 0) en (3, -2, 0) en (3, 0, 3) en
(3, 2, -2) en .....
Die vijf punten zijn hieronder links getekend, met wat hulplijntjes om
de plaats duidelijker aan te geven. |
| |
|
|
|
|
 |
| |
|
|
|
Ze liggen allemaal in
een plat vlak dat door punt P(3, 0, 0) gaat en dat evenwijdig aan het
Oyz vlak is (dat is het vlak waar de y-as en de z-as
in liggen). Dat vlak is hier rechtsboven getekend. Het is eigenlijk het
Oyz vlak, maar dan 3 "naar voren geschoven".
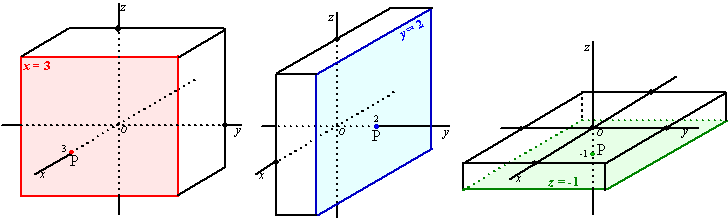
Op precies dezelfde manier kun je bijvoorbeeld de vlakken y = 2
en z = -1 tekenen. Die zie je in de volgende figuur. |
| |
|
|
|
|
 |
| |
|
|
|
| EÚn rode draad (die
later ook nog handig zal blijken te zijn) kun je alvast uit deze figuren
leren: |
| |
|
|
|
|
Als x, y of z
niet in de vergelijking staat,
is het vlak evenwijdig aan die as. |
|
| |
|
|
|
Dat kun je natuurlijk
ook zˇ beredeneren:
Stel dat de y niet in de vergelijking voorkomt. Als je dan een
punt P van het vlak hebt dan kloppen de co÷rdinaten van P met de
vergelijking. Maar als je nu in de y-richting beweegt, dan
verandert alleen de y-co÷rdinaat van P, maar die doet er nou
juist voor de vergelijking niet toe. Ofwel: als je vanaf P in de
y-richting gaat bewegen, dan voldoen de co÷rdinaten van alle
nieuwe punten die je krijgt ook aan de vergelijking, dus liggen die
nieuwe punten ook allemaal in het vlak.
Dan is dat vlak evenwijdig aan de y-richting. |
| |
|
|
|
|
Moeilijkere Vergelijkingen. |
| |
|
|
|
Neem de vergelijking
2x + 3y + 2z = 12.
Die gaan we onderzoeken.
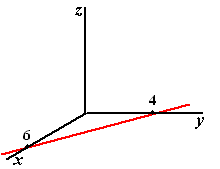
Laten we eerst het 2D-geval bekijken, als z = 0
Dan staat er 2x + 3y = 12 en dat
is een rechte lijn in het Oxy-vlak.
(gaat bijvoorbeeld door (6,0) en (0,4))
Je ziet hem hiernaast.
|
 |
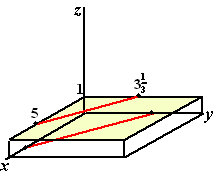
Neem nu het geval
z = 1.
Dan staat er 2x + 3y = 10, en dat is ook een rechte
lijn, nu alleen in het vlak z = 1. Daarin gaat hij door
bijvoorbeeld (5, 0) en (0, 31/3)
Je ziet hem hiernaast erbij getekend.
Hij is evenwijdig aan die andere rode lijn, want alleen het getal 10 is
in 12 veranderd, en dat verandert de helling niet.
Nou, en zo kun je alsmaar doorgaan.
|
 |
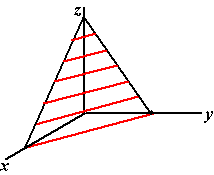
Hiernaast zie je de
doorsnedes met de vlakken z = 0 tot en met z = 6
Als die rode lijntjes vormen samen ons gezochte vlak Ze lopen natuurlijk
aan de zijkanten nog door; alleen het stukje met alle co÷rdinaten
positief is getekend)
Dat lijkt inderdaad een plat vlak te zijn.
De echte achterdochtigen onder ons kunnen daar nog aan twijfelen. Die
zullen zeggen "OK, al die rode lijntjes lopen evenwijdig, maar dat
wil nog niet zeggen dat ze in een plat vlak liggen, die zwarte randen
zijn misschien wel krom..." |
 |
| Maar als je je
bedenkt dat we dit hele verhaal ook kunnen houden voor doorsnedes met
vlakken y = 0, y = 1, ... en x =
0, x = 1, .... en dat we dan elke keer evenwijdige lijnen vinden,
dan zul je niet anders dan kunnen toegeven dat dit toch echt een plat
vlak voorstelt. |
| |
|
|
|
|
ax + by + cz =
d is de vergelijking van een plat vlak. |
|
| |
|
|
|
| Om zo'n vlak te
tekenen is het vaak handig om de snijpunten met de co÷rdinaatassen te
tekenen. En bedenk je verder nog, dat als er een x, y of
z mist in de vergelijking, dat dan het vlak evenwijdig is aan die
co÷rdinaat-as. |
| |
|
|
|
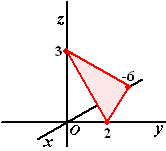
| Voorbeeld
1. |
Teken het vlak met
vergelijking -x + 3y + 2z = 6.
Bereken de snijpunten met de co÷rdinaatassen:
x = 0 en y = 0 geeft z = 3 en het punt (0,0,3)
x = 0 en z = 0 geeft y = 2 en het
punt (0, 2, 0)
y = 0 en z = 0 geeft x = 6 en het punt (-6, 0,
0)
Dat geeft het vlak hiernaast. |
 |
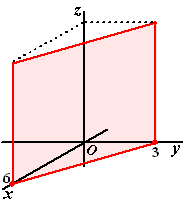
| Voorbeeld
2. |
|
Teken het vlak met
vergelijking 2x + 4y = 12
Bereken de snijpunten met de co÷rdinaatassen:
x = 0 en z = 0 geeft y = 3 en het punt
(0, 3, 0)
y = 0 en z = 0 geeft x = 6 en het punt
(6, 0, 0
x = 0 en y = 0 geeft....NIETS.
z staat niet in de vergelijking dus het vlak is evenwijdig aan de
z-as.
Dat geeft het vlak hiernaast. |
 |
| |
|
|
|
TRAP ER NIET IN!
De vergelijking y = ax + b is dus in 3D geen
vergelijking meer van een lijn!.
Het is een plat vlak evenwijdig aan de z = as.
Een lijn is eenvoudigweg in 3D niet door ÚÚn vergelijking weer te geven.
Als je een lijn toch wilt weergeven dan kun je dat doen door TWEE
vergelijkingen (de lijn is dan eigenlijk de snijlijn van de twee vlakken
van die vergelijkingen).
Het kan op een veel mooiere manier met vectoren, maar ja, dat is weer
een heel ander en heel uitgebreid onderwerp (dat kun je vinden in de
W-lessen). |
| |
|
|
|
| |
|
|
|
|
| 1. |
Teken de volgende vlakken: |
| |
|
|
|
|
| |
a. |
4x - 2y +
z = 16 |
| |
|
|
|
|
| |
b. |
2x + y - 5z =
10 |
|
|
| |
|
|
|
|
| |
c. |
2y + 4z = 12 |
|
|
| |
|
|
|
|
| |
d. |
3x = 18 - 2z |
|
|
| |
|
|
|
|
| 2. |
De vergelijking x2
+ y2 = 4 is in 2D een vergelijking van een
cirkel met middelpunt de oorsprong en straal 2. |
| |
|
|
|
|
| |
a. |
Hoe ziet de grafiek van
deze vergelijking in 3D eruit? |
| |
|
|
|
|
| |
b. |
Hoe ziet de grafiek (3D)
van y2 + z2 = 4 eruit? |
| |
|
|
|
|
| 3. |
examenvraagstuk VWO
Wiskunde B, 1985. |
| |
|
|
|
|
| |
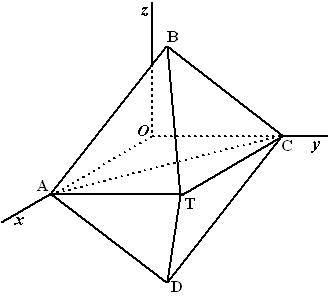
Ten opzichte van een rechthoekig
assenstelsel Oxy zijn gegeven de punten A(12,0,0), C(0,12,0)
en T(12,12,0).
Deze punten zijn hoekpunten van een regelmatige vierzijdige piramide
T.ABCD met top T.
Het punt E is het midden van ribbe BC. |
 |
| |
|
|
|
| |
a. |
Teken in de ruimtefiguur hiernaast de
doorsnede van de piramide en het vlak met vergelijking y = 8.
Geef een korte toelichting bij de tekening.
Bereken de oppervlakte van deze doorsnede. |
| |
|
|
|
| |
b. |
De lijn AC snijdt het vlak met vergelijking
y = 8 in het punt S. Bereken de co÷rdinaten van S. |
| |
|
|
|
|
| 4. |
examenvraagstuk VWO
Wiskunde B, 1987. Ten opzichte van
een rechthoekig assenstelsel Oxyz is de piramide T.OABC gegeven
door O(0,0,0), A(6,0,0), B(6,6,0), C(0,6,0) en T(0,0,8) |
| |
|
|
|
|
| |
a. |
Punt P is het
midden van lijnstuk BT.
De lijn PC snijdt het vlak OAT in het punt S.
Teken in een ruimtefiguur de piramide T.OABC en construeer het punt S.
Bereken de co÷rdinaten van S. |
| |
|
|
|
|
| |
b. |
De loodrechte
projectie op het Oxy-vlak van de doorsnede van de piramide met
het vlak met vergelijking
x + 2/3y
+ 2z = 8 is een vijfhoek V.
Bereken de oppervlakte van V. |
| |
|
|
|
|
|
|
Van vlak naar vergelijking. |
| |
|
|
|
|
Het kan natuurlijk ook dat er een vlak is getekend
waarvan je graag de vergelijking zou willen hebben.
In principe kun je die altijd vinden als je maar 3 punten (die niet op
ÚÚn lijn liggen) van dat vlak kunt vinden.
Waarom?
Nou, de algemene vergelijking van een vlak was ax + by +
cz = d maar als je alles door d deelt, dan
krijg je een algemene vergelijking px + qy + rz = 1
(p, q en r zijn nieuwe constanten).
Vul de drie gevonden punten in, en je krijgt een stelsel van drie
vergelijkingen met drie onbekenden. Dat is op te lossen....
En als het vlak evenwijdig is aan een co÷rdinaat-as, dan heb je zelfs
minder punten nodig omdat de x, y of z waaraan het
vlak evenwijdig is, ontbreekt in de vergelijking.
de assenvergelijking. |
| |
|
|
|
Als je de snijpunten
van een vlak met de co÷rdinaatassen hebt, dan kun je heel snel daar een
vergelijking van opstellen.
Die ziet er zˇ uit: |
|
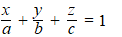 |
| |
|
|
|
En daarin zijn de
snijpunten met de co÷rdinaatassen achtereenvolgens x = a
en y = b en z = c
Dat dat inderdaad zo is kun je heel snel controleren. Vul voor
bijvoorbeeld het snijpunt met de x-as maar y = 0 en z =
0 in de vergelijking in. Dat geeft x/a
= 1 dus inderdaad x = a.
Voorbeeld 3.
Geef een vergelijking van het vlak door (3, 0, 0) en (0, 5, 0)
en (0, 0 ,-2)
De assenvergelijking geeft in ÚÚn keer x/3
+ y/5 + z/-2 =
1
Vermenigvuldig alles met 30 en je krijgt de wat mooiere uitdrukking:
10x + 6y - 15z = 30 |
| |
|
|
|
| |
|
|
|
|
| 5. |
Geef een vergelijking van de volgende vlakken: |
| |
|
|
|
|
| |
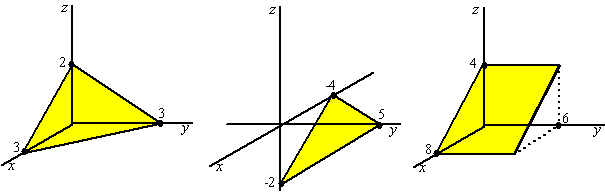 |
| |
|
|
|
|
| |
|
| |
|
|
|
|
| 6. |
Geef een vergelijking van de
volgende vlakken |
| |
|
|
|
|
| |
a. |
Door (2, 2, 2)
en (1, 2, 4) en (-1, 4, 2) |
| |
|
|
|
|
| |
b. |
Door (2, 4,
7) en (1, -10, 3) en (-4, 8, 5) |
| |
|
|
|
|
| |
|
|
|
|
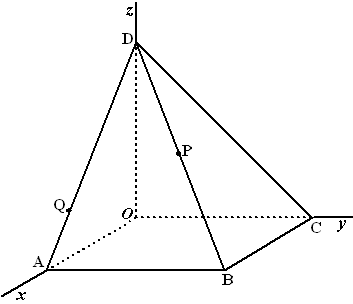
| 7. |
examenvraagstuk VWO
Wiskunde B, 1985. Ten opzichte van
een rechthoekig assenstelsel Oxyz zjin gegeven de punten
A(8,0,0), B(8,8,0), C(0,8,0) en D(0,0,8).
Deze punten zijn de hoekpunten van een vierzijdige piramide D.ABCO.
Punt P is het midden van ribbe BD en punt Q ligt op ribbe AD zo dat AQ :
QD = 1 : 3.
V is het vlak door P, evenwijdig aan de lijn BQ en evenwijdig aan de
lijn DO.
Teken in de figuur hieronder de
doorsnede van V met de piramide.
Geef daarbij een korte toelichting.
Stel een vergelijking op van V. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
|
|
ę
h.hofstede (h.hofstede@hogeland.nl) |
|
 |