Taylor-reeksen

© h.hofstede (h.hofstede@hogeland.nl)
       
Deze les gaan we op zoek naar reeksontwikkelingen die niet zo erg afhangen van 1/(1 - x), zoals in de vorige les.

Deze hele les hangt aan elkaar van twee aannames, en dat zijn de volgenden:
We bekijken alleen functies waarvoor geldt:
       
1.  Er bestaat een reeksontwikkeling voor f.
2.  Je kunt  f  zo vaak als je maar wilt differentiëren.
       
Stel dat de reeksontwikkeling bij x = a er zó uitziet:

Nu kun je die c's één voor één vinden. Op de volgende manier:
   
1. Vul x = a in, dat geeft:  f(a) = c0   (en de rest wordt allemaal nul)
       
2. Voor de afgeleide geldt  f '(x) = c1 + 2c2(x - a) + 3c3(x - a)2 + ...
Vul nu x = a in, dat geeft:  f '(a) = c1  (en de rest wordt allemaal nul)
   
3. Voor de tweede afgeleide geldt:  f ''(x) = 2c2 + 2 • 3c3(x - a) + 3 • 4 c4(x - a)2
Vul nu x = a in, dat geeft:  f ''(a) = 2c2  (en de rest wordt allemaal nul), 
dus c2 = 1/2 • f ''(a)
       
4. Voor de derde afgeleide geldt: 
f '''(x) = 2 • 3c3 + 2 • 3 • 4 c4(x- a) + 3 • 4 • 5 • c5(x - a)2 + ...
Vul nu x = a in, dat geeft:  f '''(a) = 2 • 3c3  (en de rest wordt allemaal nul), 
dus c3 = 1/(2•3) • f '''(a)
       
enzovoorts. Ik hoop dat het patroon duidelijk is.
Het eindresultaat ziet er zó uit  (met f (n) wordt bedoeld: de nde afgeleide):
       

       
Dit mooie regelmatige resultaat heet een Taylorreeks (naar de Engelse wiskundige Brook Taylor die er zo rond 1715 mee op de proppen kwam).

In formule:

 
Als de reeks rond x = 0 plaatsvindt (dus met a = 0) dan wordt het ook wel een MacLaurin-reeks genoemd.
       
Een paar beroemde voorbeelden.
       
Beroemd voorbeeld 1:  De reeksontwikkeling van ex  rond x = 0
De afgeleide is weer ex dus dat geeft steeds dezelfde f(n)(0) = e0 = 1.
       
Beroemd voorbeeld 2. De reeksontwikkeling van sinx rond x = 0.
De afgeleide is cosx, en daar weer de afgeleide van is -sinx, en dan is de volgende afgeleide -cosx, enz.
Dat geeft dit patroon:  sinx → cosx  → -sinx →  -cosx → sinx →.....
Maar steeds is sin0 = 0, dus alleen de termen met de oneven afgeleiden blijven over, en die zijn allemaal 1 of -1.
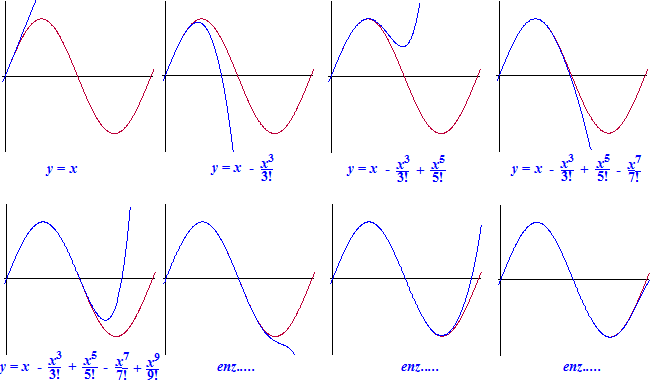
Hier zie je een stripverhaal van hoe dat er uitziet:
 

 
De blauwe grafieken gaan meer en meer op de rode grafiek van sinx lijken.

De reeksontwikkeling voor sinx rond  x = 1/4π  zier er in een stripverhaal zó uit:
 

 
Nu begint die blauwe grafiek zich vanaf x = 1/4π om de rode "heen te vouwen".
De reeks voor cosx rond x = 0 gaat op dezelfde manier:
       
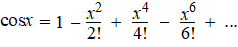Als je eenmaal zo'n reeks weet, kun je die soms gebruiken om weer anderen van af te leiden door een geschikte substitutie. Wil je bijvoorbeeld de reeksontwikkeling van e2x maken, dan kan dat snel door in de reeks van ex alle x-en door 2x te vervangen. Dan krijg je heel snel:
       
       
En voor een reeksontwikkeling van x3e2x  vermenigvuldig je nu gewoon alle met x3
       
       
De Taylorreeks van een polynoom.

Dat lijkt een nogal onnuttige bezigheid:  waarom zou je van zoiets eenvoudigs als een polynoom nou in hemelsnaam een Taylorreeks willen maken?  Ach, heel erg nuttig is dat ook niet, maar het levert eens een andere manier om zo'n polynoom weer te geven.
Neem bijvoorbeeld het polynoom  f(x) = 2x3 - 4x + 7, en laten we er een Taylorreeks rond het punt x = 2 van gaan maken.
f(2) = 15
f '(x) = 6x2 - 4  dus  f ' (2) = 20
f ''(x) = 12x  dus  f '' (2) = 24
f '''(x) = 12  dus  f ''' (2) = 12
de rest van de afgeleiden zijn allemaal nul.
Dat geeft als Taylorreeks: 
f(x) = 15 + 20/1 • (x - 2) + 24/2 • (x - 2)2 + 12/6 • (x - 2)3
=  15  + 20(x - 2) + 12(x - 2)2 + 2(x - 2)3  
Dat is een andere manier om het polynoom te noteren. Als je alle haakjes weg zou werken, dan kom je natuurlijk weer op het oorspronkelijke polynoom terecht......
       
De convergentiestraal
       
Een erg beroemde en veel gebruikte Taylorreeksontwikkeling is die van y = 1/(1 - x) rond x = 0
Dat geeft
f (0) = f '(0) = f ''(0) = f '''(0) = 1   (ga dat allemaal zelf maar na)

De reeksontwikkeling wordt dan   1/(1 - x) =   1 + x + x2 + x3 + .....
Maar kijk wat er gebeurt als we net als hierboven ook voor deze reeks een "stripverhaal"  tekenen: 
       

       
De blauwe grafiek gaat alleen voor x tussen -1 en 1 langs de rode lopen.  Daar aan de linkerkant blijft hij heen en weer schieten tussen plus-heel-groot en min-heel-groot. Daar aan de rechterkant wordt de grafiek heel groot (buiten beeld hierboven).
Dat komt natuurlijk omdat die reeks  1 + x + x2 + x3 + .....  alleen voor x tussen -1 en 1 convergeert.
Zo'n Taylorreeks geldt alleen op het gebied waar de reeks convergeert.  Dus bij deze reeks mag je vanaf  x = 0 niet meer dan 1 naar rechts en 1 naar links gaan.  Die afstand 1 heet de convergentiestraal van de reeksontwikkeling.

De convergentiestraal R van een reeks vind je het makkelijst door het criterium van Cauchy of dat van d'Alembert toe te passen (dat zagen we ook al bij machtreeksen in het algemeen):
 
       
 
       
       
         
  OPGAVEN
         
1.
         
2. a. Stel een Taylorreeks op voor f(x) = lnx  rond x = 1
         
  b. Stel een Taylorreeks op voor f(x) = e-x  rond x = 3
         
3. Geef de eerste vier termen van de reeksontwikkeling van f(x) = ex  • cosx  rond x = 0
         
4. In deze opgave gaan we een Taylorreeks voor f(x) = ln(1 + x)  rondom x = 0 bekijken.
         
  a. Maak die reeksontwikkeling.
         
  Maar  ln(1 + x) is ook de primitieve van 1/(1 + x)......
         
  b. Maak een staartdeling voor 1/(1 + x)  en neem daarna de primitieve daarvan.
Laat zien dat dat dezelfde reeksontwikkeling als in vraag a) oplevert.
         
5. Laat zien dat het convergentiegebied van de MacLaurinreeks voor f(x) = sinx  gelijk is aan R.
         
         
 
         
Leuke Toepassing:  Leid zelf een Gonio-formule af!

Laten we een reeksontwikkeling gaan maken voor sin(a + x)  rond x = 0. Bedenk daarbij dat de 1e, 2e, 3e...afgeleides achtereenvolgens  cos(a +x), -sin(a + x), -cos(a + x), enz. worden.
Laten we daarin de termen in twee groepen scheiden, afhankelijk of ze een sinus of een cosinus bevatten:
Maar daar tussen de haakjes staan nu precies de reeksontwikkelingen voor cosx en sinx
Dus geldt:   sin(a + x) = sina • cosx + cosa • sinx

Leuk he? Zelf een gonioformule afgeleid!!
       

© h.hofstede (h.hofstede@hogeland.nl)