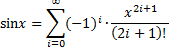|
|||||
| 1. | Bekijk de afgeleides van 1/x2 = x-2 rondom, x = -1 | ||||
| f (0)
= 1/x2
dus f (0)(-1) = 1 f (1) = -2x-3 = -2!/x3 dus f (1) (-1) = 2! f (2) = 6x-4 = 3!/x4 dus f (2)(-1) = 3! f (3) = -24x-5 = -4!/x5 dus f (3)(-1) = 4! enz. conclusie: f (n)(-1) = (n + 1)! Dat geeft in de Taylorreeks: f(x) = 2!/1! (x + 1)1 + 3!/2! (x + 1)2 + 4!/3! (x + 1)3 + .... f(x) = 2 (x + 1)1 + 3 (x + 1)2 + 4 (x + 1)3 + .... en dat is inderdaad de gegeven reeks. |
|||||
| 2. | a. | f (0)(x)
= lnx dus f (0)(1) =
ln1 = 0 f (1)(x) = 1/x dus f (1)(1) = 1 f (2)(x) = -1/x2 dus f (2)(1) = -1! f (3)(x) = 2/x3 dus f (3)(1) = 2 = 2! f (5)(x) = -6/x4 dus f (5)(1) = -6 = -3! enz. f (n)(1) = (-1)n+1 (n - 2)! |
|||
| Dan wordt de Taylorreeks: | |||||
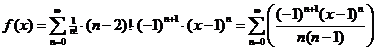 |
|||||
| Daarbij is gebruikt dat n! = n (n - 1) (n - 2)! | |||||
| b. | f (0)(x)
= e-x dus f (0)(3)
= e-3 f (1)(x) = -e-x dus f (1)(3) = -e-3 f (2)(x) = e-x dus f (2)(3) = e-3 enz. f (n)(3) = (-1)n e-3 Dan wordt de Taylorreeks: |
||||
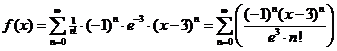 |
|||||
| 3. | f (0)(x)
= excosx dus f(0)(0)
= e0cos0 = 1 f (1)(x) = excosx - exsinx dus f (1)(0) = 1 f (2)(x) = excosx - exsinx - exsinx - excosx = -2exsinx dus f (2)(0) = 0 f (3)(x) = -2exsinx - 2excosx dus f (3)(0) = -2 f (4)(x) = -2exsinx - 2excosx - 2excosx + 2exsinx = -4excosx dus f (4)(0) = -4 |
||||
|
|
|||||
| 4. | a. | f (0)
(x) = ln(1 + x) dus f (0)(0)
= 0 f (1) (x) = (1 + x)-1 dus f (1) (0) = 1 f (2)(x) = -(1 + x)-2 dus f (2) (0) = -1 f (3) (x) = 2(1 + x)-3 dus f (3) (0) = 2 f (4) (x) = -2 3 (1 + x)-4 dus f (4)(0) = -2 3 f (5) (x) = 2 3 4 (1 + x)-5 dus f (5) (0) = 2 3 4 enz. Die afgeleiden vallen steeds, op één factor na, weg tegen de faculteiten: |
|||
| f(x) = x - 1/2x2 + 1/3x3 - 1/4x4 + 1/5x5 - 1/6x6 + .... | |||||
| b. |
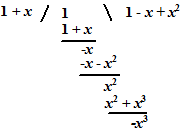 |
||||
| dus 1/(1
+ x) = 1 - x + x2 - x3
+ x4 - ... primitiveren: ln(1 + x) = x - 1/2x2 + 1/3x3 - 1/4x4 + 1/5x5 - 1/6x6 + .... |
|||||
| 5. | De MacLaurinreeks ziet er zó uit: | ||||
|
|
|||||
|
|
|||||
| En die laatste limiet is nul (dus < 1) voor alle x ∈ R | |||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||