som meetkundige rij

© h.hofstede (h.hofstede@hogeland.nl)

De som van een meetkundige rij.

Bij een rekenkundige rij was het vrij eenvoudig een formule te maken voor de som. Bij een meetkundige rij is dat helaas een stukje lastiger. Maar niet onmogelijk natuurlijk.
Oké, handen uit de mouwen dan maar.....

Een meetkundige rij ziet er in het algemeen uit als: b, ab, aab, aaab, aaaab, ...
Die b is het begingetal (afhankelijk van het verhaaltje u₀ of u₁), en die a is het "vermenigvuldiggetal" en heet ook wel de reden van de rij.
De rij kun je natuurlijk wat netter (en korter) schrijven als: b, ab, a²b, a³b, a⁴b, ...
Laten we de som van de eerste n termen van deze rij S_n noemen, dan geldt dus:

S_n = b + ab + a²b + a³b + a⁴b +... + aⁿb

Die S_n is niet zomaar uit te rekenen, maar er gebeurt iets leuks als we deze hele som met a vermenigvuldigen.
a • S_n = a • (b + ab + a²b + a³b + a⁴b +... + aⁿb) = ab + a²b + a³b + a⁴b + a⁵b + ... + aⁿ⁺¹b

"Nou nou, wat is hier leuk aan? Het wordt er alleen maar moeilijker van" hoor ik je al denken.
Maar kijk wat er gebeurt als we die S_n en a • S_n onder elkaar schrijven:

aS_n

= ab + a²b + a³b + a⁴b + ... + aⁿb + aⁿ⁺¹b

S_n

= b + ab + a²b + a³b + a⁴b + ... + aⁿb

Daar staat bijna hetzelfde!
Als je de onderste rij nu van de bovenste rij aftrekt, valt bijna alles weg, alleen die laatste term van de bovenste rij en die eerste term van de onderste rij blijven over:

aS_n - S_n = aⁿ⁺¹ b - b ⇒ S_n • (a - 1) = aⁿ⁺¹b - b

En daar is onze formule voor de som van een meetkundige rij al! b was het eerste getal van de rij, en b • aⁿ⁺¹ is het volgende getal van de rij (de eerste term die niet bij de som wordt genomen). Verder was a de reden van de rij.
Daarmee wordt onze formule in woorden:

De reden (J) dat je deze formule beter met woorden dan met variabelen kunt onthouden, is dat het op deze manier niet uitmaakt of je de eerste u₀ of u₁ noemt. Dat deden we bij een rekenkundige rij ook al, weet je nog?

Oneindige Sommen

Het aparte aan zulke meetkundige rijen is, dat ook uit de som van een oneindig aantal termen soms toch een "gewoon"getal komt. Als namelijk de reden kleiner dan 1 is, dan worden de termen steeds kleiner, en dan zal bij oneindig veel termen de "volgende" term naar nul gaan.

Voorbeeld.
Dit is een hele beroemde meetkundige rij: 1 + ¹/₂ + ¹/₄ + ¹/₈ + .....
In het plaatje hiernaast zie je al dat hier 2 uitkomt! Leuk hè? Oneindig veel getallen die samen toch gewoon 2 opleveren.
Ook met onze somformule kun je dat zien: eerste = 1, reden = 0,5 en volgende = 0
Dat geeft S_∞= ^{(0 - 1)}/_{(0,5 - 1)}= 2

OPGAVEN

Bereken de volgende sommen:

1 + 3 + 9 + 27 + 81 + ... + 19683

29524

1024 + 1536 + 2304 + 3456 + ... + 17496

50440

10000 + 8000 + 6400 + 5120 + ... + 2097,152

41611,392

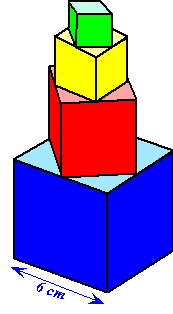
Hiernaast staat een stapel kubussen. De ribben van de onderste kubus zijn 6 cm. Vier hoekpunten van de tweede kubus vallen samen met de middens van de bovenste ribben van de eerste kubus. Op deze manier zijn 4 kubussen getekend. In gedachten zou je hiermee steeds door kunnen gaan

De ribben van de opeenvolgende kubussen vormen een meetkundige rij. Bereken de reden r.

0,5√2

Bereken de hoogte van de onderste 10 kubussen samen. Geef je antwoord in twee decimalen nauwkeurig

19,85

Hoe lang je ook door zou gaan met stapelen, de hoogte van de hele stapel komt nooit boven een bepaalde grenswaarde G.

Bereken deze G.

12+6√2

Bereken ook de grenswaarde voor de inhoud van de hele stapel.
rond je antwoord af op twee decimalen.

334,13

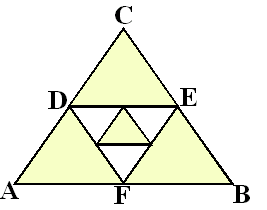
Hiernaast zie je een gelijkzijdige driehoek ABC met zijde 6 cm. Door de middens van de zijden met elkaar te verbinden ontstaat de gelijkzijdige driehoek DEF. Door de middens van de zijden van DEF te verbonden ontstaat weer een driehoek, enz.

Bereken de totale omtrek van de eerste 10 driehoeken samen. Geef je antwoord in twee decimalen nauwkeurig

35,96

Bereken de omtrek van alle driehoeken samen als je alsmaar door zou gaan.

Een professionele schilder wil wel eens wat anders. Hij besluit een wiskundig kunstwerk te gaan maken.
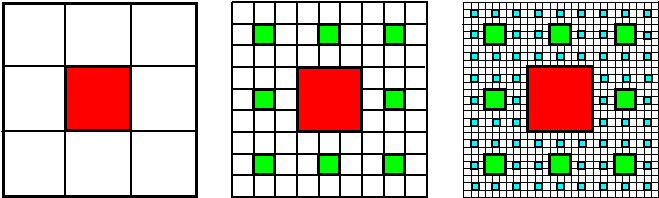
Hij verdeelt een vierkant doek van 3 bij 3 meter in negen kleinere vierkanten, en verft het middelste daarvan rood
Daarna verdeelt hij de 8 overgebleven vierkanten elk weer in negen vierkanten. Deze keer verft hij de middelste vierkanten groen.

De overgebleven vierkanten worden weer in negen delen verdeeld, en elke middelste wordt nu blauw.
Dit proces gaat zo alsmaar door totdat de schilder voor het eerst meer dan de 90% van de oppervlakte van het oorspronkelijke doek heeft gekleurd. Voor elke nieuwe serie vierkanten gebruikt hij een nieuwe kleur.
De totale oppervlakte die na n keer is gekleurd is dan gelijk aan 1 + ⁸/₉ + (⁸/₉)² + ...+ (⁸/₉)^n-1

Toon dat aan.

Hoeveel verschillende kleuren heeft hij dan gebruikt?

Hoeveel vierkanten heeft hij in totaal gekleurd? Rond je antwoord af.
Gaat zijn plan wel lukken?

2 • 10¹⁶

Iemand laat een bal vallen vanaf 80 cm hoogte. De bal stuitert en komt elke volgende keer tot 85% van de vorige hoogte. Hoeveel cm heeft de bal afgelegd als hij is uitgestuiterd?

533¹/₃ cm

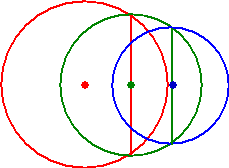
Je begint met een cirkel met straal 10. (rood)
Teken in die cirkel een verticale koorde.
Teken met die koorde als middellijn een nieuwe cirkel. (groen)
Teken in die nieuwe cirkel weer een verticale koorde.
Teken met die koorde als middellijn weer een nieuwe cirkel. (blauw)
Zie de figuur hiernaast.

Teken op deze manier 10 cirkels.
Wat zou de maximale afstand tussen het middelpunt van de eerste en van de tiende cirkel zijn?

Om de maximale afstand te bereiken moet je elk volgend middelpunt M_n+1op een vaste afstand cr_nvan het vorige middelpunt M_n kiezen. Waarbij r_nde straal van cirkel n is, en c een constante kleiner dan 1.

Leg uit waarom dat zo is.

Toon aan dat r_n_{+ 1} = √(1 - c² ) • r_n

Stel een formule op voor de afstand van middelpunt 1 tot middelpunt 10 en bepaal met je GR de maximaal te behalen afstand.

25,5985...

In een groot bos heerst een konijnenplaag. De boswachter schat dat er op het moment zo'n 15000 konijnen in zijn bos zitten. Hij gaat elke dag een uur lang konijnen afschieten. De eerste dag zijn dat er maar liefst 640, maar in de volgende dagen wordt dat snel minder (omdat er dan minder konijnen zijn natuurlijk). Het blijkt dat het aantal konijnen dat hij in een uur schiet elke dag 80% is van het aantal van de vorige dag.
Neem voor het gemak in deze opgave aan dat het aantal konijnen niet geheel hoeft te zijn, en dat er geen konijnen bijkomen of op een andere manier doodgaan.

Op welke dag schiet hij voor het eerst minder dan 80 konijnen?

dag 11

Hoeveel konijnen schiet hij in totaal in de eerste 15 dagen?

3087

Na hoeveel dagen zijn er minder dan 11900 konijnen in het bos aanwezig?

dag 18

Hoeveel konijnen zullen er uiteindelijk in het bos overblijven?

11800

Een heimachine slaat een betonnen paal de grond in. Bij de eerste klap gaat de paal 180 cm de grond in. Bij elke volgende klap gaat de paal 20% minder de grond in dan bij de vorige.
Hoe ver kan de heimachine een paal maximaal de grond in slaan?

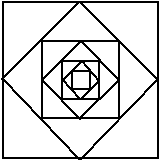
900 cm

Ik teken een vierkant van 16 bij 16 cm. Dit noem ik vierkant 1 (v₁). Daarna teken ik een tweede vierkant door de middens van de aanliggende zijden van v₁ met elkaar te verbinden. Dat levert me vierkant 2 (v₂). Dit proces herhaal ik een aantal keer, en zo krijg ik een groot aantal vierkanten in elkaar (zie figuur)

Laat zien dat voor de omtrek (u_n) van vierkant n de volgende recursieformule geldt: u_n+₁ = √2 • u_n

Geef een directe formule voor de rij u_n en bereken vervolgens voor welke n de omtrek van vierkant v_n voor het eerst kleiner zou zijn dan 0,0001 cm.

Als ik oneindig lang door zou gaan, hoe groot wordt dan de totale lengte van alle lijnstukken die ik teken samen?