|
|||||
| 1. | a. | 1 + 3 + 9 + 27 + 81 + ... + 19683
is meetkundig met r = 3 en de volgende is 59049 S = (59049 - 1)/(3 - 1) = 29524 |
|||
| b. | 1024 + 1536 + 2304 + 3456 + ... + 17496
is meetkundig met r = 1,5 en de volgende is 26244 S = (26244 - 1024)/(1,5 - 1) = 50440 |
||||
| c. | 10000 + 8000 + 6400 + 5120 + ... + 2097,152
is meetkundig met r = 0,8 en de volgende is 1677,7216 S = (1677,7216 - 10000)/(0,8 - 1) = 41611,392 |
||||
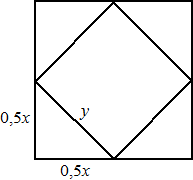
| 2. | a. | Als een kubus ribben x
heeft, dan geldt voor de ribben van de kubus erboven (zie de
figuur): y2 = (0,5x)2 + (0,5x)2
y2 = 0,25x2 + 0,25x2 y2 = 0,5x2 y = √0,5 x De reden r van de rij is dus √0,5 |
 |
||
| b. | De rij is
6 - 6 √0,5 - 6 (√0,5)2
- 6 (√0,5)3 - .... - 6
(√0,5)9 De volgende is 6 (√0,5)10 De som is (6 (√0,5)10 - 6)/(√0,5 - 1) = 19,84 cm |
||||
| c. | Bij een steeds grotere rij gaat
de hoogte van de volgende naar nul. S = (0 - 6)/(√0,5 - 1) = 6/(1 - √0,5) ≈ 20,485 |
||||
| d. | Als de ribbenlengte
met W0,5 wordt vermenigvuldigd, dan wordt de inhoud met (√0,5)3
= √0,125 vermenigvuldigd. De eerste inhoud is 63 = 216 De rij met inhouden is dan 216 - 216 √0,125 - 216 (√0,125)2 - ...... De volgende in een steeds grotere rij gaat weer naar nul. S = (0 - 216)/(√0,125 - 1) ≈ 334,13 |
||||
| 3. | a. | De zijden van een
driehoek zijn steeds gelijk aan de helft van de zijden van de vorige
driehoek. Dat geeft de rij omtrekken: 18 - 9 - 4,5 - 2,25 - .... - 18 0,59 De volgende is 18 0,510 S = (18 0,510 - 18)/(0,5 - 1) ≈ 35,96 |
|||
| b. | Als je alsmaar doorgaat wordt de
volgende gelijk aan nul. S = (0 - 18)/(0,5 - 1) = 36 |
||||
| 4. | a. | Elk nieuwe kleur
vierkantje heeft oppervlakte 1/9
van de vorige. Er zijn 8 keer zoveel nieuwe vierkantjes als de vorige Dus de nieuwe oppervlakte is 8 1/9 van de vorige Dat geeft een meetkundige rij met beginwaarde 1 en reden 8/9 De totaal geverfde oppervlakte is de som van die rij. |
|||
| b. | 90% van het
doek is oppervlakte 0,90 9 = 8,1 m2 S = ((8/9)^n - 1)/(8/9 - 1) = 8,1 (8/9)n - 1 = -0,9 (8/9)n = 0,1 Y1 = (8/9)^X Kijk bij TABLE wanneer dat voor het eerst minder dan 0,1 is, dat is bij n = 20 Hij moet 20 kleuren verf gebruiken. |
||||
| c. | De aantallen
vierkanten die hij verft met 20 kleuren zijn: 1 - 8 -
64 - .... - 819 Dat is een meetkundige rij met r = 8 en de volgende is 820 S = (820 - 1)/(8 - 1) = 1,65 1017 Als elk vierkant een seconde zou duren, dan is dat meer dan 5.000.000.000 jaar achter elkaar doorverven. Dat zal wel niet lukken...... |
||||
| 5. | De rij wordt:
80 - 0,85 80 - 0,852 80 -
0,853 80 - ..... Dat is een meetkundige rij met reden 0,85. Als je alsmaar doorgaat, dan gaat de volgende naar nul. S = (0 - 80)/(0,85 - 1) = 5331/3 cm. (alhoewel natuurlijk volgens deze rij de bal nooit is uitgestuiterd!!) |
||||
| 6. | a. | Elke volgende figuur
is een verkleining van de vorige, dus is er gelijkvormig mee. Wat dan voor de eerste de ideale plaats van dat volgende middelpunt is, is voor de volgende precies zo wéér de ideale plaats. |
|||
| b. | Zie de figuur hiernaast. Pythagoras: rn2 = (crn)2 + rn + 12 rn2 = c2rn2 + rn + 12 rn2 - c2rn2 = rn + 12 rn2 ( 1 - c2 ) = rn + 12 rn √(1 - c2) = rn + 1 |
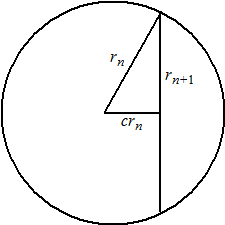 |
|||
| c. | de afstand is A =
cr1 + cr2 + .... + cr10
A = c (r1 + r2 + ... + r10) De r-waarden vormen een meetkundige rij met reden √(1 - c2) De volgende is r11 = 10 (√(1 - c2 )10 De som is (10 (√(1 - c2 )10 - 10)/(√(1 - c2) - 1) De afstand is dan 10 c ((1 - c2 )5 - 1)/(√(1 - c2) - 1) |
||||
| Invoeren n Y1 van de GR en dan calc - maximum geeft x = c = 0,4721 en afstand y = 28,56 | |||||
| 7. | a. | De aantallen
afgeschoten konijnen zijn: 640 - 640 0,8 - 640
0,82 - ....... Dat is een meetkundige rij met reden 0,8. mode - seq nMin = 1 un = u(n - 1) 0,8 u(nMin) = 640 TABLE en dan kijken wanneer dat voor het eerst minder dan 80 is: n = 11 |
|||
| b. | De volgende term (dag
16) is 640 0,815 = 22,52 S15 = (22,52 - 640)/(0,8 - 1) = 3087 konijnen |
||||
| c. | Er zijn minder dan
11900 konijnen als hij er in totaal minstens 3100 heeft
afgeschoten Sn = (640 0,8n - 640)/(0,8 - 1) Invoeren inY1 van de rekenmachine en dan bij TABLE kijken wanneer dat er meer dan 3100 zijn Dat is vanaf dag 16 |
||||
| d. | Soneindig
= (0 - 640)/(0,8 - 1) = 3200 Dan blijven er dus 15000 - 3200 = 11800 over. |
||||
| 8. | 20% minder betekent
nog 80% van de vorige slag. De afstanden zijn dan 180 - 180 0,8 - 180 0,82 - 180 0,83 - .... Dat is een meetkundige rijm met reden r = 0,8 Soneindig = (0 - 180)/(0,8 - 1) = 895 cm |
||||
| 9. | a. | Als een vierkant ribben x
heeft, dan geldt voor de zijden van het volgende vierkant: (zie de
figuur): y2 = (0,5x)2 + (0,5x)2
y2 = 0,25x2 + 0,25x2 y2 = 0,5x2 y = √0,5 x Als de zijden √0,5 keer zo groot worden, dan wordt de omtrek dat ook. De reden r van de rij is dus √0,5 = 1/2√2 Vandaar de gegeven recursievergelijking. |
 |
||
| b. | u1
= 4 16 = 64 u0 zou dan 64/√0,5 = √8192 zijn un = √8192 (0,5√2)n Y1 = √(8192) (0,5√(2))^X Kijk bij TABLE wanneer dat voor het eerst kleiner is dan 0,0001 is. Dat geeft n = 40 |
||||
| c. | Soneindig = (0 - 16)/(0,5√2 - 1) = 54,63 cm | ||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||