schoonvegen matrix


Schoonvegen.	© h.hofstede (h.hofstede@hogeland.nl)

stelsels vergelijkingen

Een stelsel van twee vergelijkingen is nog wel vrij eenvoudig op te lossen, maar als het aantal vergelijkingen (en dus ook het aantal onbekenden) groter wordt, dan wordt het oplossen erg snel onoverzichtelijk.
Er is een eenvoudige manier om de zaak toch overzichtelijk te houden en dat is de methode van het "schoonvegen van een matrix".
Een matrix is een manier om een stelsel van vergelijkingen op een handige manier te noteren.
Neem het volgende stelsel van drie vergelijkingen met drie onbekenden:

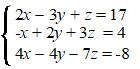Die "x", "y" en "z" en "=" overal staan er eigenlijk voor niks. Met de volgende notatie is het stelsel even goed duidelijk:

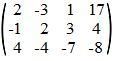We gaan deze matrix nu zodanig veranderen dat de oplossingen van ons stelsel direct af te lezen zijn. Daarbij moeten we alleen ervoor uitkijken dat we "dingen" met die matrix doen waarbij het stelsel geldig blijft.

Er zijn drie mogelijke dingen om met zo'n matrix te doen.

Ding 1: Rijen verwisselen.

Als je twee rijen van een matrix met elkaar verwisselt, dan is dat niets anders dan de vergelijkingen in een andere volgorde op te schrijven. Daarbij blijft het stelsel natuurlijk gelijk en dus de oplossingen ook.
De volgende drie matrices horen bij hetzelfde stelsel:

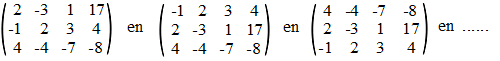Ding 2: Een rij met een constant getal vermenigvuldigen.

Als je een rij met een constant getal (niet nul!) vermenigvuldigt (of erdoor deelt, dat is natuurlijk hetzelfde) dan blijft de vergelijking waar die rij bij hoort gelden. 't Is eigenlijk de oude 'balansmethode' van heel vroeger.
De volgende drie matrices horen bij hetzelfde stelsel:

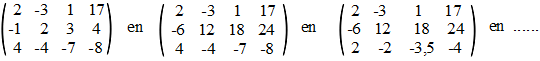Ding 3: Rijen bij elkaar optellen of van elkaar aftrekken.

In de les over twee stelsels met twee onbekenden hebben we al gezien dat je twee vergelijkingen ook wel bij elkaar op mag tellen. Dan krijg je een nieuwe vergelijking die óók geldig is. Immers als A = B en C = D dan geldt ook A + C = B + D.
De oude Griek Euclides hiernaast zei dat al.

(en van elkaar aftrekken mag natuurlijk ook: dat is hetzelfde als met min-één vermenigvuldigen en dan bij elkaar optellen)
Dat betekent dat de volgende drie stelsels gelijk zijn:

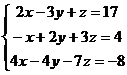In de eerste stap zijn de tweede en derde rij bij elkaar opgeteld en is de tweede rij daardoor vervangen.
In de tweede stap is de derde rij afgetrokken van de eerste en is de derde rij daardoor vervangen.
Denk erom dat de rij die je vervangt wel altijd één van de rijen is van het optellen/aftrekken.

Combinaties.

Natuurlijk kun je ook meerdere dingen tegelijk uitvoeren. Zo mag je best tweemaal de eerste rij nemen en dat optellen bij driemaal de tweede rij en het resultaat daarvan in rij 1 zetten.
Dat ziet er zó uit:

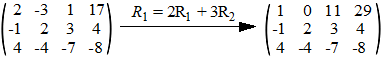Oké, wat moeten we daar nou mee?

Het wordt pas interessant als je jezelf beseft dat het stelsel vergelijkingen is opgelost als je matrix er zó uitziet:

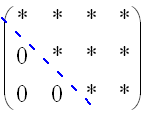Op die sterretjes mag alles staan, maar die drie nullen zijn essentieel! Zie je al waarom?
Als we de onbekenden weer even x, y en z noemen, dan staat er op de onderste rij ....z = ..... Dus z is opgelost.
Maar dan staat op de tweede rij ....y + ....z = ..... en als z bekend is, dan is y dat ook.
Maar met y en z bekend, geeft de bovenste rij x.
Zorgen dat daar linksonder allemaal nullen komen te staan heet het schoonvegen van de matrix. (Je kunt het ook Gauss-Jordan-eliminatie noemen als je geleerd wilt overkomen)

De volgende matrices zijn allemaal schoongeveegd:

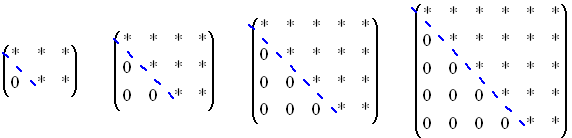(deze schoongeveegde vorm wordt ook wel de "bovendriehoeksvorm" of de "rij-echelon-vorm" genoemd; de definitie daarvan is: "elke volgende rij begint met meer nullen dan de vorige")

Laten we onze oorspronkelijke matrix gaan schoonvegen.

Die nullen kun je het best per kolom gaan maken.
En dat gaat het handigst als er in de bovenste kolom op de eerste plaats een 1 staat.
Vermenigvuldig daarom de tweede rij met -1 en verwissel hem met de eerste rij.

Dat geeft de matrix hiernaast.
Trek nu de eerste rij twee keer van de tweede af en vier keer van de derde.
Dat gaat lekker makkelijk met die 1 toch?
Je doet dus R₂ → R₂ - 2•R₁ en R₃ → R₃ - 4•R₁

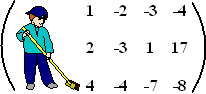Dat geeft de volgende matrix hiernaast.
De volgende stap is om van het getal in de tweede rij en tweede kolom ook een 1 te maken.
Maar wacht...mazzel! dat is al een 1!! Dus dat hoeft niet meer.
Met die 1 gaan we weer nullen naar beneden maken.
In de laatste rij kun je makkelijk een nul maken door viermaal de tweede rij af te trekken van de derde rij.

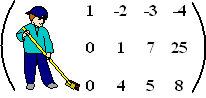Zoals hiernaast.

Daarmee is deze matrix schoongeveegd.
In de laatste rij staat nu -23z = -92 ofwel z = 4
In de tweede rij staat dan y + 28 = 25 ofwel y = -3
In de eerste rij staat dan x + 6 - 12 = -4 ofwel x = 2.

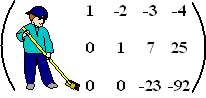Daarmee is het stelsel opgelost.

Samengevat doe je eigenlijk het volgende:

Maak de nullen per kolom, door steeds eerst het bovenste getal 1 te maken.

Met de Grafische Rekenmachine.

Je grafische rekenmachine kan een matrix ook schoonvegen.
Dat gaat zo:
Voer eerst je matrix in bij het menu 2ND MATRIX   EDIT   (eerst de afmetingen invoeren en daarna de elementen per rij)

Verlaat het menu (2ND quit)
Ga nu nar het menu 2ND   MATRIX MATH
en gebruik optie   A: ref(
Zet daar matrix A achter en je krijgt een schoongeveegde A als resultaat.

N.B.: er staat "een" schoongeveegde A want de schoongeveegde vorm (rij-echelon vorm) van matrix A is niet éénduidig bepaald. Je kunt immers best een bepaalde lagere rij nog een aantal keer bij een hogere optellen, dan blijft de matrix schoongeveegd.

OPGAVEN

Los de volgende stelsels vergelijkingen op door schoon te vegen:

2, -4, 1

-8, 3.5, 5

^-5/₂₂ , -⁴/₁₁, ¹²/₁₁

-2, 3, 7, -4

VEEG ZE!!!!

2,2,-3,4,1,6,5

Vlaamse Olympiade

Zack, Ziggy, Zules, Zork en Zoë zijn vierogige aliens.
Ze zitten in een cirkel en knijpen een aantal ogen toe.
Zack ziet nul ogen, Ziggy ziet 8 ogen, Zules ziet 6 ogen, Zork ziet 9 ogen en Zoë ziet 7 ogen.

Wie heeft exact drie ogen open?

Zoë