| |
 |
|
De Methode van de Verschillen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
| De methode van de verschillen is
helemaal gebaseerd op één, eigenlijk nogal simpele, observatie: |
| |
|
|
|
|
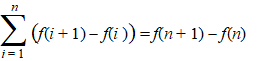 |
| |
|
|
|
Neem bijvoorbeeld n = 4,
dan staat aan de linkerkant: (f(2) - f(1)) + (f(3)
- f(2)) + (f(4) - f(3)) + (f(5) - f(4))
Maar als je de haakjes wegwerkt dan vallen alle termen twee aan twee
tegen elkaar weg en blijven alleen f(5) - f(1) over.
Laten we zien hoe deze eenvoudige regel het mogelijk maakt om de som
van een rij kwadraten te bepalen.
Stel dat je een formule wilt maken voor 12 + 22
+ 32 + ... + n2
De eerste slimme opmerking is dan, dat je kwadraten "ongeveer" kunt
schrijven als het verschil van derdemachten.
Kijk maar: (i + 1)3 - i3
= i3 + 3i2 + 3i + 1 - i3
= 3i2 + 3i + 1.
Neem daarom in bovenstaande simpele formule voor f de functie
i3, dan staat er: |
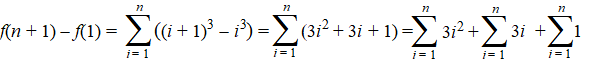 |
Van die drie laatste sommen zijn
er twee bekend: de laatste twee namelijk.
De laatste is natuurlijk gewoon n, en de middelste is een
rekenkundige rij, waarvan we al een formule voor de som hebben.
Maar de f(n + 1) - f(1) is natuurlijk
ook gewoon gelijk aan (n + 1)3 - 1 |
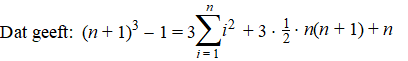 |
| Breng nu die
laatste twee termen aan de rechterkant ook naar links, dan heb je: |
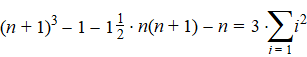 |
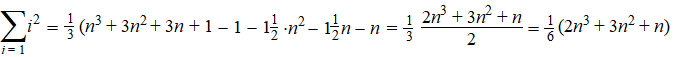 |
Dat laatste kun je nog wat
"mooier" schrijven als je daar zin in hebt:
1/6(2n3
+ 3n2 + n) = 1/6n(2n2
+ 3n + 1) = 1/6n(n
+ 1)(2n + 1). Dat geeft het prachtige resultaat: |
| |
|
|
|
|
|
| |
|
|
|
| 1. |
 |
| |
|
|
|
| |
a. |
Leid deze formule zelf af uit de
functie f(x) = x4. |
|
| |
|
|
|
| |
b. |
Leg uit waarom geldt:
(1 + 2 + 3 + ...+ 10)2 = 13 + 23 + ...
+ 103
Grappig toch? Dat de som van opvolgende derdemachten steeds een
kwadraat oplevert! |
| |
|
|
|
| |
c. |
Geef een formule voor
de eerste n termen in de rij: (12) + (12
+ 22) + (12 + 22 + 32) + (12
+ 22 + 32 + 42) ... |
| |
|
|
|
| 2. |
Voor een vreemde rij
un geldt dat de som van de eerste n termen
gelijk is aan
Sn = 1/2n5
+ 2n
Bereken u5 + u6 + u7 |
| |
|
|
|
| |
|
|
|
|
Telescoopsommen. |
| |
|
|
|
| Laten we beginnen met
een raadsel: |
| |
|
|
|
| |
De grote loterij duurt maar liefst tien
dagen.
De eerste dag is het nog simpel: er staat een vaas met twee
verschillende knikkers, die er uit gehaald gaan worden.
Iedereen die de volgorde goed voorspelt krijgt een goudstaaf.
Maar de tweede dag zitten er drie verschillende knikkers in de vaas. Om
nu de prijs te krijgen moet je de volgorde van die drie knikkers goed
voorspellen. Dat is natuurlijk moeilijker, maar de prijs is dan ook
groter: twee goudstaven.
De derde dag zijn er vier knikkers en is de prijs 3 goudstaven.
Dat gaat zo maar door.
Dus op de tiende en laatste dag zijn er 11 knikkers en is de prijs maar
liefst 10 goudstaven.
Hoeveel geld verwacht je te winnen als je elke dag meedoet? |
| |
|
|
|
De
oplossing;
Iedereen kan de verwachtingswaarde
wel uitrekenen natuurlijk. Neem bijvoorbeeld de zesde dag. Dan
zitten er 7 knikkers in de vaas. Die kunnen er op 7! (=5040)
manieren. De kans dat je de goede volgorde kiest is dus 1/7!
De prijs is op de zesde dag 6 goudstukken, dus de
verwachtingswaarde voor het te winnen bedrag de zesde dag
is 6/7! (≈
0,00119) goudstaaf.
Als we alle dagen bij elkaar optellen krijgen we voor het
te verwachten aantal goudstaven de volgende som:
|
| |
|
|
|
|
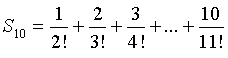 |
| |
|
|
|
| Laten we die stap
voor stap anders gaan schrijven: |
| |
|
|
|
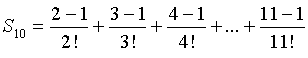 |
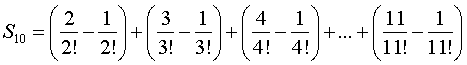 |
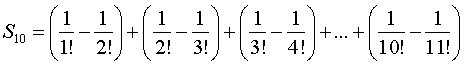 |
| |
|
|
|
En kijk eens aan: als je de
haakjes weglaat zie je dat bijna alles elkaar opheft. De tweede
en derde term, de vierde en vijfde term, de zesde en zevende
term enzovoort.
Het enige dat overblijft zijn de eerste en laatste term: |
| |
|
|
|
|
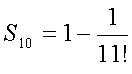 |
| |
|
|
|
De laatste som hierboven, die waarbij alle termen elkaar
opheffen, heet een telescoopsom
Immers hij schuift als het ware uit van de eerste
term naar de laatste, waarbij alle tussenliggende zó in
elkaar kunnen klappen: alleen de eerste en de laatste doen er
toe. De algemene vorm van een telescoopsom is: |
| |
|
|
|
|
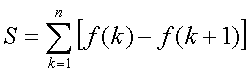 |
| |
|
|
|
| In dit voorbeeldgeval was trouwens f(k) = k/(k
+ 1)! |
| |
|
|
|
In feite hebben we
dat helemaal boven aan deze les bij die som van de kwadraten ook gedaan.
Als je namelijk op zoek zou gaan naar 12 + 22 + 32
+ .... + n2 dan ga je natuurlijk zoeken
naar een functie waarvoor geldt dat f(x + 1) - f(x)
= x2
Probeer je een derdegraadsfunctie f(x) = ax3 + bx2
+ cx + d dan levert dat al snel op dat a = 1/3 en
b = -1/2 en c =
1/6.
Conclusie: als f(x) = 1/3x3
- 1/2x2
+ 1/6 x dan
geldt f(n + 1) - f(1) =
12 + 22 + 32 + ... + n2
Dat geeft dan f(n + 1) - f(1) =
1/3(n
+ 1)3 - 1/2(n
+ 1)2 + 1/6 (n
+ 1) - 0 = ..... = 1/3n3
+ 1/2n2
+ 1/6n
En dat is (uiteraard) precies het resultaat dat we eerder al
vonden. |
| |
|
|
|
| |
|
|
|
| |
|
|
|
| 3. |
Op oudejaarsdag is het tijd voor goede
voornemens.....
Ik nummer daarom de dagen van
het komende jaar 1 tm 365
Ik ga een computer elke dag vragen willekeurig twee dagnummers
te trekken uit de dagen die al zijn geweest
Ik begin daarmee op dag 3 (dus op 3 januari) en eindig op dag
365 (31 december)
Elke keer als de computer precies eerst "dag
1" en daarna "dag 2" kiest, dan
geef ik €100 aan een goed
doel.
Hoeveel geld zal dat goede doel gemiddeld krijgen? |
| |
|
|
|
| |
a. |
Schrijf een uitdrukking voor dit
bedrag op. |
| |
|
|
|
| |
Je kunt dit bedrag berekenen met een
telescoopsom als je je bedenkt dat 1/n(n
+ 1) = 1/n - 1/(n
+ 1) |
| |
|
|
|
| |
b. |
Bereken op deze manier het verwachte
bedrag. |
| |
|
|
|
| |
|
|
|
| 4. |
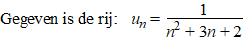 |
| |
|
|
|
| |
a. |
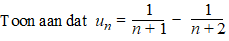 |
| |
|
|
|
| |
b. |
Geef een formule voor de som Sn
als de eerste term uit de rij n = 0 is |
| |
|
|
|
| 5. |
a. |
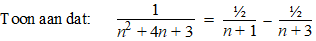 |
| |
|
|
|
| |
b. |
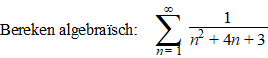 |
| |
|
|
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
| |
|
|
|