Gekoppelde rijen.

© h.hofstede (h.hofstede@hogeland.nl)
   
In de kantine van een groot bedrijf zijn elke dag twee maaltijden te krijgen:  een vegetarische maaltijd en een  vleesmaaltijd.
Een vaste groep van 650 mensen neemt elke dag zo'n maaltijd.
Het blijkt dat van degenen die op een dag vegetarisch eten 85% de volgende dag wéér vegetarisch eet, en dat 15% switcht naar een vleesmaaltijd.
Van de vleeseters op een dag neemt  70% de volgende dag wéér vlees, en 30% gaat over naar vegetarisch.

Als je het aantal vegetarische maaltijden op een dag V(t) noemt, dan hangt dat aantal niet alleen af van het aantal de vorige dag, maar óók van het aantal vleesmaaltijden van de vorige dag. En omgekeerd hangt het aantal vleesmaaltijden N(t) op een dag af van het aantal de vorige dag én van het aantal vegetarische maaltijden de vorige dag. 
De volgende twee vergelijkingen beschrijven dit systeem:  
   
Nt = 0,70Nt - 1 + 0,15Vt - 1
Vt = 0,85Vt - 1 + 0,30Nt - 1
   
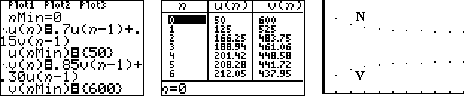
Dit heet een stelsel gekoppelde differentievergelijkingen, en ook die kun je natuurlijk makkelijk in de GR invoeren.
Gebruik MODE -  seq  en voer bij  Y=  de beide formules hierboven in.
Hieronder is dat gebeurd voor  N(0) = 600  en  V(0) = 50.
   

   
(in dit voorbeeld is voor het gemak aangenomen dat de aantallen niet geheel hoeven te zijn)
Rechts zie je hoe de grafieken van N(t) en V(t) er uitzien.
   
Evenwicht.

Het lijkt er in het bovenstaande voorbeeld op, dat de aantallen N en V al vrij snel op een stabiele waarde terechtkomen.
Die evenwichtswaarden kun je natuurlijk gemakkelijk berekenen, door te stellen dat dan moet gelden  Nt = Nt - 1 
en  Vt = Vt - 1. Immers dan veranderen de hoeveelheden niet.
Noem die evenwichtswaarden N en V,  dan geven de vergelijkingen van het voorbeeld:  
N = 0,70N + 0,15V  en  V =  0,85V + 0,30N

"Ha, een stelsel van twee vergelijkingen met twee onbekenden, dat kan ik makkelijk oplossen"  hoor ik je al denken. Maar dat valt hier vies tegen; beide vergelijkingen geven namelijk hetzelfde:  2N = V.

Gesloten systemen.

Gelukkig is er nog een derde voorwaarde, en dat is dat het totaal aantal maaltijdgebruikers in ons systeem constant is, namelijk 650. Er komen geen mensen bij en er gaan geen mensen van af. Dat kon je natuurlijk al wel zien aan die 30%-70% en 85%-15% helemaal aan het begin. Samen beide 100%......
Zo'n systeem heet een gesloten systeem.
Dat geeft een extra vergelijking  N + V = 650.
Samen met 2N = V  komen we dan op  3N = 650  ofwel  N ≈ 217 en  V ≈ 433.

Een directe vergelijking.

Zo'n gesloten systeem maakt het ook erg eenvoudig om een directe vergelijking voor N en V te maken.
Omdat  Nt - 1 + Vt - 1 = 650  geldt  Vt - 1 = 650 - Nt - 1
Invullen in de bovenste vergelijking van ons stelsel geeft  Nt = 0,70Nt - 1 + 0,15 • (650 - Nt - 1)
dat geeft Nt =  0,55Nt - 1 + 97,5
En dat is een oude bekende: een lineaire recursievergelijking, en die hebben we in deze les al behandeld.
Daar was de conclusie:

 

 

E was de evenwichtswaarde.
In dit geval geeft dat de oplossing:  Nt = 3831/3 • 0,55t + 2162/3
   
OPEN SYSTEMEN.
   
In een visvijver bevindt zich een populatie karpers.
We onderscheiden twee soorten karpers:  Jongen (0-1 jaar) en Volwassenen (meer dan 1 jaar). Door het vissen en door natuurlijke sterfte verdwijnt elk jaar 60% van de jonge en van de volwassen karpers. De volwassen karpers krijgen wel nakomelingen:  per karper gemiddeld 0,3 nakomelingen in een jaar.
Verder zet de hengelsportvereniging die de vijver beheert elk jaar 150 nieuwe jonge karpers uit.
Daarmee voldoen de aantallen karpers aan de volgende vergelijkingen:
   
Jt  =  0,3Vt - 1 + 150
Vt  =  0,40Vt - 1 + 0,40Jt -1
   
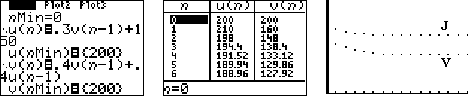
Dit is een open systeem omdat het totaal aantal karpers niet steeds hetzelfde hoeft te zijn. Er verdwijnen karpers uit het systeem en er komen van buiten nieuwen bij.
Stel dat we beginnen met een populatie van 200 volwassen karpers en 200 jonge karpers. Dan geeft onze GR het volgende:
   

   
Ook hier lijken de aantallen Jongen en Volwassenen naar een evenwichtswaarde te lopen. Die is natuurlijk eenvoudig uit de vergelijkingen te berekenen:   J = 0,3V + 150  en   V = 0,4V + 0,4J  geeft als oplossing  V = 125 en J ≈ 188
Let op het verschil met een gesloten systeem:  hier volgen de evenwichtswaarden direct uit de twee vergelijkingen. (Bij een open systeem waren de twee vergelijkingen niet op te lossen maar hadden we een extra derde voorwaarde dat het totaal constant moest zijn).
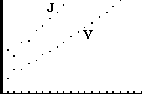
Het is overigens niet gegarandeerd dat zo'n theoretisch evenwicht ook werkelijk bereikt wordt. Als je bijvoorbeeld de 0,3 nakomelingen verandert in 1,6 dan nemen de aantallen karpers steeds meer toe, zoals je hiernaast ziet. 

(in dit geval is de wiskundige evenwichtssituatie:  V = -1500 en J = -2250 en dat is natuurlijk geen reële situatie)

   
   
  OPGAVEN
   
Bij al de volgende opgaven hoef je er geen rekening mee te houden dat aantallen gehele getallen moeten zijn.
   
1. Onder de bevolking (10000 mensen) van een eiland is een merkwaardige ziekte uitgebroken die zich kenmerkt door de volgende gegevens:
  • Elke week wordt 20% van de gezonde mensen ziek, de rest blijft gezond.
  • Van de zieke mensen geneest in een week 30% en blijft 70% ziek.
       
  a. Stel een stelsel differentievergelijkingen op dat de aantallen zieken (Z) en gezonden (G) beschrijft.
       
  b. Als nu van de bevolking 1000 mensen ziek is en 9000 gezond, hoe zal dat dan over 8 weken zijn?
     

6012 en 3988
  c. Hoe zal de evenwichtssituatie van deze 10000 mensen worden?
     

6000 en 4000
  d. Stel een directe formule op voor  G(t) als  G0 = 9000
       
2. Van een zware tweejarige particuliere opleiding zijn de volgende gegevens bekend:
  • 60% van de eerstejaars gaat over naar het tweede jaar, 20% gaat het eerste jaar overdoen en 20% verdwijnt van de opleiding
  • Van de tweedejaars haalt  70% het diploma, 20% gaat het tweede jaar overdoen en 10% verdwijnt van de opleiding 
  • In totaal is er plaats voor 1400 studenten, dus elk jaar neemt men zoveel nieuwe eerstejaars aan als er plek is (er is altijd een wachtlijst).
  Voor het aantal eerstejaars(E) en het aantal tweedejaars (T) studenten gelden dan de volgende vergelijkingen:
       
 
Et = 1400 - 0,2Tt - 1 - 0,6Et - 1
Tt = 0,2Tt - 1 + 0,6Et - 1
       
  a. Toon aan dat deze vergelijkingen gelden.
       
  Op dit moment zijn er 1200 eerstejaars en 200 tweedejaars.
       
  b. Onderzoek hoe de situatie over 6 jaar zal zijn
     

802 en 598
  c. Bereken algebraïsch hoe de evenwichtssituatie zal zijn.  
     

800 en 600
  d. Stel een derde differentievergelijking op voor het totaal aantal afgestudeerden vanaf nu (met een diploma) dat deze opleiding in totaal zal hebben afgeleverd, en bepaal met je GR wanneer dat voor het eerst meer dan 3000 zal zijn
     

n = 8
       
3. VN secretaris Generaal Ban Ki-Moon had het een aantal jaar geleden niet makkelijk om de twee aartsvijanden Bush (de president van Amerika) en Talabani (de president van Irak) dichter tot elkaar te brengen. Maar na lang piekeren had hij, met zijn kennis van gekoppelde differentievergelijkingen een oplossing gevonden. Het gaat naar Talabani en Bush met het volgende voorstel:
   
  Irak brengt elk jaar de uitgaven aan defensie terug tot 60% van de uitgaven van het jaar ervoor (dus vermindering van 40%). Maar om Amerika aan te moedigen ook te ontwapenen mag Irak vervolgens de uitgaven weer vermeerderen met 45% van het budget van Amerika het jaar ervoor. Amerika zal hetzelfde doen met de percentages 55% (overhouden van eigen budget) en 40% (van het budget van Irak erbij)
       
  Op dit moment geldt  A0 = 2500 en I0 = 500
       
  a. Stel een stelsel differentievergelijkingen op die dit systeem beschrijven. Leg daarna duidelijk uit hoe je aan dit stelsel kunt zien dat het hier een gesloten systeem betreft, en bereken de evenwichtswaarden.
     

1412 en 1588
  Natuurlijk gingen Talabani en Bush niet direct akkoord. Na lang onderhandelen werd besloten tot het volgende stelsel vergelijkingen:
   
An = 0,7An - 1 + 0,6In - 1
In = 0,4In - 1 + 0,3An - 1 + 100
met  A0 = 2500 en I0 = 500
       
  A = budget van Amerika, I = budget van Iran en alle bedragen zijn in miljoenen.
       
  b. Hoe groot zullen de uitgaven van Amerika en Irak  op n = 10 zijn?  
     

2593 en 1407
  c. Onderzoek of er een evenwichtssituatie zal ontstaan. Doe dat zowel met je GR als algebraïsch.
     

NEE
  Voor de wereldvrede zou het echter veel beter zijn om het volgende systeem te gebruiken:
       
   
An = 0,57An -1 + 0,76In - 1
In = 0,19In - 1 + 0,38An - 1
met  A0 = 2500 en I0 = 500
       
  Met deze vergelijkingen zal het totale wapenbudget van beide landen samen (A + I) elk jaar met 5% afnemen.
       
  d. Toon dat algebraïsch aan.  
       
4. De driedagsvlieg is een insect dat drie dagen leeft. We beschouwen van een populatie vliegen daarom ééndagige vliegen (E)  tweedagige vliegen (T) en driedagige vliegen (D)
De volgende gegevens zijn bekend:
  • elke tweedagige brengt gemiddeld één jong voort.
  • elke driedagige brengt gemiddeld 0,6 jong voort.
  • ééndagigen hebben 50% kans om de dag te overleven en tweedagige te worden
  • tweedagigen hebben 40% kans om de dag te overleven en driedagige te worden.
       
  Op dit moment (dag 0)  zijn er  van elke soort 2000 exemplaren
       
  a. Stel een stelsel van drie recursievergelijkingen op en onderzoek met je GR hoe de aantallen over 10 dagen zullen zijn.
     

321 - 197 - 100
  Zoals je bij a) hebt gezien sterft de populatie uit. Door het aantal jongen van 0,6 hoger te maken kun je ervoor zorgen dat de populatie niet uitsterft.
     
  b. Onderzoek hoe groot (één decimaal nauwkeurig) het aantal jongen dat een driejarige gemiddeld voortbrengt moet worden om ervoor te zorgen dat de vliegenpopulatie niet uitsterft.
     

  2,5 

       
5. Een reclamebureau onderzoekt welke soort cola er gedronken wordt door een grote testgroep van 3500 consumenten.  Men kijkt gedurende langere tijd naar het gebruik van de soorten Coca-Cola en Pepsi Cola, en komt tot het volgende model:

 C(t) = 0,85C(t – 1) + 0,12P(t - 1)
P(t) = 0,10C(t - 1) + 0,82P(t - 1)

C is het aantal Coca-Cola drinkers, P het aantal Pepsi-Cola drinkers en t de tijd in maanden.
In het begin geldt  C(0) = 1200 en P(0) = 1800

Voor deze opgave hoef je er geen rekening mee te houden dat het aantal mensen geheel moet zijn.

Het aantal mensen dat geen van deze twee merken drinkt neemt in de loop van de tijd toe.
       
  a. Leg uit hoe je dat direct aan deze vergelijkingen kunt zien.
       
  b.  Bereken na hoeveel maanden het aantal mensen dat geen van beide merken drinkt voor het eerst meer dan 80% van de groep is.
     

29 maanden
  c. Schets de grafiek met C op de x-as en P op de y-as voor de maanden 0 tm 100.
       
       
     

© h.hofstede (h.hofstede@hogeland.nl)