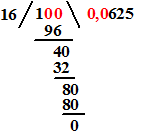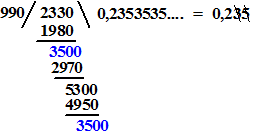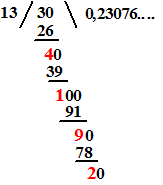repeterende breuken


Repeterende breuken.	© h.hofstede (h.hofstede@hogeland.nl)

ontbinden in factoren

Toen wij (ergens op de basisschool) voor 't eerst over breuken te horen kregen, schreven we die dingen als een deling van twee gehele getallen ^t/_n (t van teller, n van noemer).
Later (nog steeds op de basisschool trouwens) ontdekten we dat we die deling ook gewoon kunnen uitvoeren, namelijk met een staartdeling. Dat levert getal met cijfers achter de komma op; en decimale breuk.
Bijvoorbeeld, ¹/₁₆ rekenen we uit als:

En zo is duidelijk dat ¹/₁₆ te schrijven is als 0,0625.
Wat kon daaraan misgaan? Nou eigenlijk niets.
Soms kreeg je wel een grappig verschijnsel, bijvoorbeeld bij ²³³/₉₉₀ hiernaast. Die blauwe 3500 gaat zich herhalen. Dus de hele breuk gaat zich steeds maar weer herhalen. Daar komt geen eind aan.
Zo'n breuk noemen we repeterend.
Je kunt dat aangeven door een streepje door het eerste en het laatste cijfer van het repeterende stuk te zetten, zoals in de figuur helemaal rechts is gebeurd.

Omdat dat op een toetsenbord niet zo makkelijk gaat, zal ik in de rest van deze les dat stuk tussen vierkante haken zetten, dus ²³³/₉₉₀ = 0,2[35]. De allersimpelste repeterende breuk is natuurlijk ¹/₃ = 0,[3].

Kan een breuk alsmaar doorgaan en niet repeteren?

Goeie vraag (als zeg ik het zelf).

Het antwoord is NEE, dat kan niet.
Dat kun je eenvoudig inzien door naar de resten te kijken.
Hiernaast zie je die resten voor de breuk ³/₁₃. Het zijn de rode getallen 4, 1, 9, 2 ... hiernaast).

Maar omdat zo'n rest altijd kleiner dan 13 moet zijn, zijn er maar 12 mogelijke getallen als rest te krijgen. Dus de breuk moet zich zeker gaan herhalen, hoogstens na 12 keer.
(het blijkt dat ³/₁₃ dat al eerder doet; het is 0,[230769] )

Welke breuken zijn repeterend en welke niet?

Op de eerste plaats hoop ik dat je inziet dat het repeteren of niet van een breuk alleen door de noemer van de breuk wordt bepaald. Je kunt de breuk ^t/_n natuurlijk gewoon schrijven als t · ¹/n en als een stuk (¹/_n) wel of niet repeteert, dan blijft dat zo als je vermenigvuldigt met een getal t. Daarom zal ik vanaf nu alleen breuken ¹/_n (zogenaamde stambreuken) bekijken.

Om te zien wanneer een breuk repeteert, kun je het best kijken naar wanneer een breuk NIET repeteert.
Neem bijvoorbeeld de breuk ¹/₈. Die repeteert niet, want ¹/₈ = 0,125
Vermenigvuldig met 1000 en je krijgt ¹⁰⁰⁰/₈ = 125. Dus 8 is een deler van 1000.

En zo is ¹/₃₂ = 0,03125 en als je dat met 100000 vermenigvuldigt krijg je ¹⁰⁰⁰⁰⁰/₃₂ = 3125.
Dus 32 is een deler van 100000.

Waar komt het op neer:

een breuk repeteert NIET als de noemer een deler is van een macht van 10

Hoe kun je zien of iets een deler is van een macht van 10? Er zijn zoveel machten van 10.....
Daar komt het ontbinden in priemfactoren handig van pas. (deze les)
Een macht van 10 is te schrijven als 10 • 10 • 10 • ..... = 2 • 5 • 2 • 5 • 2 • 5 • .....
Dus de priemfactorontbinding van zo'n macht bestaat alleen uit de priemgetallen 2 en 5.

Een getal dat daar deler van is mag dus ook alleen priemgetallen 2 en 5 in zijn factorontbinding hebben.

een breuk repeteert NIET als de priemfactorontbinding alleen 2^en en 5^en bevat

In alle andere gevallen repeteert een breuk WEL.

Daarmee hebben we ook meteen het aantal cijfers achter de komma van zo'n niet-repeterende breuk gevonden: kijk naar het aantal tweeën en het aantal vijven in de priemfactorontbinding en neem het grootste aantal van beiden.

Bepaal zonder de volgende breuken uit te rekenen of ze repeteren of niet. Geef van de niet-repeterende breuken het aantal cijfers achter de komma.

¹/₁₆₀

niet; 5

¹/₆₂₅

niet; 4

¹/₁₄₀

wel

¹/₇₅₀₀

wel

¹/₆₄

niet; 6

¹/₅₁₂₀

niet; 10

Hoe groot is het repeterende deel?

De lengte van dat repeterende deel noem ik vanaf nu de periode van de breuk.
Nou kunnen we op dezelfde manier als gebeurde bij niet-repeterende breuken ook van repeterende breuken de periode vaststellen.
Stel dat de breuk is: ¹/_n = 0,[a₁a₂a₃...a_p] dus dat de periode p is.
Vermenigvuldig met 10^p; dat geeft 10^p • ¹/_n = a₁a₂a₃...a_p,[a₁a₂a₃...a_p]
Trek daar het getal ¹/_n aan beide kanten van af, dan blijft er aan de rechterkant een geheel getal over:
10^p • ¹/_n - ¹/_n = a₁a₂a₃...a_p
⇒¹/_n• (10^p - 1) = a₁a₂a₃...a_p
Dat is een geheel getal, dus n is een deler van 10^p - 1.

De periodelengte is de kleinste p waarvoor geldt dat n een deler is van 10^{p - 1} .

Hier zie je een lijstje met periodelengtes:

p	10^p - 1	priemfactorontbinding	stambreuken met deze periode:
1	9	3 • 3	¹/₃, ¹/₉
2	99	3 • 3 • 11	¹/₁₁, ¹/₃₃, ¹/₉₉
3	999	3 • 3 • 3 • 37	¹/₂₇, ¹/₃₇, ¹/₃₃₃, ¹/₉₉₉
4	9999	3 • 3 • 11 • 101	¹/₁₀₁,¹/₃₀₃,
5	99999	3 • 3 • 11111	¹/₃₃₃₃₃^{, 1}/₉₉₉₉₉
6	999999	3 • 3 • 3 • 7 • 11 • 13 • 37	¹/₇, ¹/₁₃,¹/₂₁,¹/₃₉,¹/₆₃,¹/₇₇,¹/₉₁,¹/₁₁₁,¹/₁₁₇,¹/₁₄₃,¹/₂₃₁,¹/₂₅₉,¹/₂₇₃,¹/₂₉₇,¹/₃₅₁,¹/₄₀₇,¹/₄₂₉,¹/₄₈₁,¹/₇₇₇,¹/₈₁₉,¹/₁₀₀₁,¹/₁₂₂₁,¹/₁₂₈₇,¹/₂₀₇₉,¹/₂₃₃₁,¹/₂₄₅₇,¹/₂₈₄₉,¹/₃₃₆₇,¹/₃₆₆₃, ¹/₃₈₆₁,¹/₄₃₂₉,¹/₆₉₉₃,¹/₈₅₄₇,¹/₉₀₀₉,¹/₁₀₉₈₉,¹/₁₂₉₈₇,¹/₁₄₂₈₅₇,¹/₁₅₈₇₃, ¹/₂₅₆₄₁,¹/₄₇₆₁₉,¹/₇₆₉₂₃,¹/₉₉₉₉₉₉

Denk eraan dat je al deze breuken nog een willekeurig aantal keer met 2 of 5 kan vermenigvuldigen zonder de periode te veranderen.
Zo heeft ¹/₁₁ periode 2, dus ook ¹/₂₂, ¹/₄₄, ¹/₅₅, ¹/₂₇₅, ¹/₁₁₀, enz. hebben periode 2.

WOW; daar rechtsonder zie je dat er maar liefst 42 gevallen zijn met periode 6 (die heb ik gevonden door gewoon alle combinaties van één of meer priemgetallen getallen uit de priemfactorontbinding proberen, en te kijken of die breuk niet al hoger in de tabel staat).
Nou is dit wel een beetje een omslachtige manier om de periode van een breuk te vinden. Er zijn gelukkig een aantal trucs waarmee het sneller kan.

TRUC 1: Als n een priemgetal is, dan is de periode van ¹/_n een deler van n - 1
Voorbeeld: Daarmee weten we dan dat de periode van ¹/₁₇ een deler van 16 zal zijn, dus 1, 2, 4, 8 of 16. Gezien bovenstaand lijstje (daar zit geen 17 bij) moet het 16 of 8 zijn.
99999999 is niet deelbaar door 17 dus moet 9999999999999999 dat wél zijn.
Inderdaad is 9999999999999999 : 17 = 588235294117674
De periode van ¹/₁₇ is dus 16.

TRUC 2: Als n en m priemgetallen zijn en ¹/_n en ¹/_m hebben periodes p₁ en p₂, dan is de periode van ¹/_(nm)gelijk aan het kleinste gemene veelvoud van p₁ en p₂ of een veelvoud daarvan.
Voorbeeld: ¹/₅₈₉ = ¹/_{(19 • 31)}
de periode van ¹/₁₉ is een deler van 18, dus 1, 2, 3, 6, 9 of 18, en blijkt gelijk te zijn aan 18
de periode van ¹/₃₁ is een deler van 30, dus 1, 2, 3, 5, 6, 10, 15 of 30 en blijkt gelijk te zijn aan 15.
Het kgv van 15 en 18 is 90. Dus de periode van ¹/₅₈₀ zal gelijk zijn aan 90.

Voorbeeld: ¹/₁₁₉ = ¹/_{(7
• 17)}
de periode van ¹/₇ is 6 en de periode van ¹/₁₇ is 16.
het kgv van 6 en 16 = 48 dus de periode van ¹/₁₁₉ is 48.
inderdaad is ¹/₁₁₉ = 0,008403361344537815126050420168067226890756302521.

TRUC 3: Als n een priemgetal is, en de periode van ¹/_n is p, dan is de periode van ¹/_n2 gelijk aan np
Op deze truc zijn tot nu toe slechts drie uitzonderingen bekend, namelijk p = 3 en p = 487 en p = 56598313.
Voorbeeld: ¹/₁₆₉ = ¹/₁₃2. De periode van ¹/₁₃ is gelijk aan 6, dus de periode van ¹/₁₆₉ is gelijk aan 6•13 = 78
Grappig; dan weten we nu dus ook dat 10⁷⁸ - 1 deelbaar is door 169. COOL!!!!

Deze truc is nog verder uit te breiden.
Als n een priemgetal is en de periode van ¹/_n is p, dan is de periode van ¹/_nk gelijk aan p • n^{k - 1}
Weer met alleen de priemgetallen 3 en 487 als uitzondering.
Voorbeeld: ¹/₂₄₀₁ = ¹/₇4 . De periode van ¹/₇ is 6, dus de periode van ¹/₂₄₀₁ is gelijk aan 6 • 7³ = 2058.

TRUC 4: een combinatie van alle vorige trucs! Kijk maar hoe het werkt:
Stel dat we de periode van ¹/₄₀₃₂₉ willen weten.
de priemfactorontbinding ervan is 40329 = 3³ • 7² • 23 (mochten hier factoren 2 of 5 in staan dan halen we die er eerst uit; die beïnvloeden immers de periode niet. In dit geval is dat niet zo).
• ¹/₃ heeft periode 1.
• ¹/₃2 heeft ook periode 1 (de uitzondering bij truc 3!).
• ¹/₃3 heeft periode 1 • 3.
• ¹/₇ heeft periode 6.
• ¹/₇2 heeft periode 7 • 6 = 42.
• ¹/₂₃ heeft periode 22.
Dan hebben ¹/₃3 en ¹/₇2 en ¹/₂₃ samen een periode die gelijk is aan het kgv van 3, 42 en 22 en dat is 462.

Bereken de periode van de volgende breuken:

¹/₄₂₃₅

¹/₇₀₇

¹/₃₄₃

294

¹/₂₅₄₈

¹/₃₀₂₅

¹/_3470131

80850

Toon aan dat 10⁶⁶ - 1 deelbaar is door 847.

Toon aan dat 10⁴⁰⁴ - 1 deelbaar is door 10201.

Hoe maak je van een repeterende breuk een gewone breuk?

Dat is gelukkig vrij makkelijk.
Neem bijvoorbeeld de breuk 0,123123123123.... = 0,[123]
Stel die breuk gelijk aan B.
Dan is dus B = 0,123123123123....
Maar dan is 0,001B = 0,000123123123123....
Trek deze laatste twee vergelijkingen van elkaar af, dan valt die hele staart weg: 0,999B = 0,123
Daaruit volgt dat B = ^0,123/_0,999= ¹²³/₉₉₉en dat is nog te vereenvoudigen tot ⁴¹/₃₃₃Omdat de periode gelijk was aan 3 vermenigvuldigden we B natuurlijk met 10^-3 = 0,001, dat snap je hopelijk wel.

(opmerking: je kunt zo'n breuk ook zien als som van een meetkundige rij: 0,[123] = 123 • 10^-3 + 123 • 10^-6 + .... en dan kun je met de formule voor de som van zo'n rij B uitrekenen. Dat staat in deze les)

Dit werkt natuurlijk ook bij een combinatie van repeterend en niet repeterend.
Neem de breuk 0,124545454545.... = 0,12[45]
Het repeterende deelheeft periode 2, dus vermenigvuldig met 0,01; dat geeft 0,00124545454545...
Trek 0,01B van B af: 0,99B = 0,1233 dus B = ¹²³³/₉₉₀₀ = ¹³⁷/₁₁₀₀

Schrijf de volgende repeterende breuken als gewone breuken ^t/_n:

0,144144144...

¹⁶/₁₁₁

0,8333333....

⁵/₆

0,223434343434...

⁵⁵³/₂₄₇₅

0,681818181...

¹⁵/₂₂

0,0112211221122...

⁵⁶/₄₉₉₅

0,396039603960...

⁴⁰/₁₀₁

Grapje tot slot.

Als je de breuk 0,999999.... op deze manier bekijkt, dan is die precies gelijk aan 1.
Niet ongeveer, maar exact!!! Dus 0,9999999.... is een geheel getal!!!

Kijk maar:
B = 0,99999....
0,1B = 0,0999999.....
Dus 0,9B = 0,9 ofwel B = 1

Je kon het ook zó zien: ¹/₉ = 0,11111.... dus 1 = ⁹/₉ = 9 • 0,11111.... = 0,99999....