|
|
 |
|
Raaklijnen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Een raaklijn is een
rechte lijn die een grafiek raakt.
Maar ja, daar schiet je natuurlijk nog niets mee op, want wat is nou
raken?
De volgende plaatjes maken misschien duidelijk wat daarmee wordt
bedoeld. |
| |
|
|
 |
| |
|
Je ziet één of andere groene
grafiek, met steeds een blauwe rechte lijn erbij getekend.
Eén van die plaatjes is speciaal!
Zie je welke?
Wiskundigen vinden plaatje nummer 5 een speciale. Daarin ligt die blauwe
lijn net "tegen de grafiek aan". Je zou ook kunnen zeggen dat de blauwe
lijn "precies langs" de grafiek loopt.
Zo'n lijn die "langs de grafiek loopt" of "ertegenaan ligt" heet een
raaklijn. |
| |
|
Nou is dat "er langs lopen" of
"er tegenaan liggen" natuurlijk niet netjes wiskundig gezegd. Je kunt
dat nauwkeuriger zo zeggen:
"Een raaklijn in een punt van een grafiek heeft
dezelfde helling als de grafiek in dat punt".
(Eerder hebben we al precies bekeken wat we bedoelen met de helling van
een grafiek in een punt). |
 |
Het punt waar de raaklijn de
grafiek raakt heet heel toepasselijk het raakpunt.
Let dus goed op je taalgebruik; er is een groot wiskundig verschil
tussen raken en snijden! |
| |
|
|
 |
| |
|
Rechts hierboven zie je dat één
lijn een grafiek zelfs zowel kan raken als snijden!
Een andere manier om het te zien.
Als je maar een héél klein stukje van een grafiek bekijkt, dan
is dat bij benadering ongeveer een recht lijntje. Als je er nog
kromming in ziet dan moet je gewoon een nóg kleiner stukje bekijken.
Dus op den duur, als je een héél, héél, héél, héél, hééééééél klein
stukje van een grafiek bekijkt dan is dat zo goed als een recht
lijntje.
Nou; de raaklijn is dat mini rechte lijntje, maar dan doorgetrokken. |
 |
| |
|
|
|
Hoe maak je de vergelijking van een
raaklijn? |
| |
|
Dat is gelukkig erg eenvoudig.
Je moet je op de eerste plaats bedenken dat een raaklijn een rechte lijn
is, dus de formule ervan zal er uitzien als y = ax+ b.
Die lijn is makkelijk te vinden, immers je weet dat de helling van
de raaklijn gelijk is aan de helling van de grafiek in het raakpunt. En
die laatste kun je vinden door de x van het raakpunt, xR,
in te vullen in de afgeleide functie f '. |
| |
| helling
raaklijn |
= |
helling grafiek |
| a |
= |
f '(xR) |
|
|
| |
|
| Om nu een raaklijn op te stellen
volg je de volgende drie stappen: |
| |
|
|
| STAP 1. |
|
| |
Bereken de coördinaten (xR,
yR) van het raakpunt. xR wordt meestal
gegeven, yR kun je berekenen door xR
in het functievoorschrift in te vullen. |
| |
|
|
| STAP 2. |
|
| |
Bereken de helling a van
de raaklijn: a = f ' (xR), dus je
vult xR in in de afgeleide functie f ' . |
| |
|
|
| STAP 3. |
|
| |
Bereken de b van de lijn
door het raakpunt (xR, yR) in te
vullen in y = ax + b. |
| |
|
|
Voorbeeld.
Gegeven is de functie f(x) = 3x3
-
2x + 1.
Geef de vergelijking van de raaklijn aan de grafiek van f in het
punt waarvoor x = 2.
Oplossing:
f(2) = 3 • 23 - 2 • 2 + 1 = 21 dus het raakpunt is
R(2, 21)
f ' (x) = 9x2 - 2, dus a =
f ' (2) = 9 • 22 - 2 = 34
y = ax + b geeft dan 21 = 34 • 2 + b
ofwel b = -47
De raaklijn is de lijn y = 34x - 47. |
| |
|
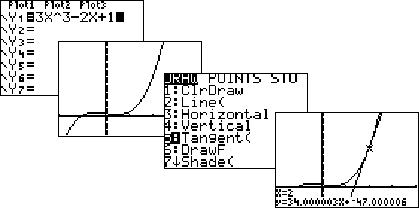
Met de TI-83
En ja, natuurlijk kan dit alles ook met de TI-83.
Zet het functievoorschrift in Y1
Plot de grafiek.
Toets dan in
2nd
DRAW
5: Tangent(
ENTER
Druk dan op
2
en onder in beeld verschijnt
X = 2.
Nogmaals
ENTER
en je krijgt de vergelijking van de raaklijn onder in beeld.
Hij tekent 'em zelfs voor je!! |
 |
| |
|
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Bereken algebraïsch de vergelijking van de
raaklijn aan de grafiek van f(x) in de
volgende gevallen: |
| |
|
|
|
| |
a. |
f(x) = 4x2
+ 2x - 6 bij x = -3. |
|
| |
b. |
f(x) = 4√x
- 5 bij x = 4. |
|
| |
c. |
f(x) = 4 - 6/x
bij x = -2. |
|
| |
d. |
f(x) = 3x4
- 5x2
+ 2x bij x = 1.
|
|
| |
e. |
f(x) = x2√x
bij x = 2. |
|
| |
|
|
|
| 2. |
De lijn y = 10x
+ p raakt de grafiek van f(x) =
6x - x2
Bereken algebraïsch de waarde van p |
| |
|
|
|
| |
|
| 3. |
Geven is de functie
f(x) = 1/x2
+ 2x2 √x +
4
Geef een vergelijking van de raaklijn in het punt (1,7) aan de
grafiek van f. |
| |
|
|
|
| |
|
|
|
| 4. |
Gegeven is de functie f(x)
= 2x3 - 6x2 + x
De grafiek van f heeft twee raaklijnen met
hellinggetal 49.
Bereken algebraïsch de verticale afstand tussen die twee
raaklijnen. |
| |
|
|
|
| |
|
|
|
| 5. |
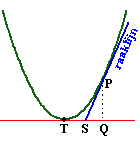
Ik ontdekte laatst een
grappige eigenschap van parabolen.
Stel dat je een raaklijn tekent door een punt P van een parabool
Stel dat je ook een horizontale lijn l tekent door de
top.
Stel dat je die raaklijn snijdt met lijn l en stel dat je
dat snijpunt S noemt.
Stel dat je vanuit P een verticale lijn snijdt l en dat
je dat snijpunt Q noemt.
Dan is S altijd het midden van TQ!
Grappig hé?
Bewijs deze uiterst vermakelijke eigenschap voor de parabool
y = x2 |
 |
| |
|
|
|
| 6. |
Bewijs dat de grafiek van f
(x) = x3 - 2x2
- 15x
+ 36 de x-as raakt. |
| |
|
|
|
| 7. |
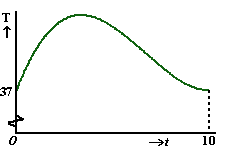
Een jongetje krijgt op
tijdstip t = 0 de griep. Als gevolg daarvan begint zijn
temperatuur meteen te stijgen. Voor deze soort griep geldt voor
de temperatuur T (in ºC) het model
T(t) = 0,02t3 - 0,4t2
+ 2t + 37
met t in dagen, en 0 ≤ t
≤ 10.
De grafiek van T(t) zie je hiernaast. |
 |
| |
|
|
| |
a. |
Met welke snelheid (ºC/dag) neemt de temperatuur
in het begin toe? |
| |
|
|
| |
|
|
|
| |
b. |
Het jongetje meet op
t = 4 hoe snel zijn temperatuur afneemt. Vervolgens berekent
hij hoe lang het zal duren totdat hij weer 37ºC is als die
afnamesnelheid zo zou blijven.
Maak die berekening. |
| |
|
|
|
| |
|
|
|
| 8. |
Alle grafieken van y
= xn gaan door het punt (1,1).
Als je de raaklijn in het punt (1,1) aan de grafiek van y
= xn tekent, dan snijdt die de y-as
bij y = 1 - n |
| |
|
|
|
| |
a. |
Toon dat aan. |
|
| |
|
|
|
| |
b. |
Waar snijdt deze raaklijn de x-as? |
|
| |
|
|
|
| |
|
|
|
| 9. |
examenvraagstuk HAVO Wiskunde B,
1993. |
| |
|
|
|
| |
In de figuur
hiernaast zijn drie bergparabolen getekend met raaklijnen in de
snijpunten A en B met de x-as. Deze raaklijnen snijden elkaar
in punt S op de y-as. In elke tekening lijkt het erop dat S
op een hoogte ligt die tweemaal zo groot is als de hoogte van top T.
Om de bewering: "S ligt tweemaal zo hoog als T" te
bewijzen gaan we uit van de parabolen met vergelijking:
y = -a(x2 - 1), met a
> 0Bewijs de bewering voor deze parabolen. |
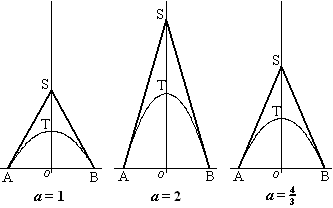 |
| |
|
|
|
| 10. |
Gegeven is de functie f(x)
= √(x + 8) |
| |
|
|
|
| |
a. |
Geef een vergelijking van de
raaklijn aan de grafiek van f in het punt waar x =
1 |
| |
|
|
|
| |
b. |
Benader met behulp van
deze raaklijn de waarde van √(9,03)
en kijk hoeveel procent deze waarde van de werkelijke waarde
verschilt. |
| |
|
|
|
 |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
| |
|
|
|
|