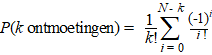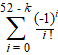© h.hofstede (h.hofstede@hogeland.nl)

Het Ontmoetingsprobleem
       
Stel dat je 100 kaarten hebt, genummerd van 1 tm 100. Die kaarten ga je eerst schudden, en daarna leg je ze één voor één op tafel. Daarbij roep je steeds hardop de hoeveelste kaart je neerlegt. (Je huisgenoten mompelen vast iets als "NERD" of zo, maar wij weten wel beter: het is gewoon een interessant wetenschappelijk experiment).
Elke keer als het nummer dat je roept gelijk is aan het nummer dat op de kaart die je neerlegt staat noemen we dat een ONTMOETING.

De kernvraag is:  Hoe groot is de kans op n ontmoetingen?  En hoe hangt die af van het aantal kaarten? (eerst 100, maar kan natuurlijk elk aantal N zijn....)

Laten we eenvoudig beginnen...

Stap 1:  één ontmoeting.

De kans dat de eerste kaart een ONTMOETING is, is uiteraard gelijk aan 1/100 (het moet nummer 1 zijn).
En nou komt de geniale (al zeg ik het zelf) gedachte:  de kans dat de 40e kaart een ontmoeting is, is ook 1/100!!!!

Waarom?
(teleurgesteld) Goh, jij bent duidelijk minder geniaal dan ik....
Kijk, als die kaarten goed geschud zijn, dan kun je net zo goed zeggen dat de eerste kaart die je neerlegt de 40e is. Wat maakt het uit hoe je hem noemt?
Elke kaart heeft vóór het schudden dezelfde kans om op de eerste plaats te komen als op de 40e plaats.
Als je liever een bewijs met getallen hebt moet je maar hiernaast kijken
     
Stap 2:  meer ontmoetingen.
       
De kans dat de eerste EN de tweede kaart ontmoetingen zijn is gelijk aan   1/100 • 1/99
En daar gaat íe weer:  de kans dat twee andere kaarten ontmoetingen zijn is dan ook gelijk aan  1/100 • 1/99.
Als je bijvoorbeeld de kans dat de 24e kaart EN de 76e kaart ontmoetingen zijn wilt uitrekenen, dan noem je de eerste twee kaarten die je neerlegt toch gewoon nummer 24 en nummer 76??  Wat maakt dat uit? Het is toch willekeurig?

Voor de echt achterdochtige mensen staat hiernaast ook daarvan nog een bewijs, maar hierna stop ik daarmee hoor!
     
De kans dat de eerste en de tweede en de derde en.... en de kde kaart allemaal ontmoetingen zijn is dan gelijk aan 
       
Dat kans dat er k ontmoetingen zijn, die willekeurig ergens mogen staan is dan  (N nCr k) keer zo groot, immers dat is het aantal manieren waarop k ontmoetingen verdeeld kunnen worden over N plaatsen. (Hierboven zagen we al dat al die verschillende verdelingen dezelfde kans hebben).
       
       
Maar daar mist nog iets......Dat brengt ons bij stap 3.
       
Stap 3:  De kans op 0 ontmoetingen.
       
Als er precies k ontmoetingen moeten zijn, dan moeten die andere N - k gevallen dus ook géén ontmoeting zijn:
De vraag wordt daarom:  "Wat is de kans dat er bij m kaarten geen enkele ontmoeting plaatsvindt?"
Dat hebben we al in een andere les behandeld! Namelijk de les waarin we de kans berekenden dat lootjes trekken lukt (dus dat er geen ontmoetingen zijn) Zie daarvoor deze les.
De conclusie daar was:
       
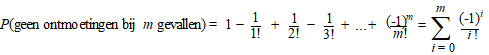Samengenomen geeft dat voor de kans op precies k ontmoetingen bij N experimenten:
       

       
Voorbeeld.

Twee personen zitten tegenover elkaar, elk met een standaarddeck met 52 speelkaarten. Ze draaien steeds tegelijk een kaart om, en gaan zo het hele deck door.
Hoe groot is de kans dat ze 0, 1, 2, ... keer precies tegelijk dezelfde kaart omdraaien?

Ik hoop dat je ziet dat het hier om een ontmoetingskans gaat.
Noem de kaarten waarop persoon A zijn deck doorloopt per definitie op volgorde nummer 1, 2, 3.... Dan gaat het om de kans dat persoon B bij beurt i ook kaart i omdraait.
Met bovenstaande formule maken we de volgende tabel:
       
aantal ontmoetingen k   kans op k ontmoetingen
0 0,3679 0,3679
1 0,3679 0,3679
2 0,3679 0,1839
3 0,3679 0,0613
4 0,3679 0,0153
5 0,3679 0,0053
6 0,3679 0,0005
... ... ...
46 0,3679 0,0000
47 0,3681 0,0000
48 0,3667 0,0000
49 0,3750 0,0000
50 0,3333 0,0000
51 0 0
52 1 0,0000
       
       

© h.hofstede (h.hofstede@hogeland.nl)