tussenwaardestelling


© h.hofstede (h.hofstede@hogeland.nl)
De Tussenwaardestelling. - intermediate value theorem -

De tussenwaardestelling (ook wel de stelling van Bolzano) zegt het volgende:

als een functie f continu is op interval [a, b],
en M is een getal tussen f(a) en f(b),
dan is er minstens één getal c te vinden zodat geldt;
• a < c < b
• f(c) = M

Wauw! Klinkt geweldig geleerd, vind je niet?

En toch schaam ik me er bijna voor om dit op te moeten schrijven.
Wat staat hier nou helemaal in "normaal Nederlands" ????

Eigenlijk helemaal niets!

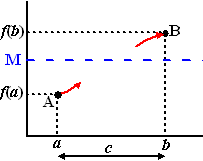
Er staat eigenlijk alleen dat je, als je in de figuur hiernaast van A naar B wilt gaan zonder je potlood van het papier te halen (continu), dat je dan ergens tussen a en b elke blauwe lijn M moet passeren (je mag je potlood alleen maar naar rechts bewegen (functie)).

In nog normaler Nederlands: "Als je van de ene kant van de grens naar de andere kant van grens wilt lopen, dan zul je de grens moeten passeren!"

Toepassing.

De meest voorkomende toepassing van de tussenwaardestelling is om aan te tonen dat een functie ergens nulpunten heeft.

Voorbeeld. Toon aan dat de functie f(x) = x³ - 2x²+ 5 een nulpunt heeft
tussen x = -2 en x = 0
Nou, f(-2) = -11 en f(0) = 5.
Omdat f continu is, worden tussen x = -2 en x = 0 alle waarden tussen -11 en 5 minstens één keer aangenomen, dus nul ook.

Om op te letten.
Twee puntjes van aandacht:

•

De tussenwaardestelling zegt dat elke waarde tussen f(a) en f(b) minstens één keer aangenomen wordt, dat kan dus ook best vaker zijn!

•

De tussenwaardestelling zegt niets over waarden die niet tussen f(a) en f(b) liggen.
Die worden misschien niet aangenomen, misschien wel, misschien zelfs vaker.... je weet het niet!


OPGAVEN

1.	We bekijken in deze opgave polynomen. Dat zijn functies van de vorm y = axⁿ + bxⁿ^{- 1} + cxⁿ^{- 2} + ...

	a.	Toon aan dat, als n een oneven getal is, deze polynomen minstens één nulpunt hebben.

	b.	Toon aan dat, als n een oneven getal is, deze polynomen een oneven aantal nulpunten hebben (daarbij wordt een meervoudig nulpunt als meerdere nulpunten geteld).

2.	Een vreemd treintje rijdt een traject van 1000 km. Maar dat gebeurt erg onregelmatig. Het treintje rijdt lang niet steeds even snel, stopt zelfs af en toe, en kan zelfs stukken achteruit rijden. Alles vrij willekeurig. Na afloop blijkt het treintje over het totale traject precies 20 uur gedaan te hebben. Dat betekent een gemiddelde snelheid van 50 km/uur. Bewijs dat er dan een stuk van 50 km moet bestaan waarover het treintje EXACT één uur gedaan heeft. (Hint: bekijk van alle mogelijke stukken van 50 km hoe lang het treintje erover heeft gedaan....)

3.	a.	Toon aan dat f(x) = 2x³ - 3x² + 5x - 10 een nulpunt heeft tussen x = 1 en x = 2

	b.	Toon aan dat lnx = √x - 2 een oplossing tussen x = 28 en x = 29 heeft.


© h.hofstede (h.hofstede@hogeland.nl)